定义2.1 由随机向量y的线性函数估计随机向量x,记估值为
其中,b与A为适维向量与矩阵。若估值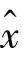 最小化性能指标
最小化性能指标
则称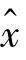 为随机变量x的线性最小方差估计,其中,E为均值算子。
为随机变量x的线性最小方差估计,其中,E为均值算子。
定义方差阵和协方差阵符号
Pxx=E[(x-Ex)(x-Ex)T] (2-11)
Pxy=E[(x-Ex)(y-Ey)T] (2-12)
易知有关系
Pxy=PTyx (2-13)
引理2.1 随机变量y对随机变量x的线性最小方差估值为
证明:将式(2-9)代入式(2-10)有
J=E[(x-b-Ay)T(x-b-Ay)] (2-15)
应选择b和A最小化J。置
这引出
b=Ex-AEy (2-17)
将式(2-17)代入式(2-15)得到
其中,符号tr表示矩阵的迹。应用矩阵迹求导公式
置∂J/∂A=0,有
利用关系式(2-13)引出
A=PxyP-1yy (2-21)证毕。
由于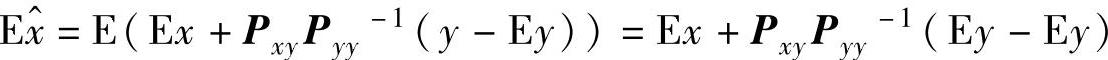 ,故
,故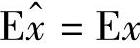 。这一性质称为无偏性。由于
。这一性质称为无偏性。由于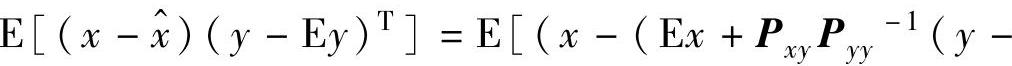
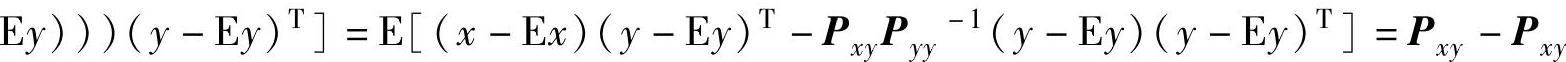
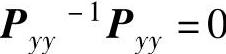 ,故
,故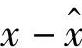 与y不相关。(https://www.xing528.com)
与y不相关。(https://www.xing528.com)
定义2.2 (见第1章)称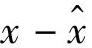 与y不相关为
与y不相关为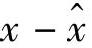 与y正交(垂直),记为
与y正交(垂直),记为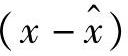 ⊥y,并称
⊥y,并称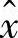 为x在y上的投影,记为
为x在y上的投影,记为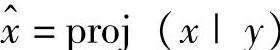 。
。
定义2.3 由随机变量y张成的线性流形定义为如下形式随机变量z的集合
以上线性流形的定义与第1章由span定义的空间有本质区别。由于(x-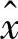 )⊥y,易知
)⊥y,易知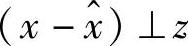 ,
,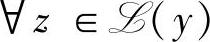 ,记为
,记为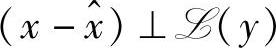 。
。
定义2.4 由随机序列y(1),…,y(k)张成的线性流形定义为
引入分块矩阵
则
定义2.5 基于随机序列y(1),…,y(k)对随机变量x的线性最小方差估计定义为
也称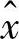 为x在线性流形
为x在线性流形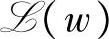 或
或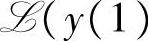 ,…,y(k))上的投影。
,…,y(k))上的投影。
引理2.2 设x为零均值随机变量,而y(1),…,y(k)为零均值、互不相关(正交)的随机向量,则可得
即x在由y(1),y(2),…,y(k)张成的线性流形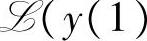 ,y(2),…,y(k))上的投影等于它在由每一个y(i)张成的线性流形上的投影之和,也即x在全空间上的投影等于它在相互正交的子空间上的投影之和。
,y(2),…,y(k))上的投影等于它在由每一个y(i)张成的线性流形上的投影之和,也即x在全空间上的投影等于它在相互正交的子空间上的投影之和。
证明:记合成向量w=[yT(1),yT(2),…,yT(k)]T,注意Ex=0,Ew=0,则应用式(2-14)有
证毕。
利用式(2-14)所表示的线性最小方差估值,则可得
proj(Bx+B′z|y)=Bproj(x|y)+B′proj(z|y) (2-28)
其中,B、B′为适维矩阵。
引理2.3 记x的分量形式为x=[x1,x2,…,xn]T。则有关系
即随机变量x在线性流形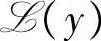 上的投影的每个分量必为x的相应的分量在线性流形
上的投影的每个分量必为x的相应的分量在线性流形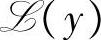 上的投影。换言之,在线性流形
上的投影。换言之,在线性流形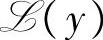 上,随机变量x的线性最小方差估计的每个分量等于x的相应的分量的线性最小方差估计。
上,随机变量x的线性最小方差估计的每个分量等于x的相应的分量的线性最小方差估计。
证明:利用式(2-14)所表示的线性最小方差估值,可得
证毕。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




