状态估计与开环预测技术简介

在某些应用问题中真实信号甚至被噪声淹没，滤波的目的就是过滤噪声，还原真实信号。这类问题广泛出现在信号处理、通信、目标跟踪和控制等领域。通常噪声、信号均为随机过程，因而滤波问题本质上是统计最优估计问题。从被噪声污染的观测信号中过滤噪声，求未知真实信号或状态的最优估值的过程也称为最优滤波。常用的最优估计准则是线性最小方差估计，即信号的最优估计与真实值的差的方差最小。

Kalman滤波是现代控制理论创始人之一R.E.Kalman在1960年提出的。该方法为时域上的状态空间方法，给出了一套递推滤波算法，便于在计算机上实时实现，具有计算量和存储量小的特点。在该方法中，信号被视为状态或状态的分量。20世纪60年代初，由于电子计算机运算速度和存储量的限制，要求存储量小、计算量小的滤波算法。满足这些要求的算法就是递推滤波算法。

下面以第1章测量长度为θ的物体为例来说明递推算法^[59]。记基于N个测量值对θ的估值为

当测量次数N不断增加，即进行动态测量时，基于N+1个测量值对θ的估值为

这种计算是非递推的，即彼此独立地计算估值和，有重复的加法运算，且当N增加时，计算量增加。为了减小计算负担，是否能在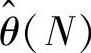基础上计算，这就是递推算法的思想。事实上，

即有递推公式

因而在估值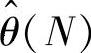的基础上，只需加上式（2-4）的第二项就可立刻得到估值+1），避免了非递推算法式（2-2）的重复加法运算。对于非递推算法，计算机需存储N个测量数据，而对递推算法式（2-4），不需存储过去的数据。式（2-4）中的第二项为校正量，它是根据差值

的大小来进行校正的。因为该差值包含了从第N+1次测量中去掉前N次测量的信息后剩下的新的信息，故称为“新息”（Innovation）。于是最终得到新息校正形式的递推估值公式

其中，K（N+1）＝1/（N+1）叫作新息校正系数或滤波增益。式（2-6）印证了Kal-man滤波的基本思想。(www.xing528.com)

Kalman滤波的基本特征和关键技术之一是状态空间模型，下面用如下启发性的例子来说明。

例2.1 动态测量系统Kalman滤波问题。

对未知长度为θ的物体进行动态测量，即测量次数k是变化的，k≥0。因长度θ为未知常数，故有θ的动态方程为

θ（k+1）＝θ（k） （2-7）

而第k次对θ的测量值l（k）含有随机误差ξ_k，故有对θ的观测方程为

l（k）＝θ（k）+ξ（k） （2-8）

可将未知长度θ定义为系统的状态，则式（2-7）称为状态方程，它描写θ随k变化的规律，式（2-7）说明长度θ不随k变化，即θ为常数。而式（2-8）则是对状态θ的观测方程，观测误差ξ（k）通常为白噪声。式（2-7）和式（2-8）构成最简单的状态空间模型。Kalman滤波问题：基于k+1次观测{l（0），l（1），…，l（k）}求θ的线性最小方差估值。它与θ的最小二乘估值不同的是：后者不需要已知观测误差ξ（k）的统计特性（均值和方差）。

在本书中，信号、状态估计需要解决的问题主要包含在双层结构预测控制的“开环预测模块”中。该模块采用可由Kalman滤波解释的方法进行不可测DV、状态和未来输出的估计。本书的主要研究中，预测控制基本上可以定义为“基于Kalman滤波/预报和滚动优化的最优控制”。将预测控制分为滤波/预报和最优控制两个阶段是很重要的观点，这使得众多的滤波算法（扩展Kalman滤波、无迹Kal-man滤波、信息融合估计、粒子滤波等）可以和各种最优控制方法相结合，得到预测控制。本章的主要参考文献是参考文献[59]。