动态模型与稳态模型详解

在MPC的应用过程中，涉及过程的稳态模型和动态模型，其中稳态模型将用于稳态目标计算，动态模型用于动态控制。

例1.3 （见参考文献[95]）以一个简单的传热过程为例来说明稳态模型与动态模型之间的关系。假设传热过程的动态数学模型为

式（1-36）中，T为温度输出，Q为可控的热量输入，T_i为温度干扰，V、ρ、C、w为体积、密度、比热容、质量流量。如果该过程达到稳态，则应将式（1-36）的左端的微分项置零，相应的稳态模型为

wC（T_i-T）+Q＝0

由此可见，稳态模型可由动态模型得到。

稳定CV有稳态值，积分CV则有稳态斜率值。

例1.4 （见参考文献[95]）以一反应器的液位系统为例来说明积分过程。如图1-6所示，系统具有三个阀、一个计量泵。通过泵的流速是恒定的，即反应器的流出量与反应器液位的高度无关。反应器的液位相对于v1、v2和泵这三个系统输入量呈现积分特性，因此必须合理地控制v1、v2和泵的流量才能保证液位的稳定。泵的流速u和液位y之间的关系可以表达为

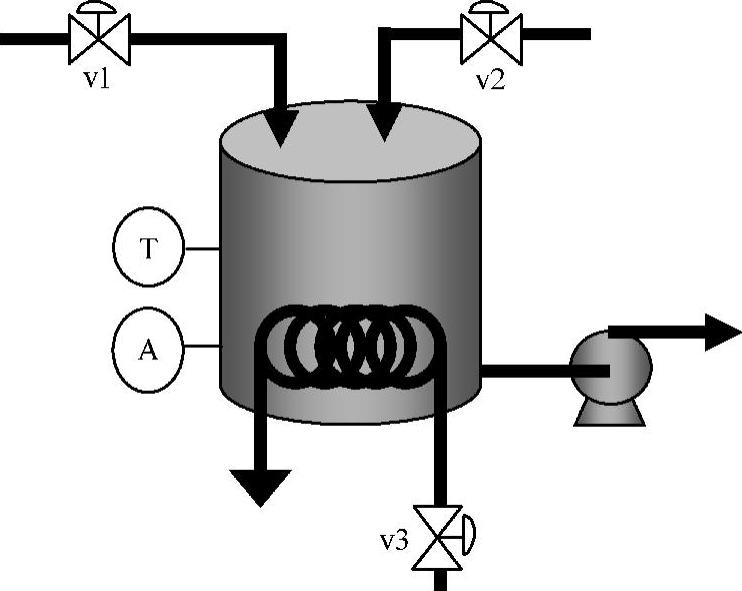
图1-6 反应器的液位系统示意图(www.xing528.com)

式（1-37）的意义为输出变量y的变化率与输入变量u的比值为一常数。将式（1-37）进行离散化处理，可得

当u达到稳态后，y（k）-y（k-1）的值也达到稳态，即在单位采样周期内上升或下降的垂直距离恒定。

在本例中，如果将流量泵更换为负载阀，则反应器的液位相对于v1、v2呈现稳定过程特性，原因在于负载阀类似于一个液阻，具有自平衡能力。

例1.5 （见参考文献[95]）以一简单传递函数为例。选定u（t）＝1，即输入u（t）为单位阶跃函数，过程的输出响应如图1-7所示。可见，在一定时间后，输出的变化率到达“稳态”。

由FSR的模型特点可知，稳态响应时间（settling time或time to steady state）是开环稳定过程一个非常重要的参数——如果过程受到阶跃（或脉冲）MV或DV的作用，CV将在稳态响应时间内达到稳态。对积分CV，稳态通常针对变化速率。

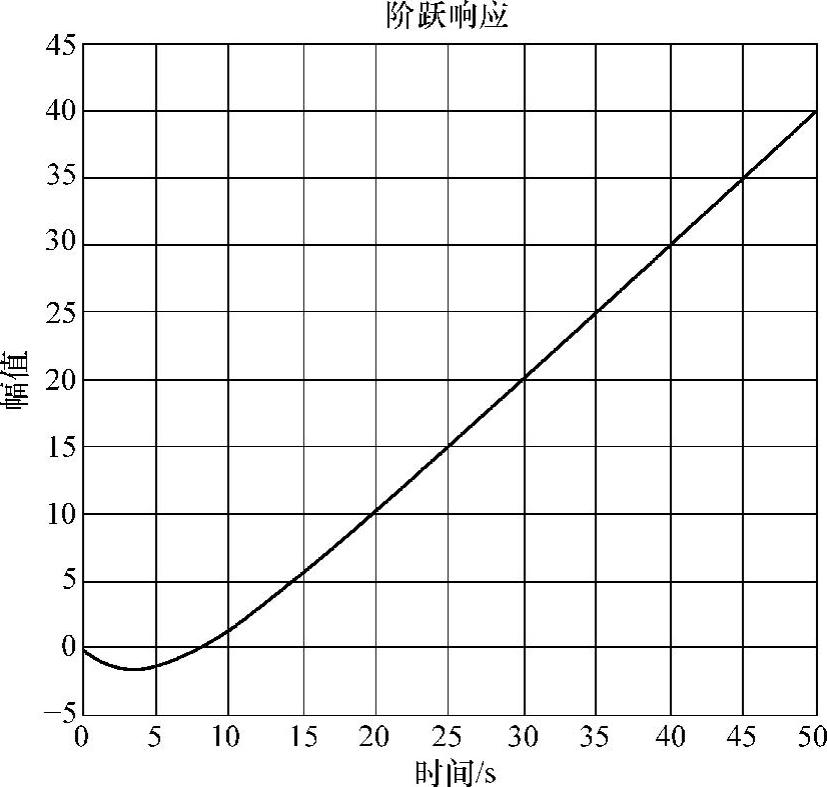
图1-7 积分过程的单位阶跃响应