工业预测控制的数学模型优化

为了实现工业过程的动态优化控制，需要建立工业过程的相对精确的数学模型。直接的方法是研究工业过程的机理（白箱，white box）模型，但这非常困难，因为大多数工业过程的机理都很复杂。如果只关心过程的外特性，即把过程看作是黑箱（black box），根据过程的输入输出数据信息，辨识得到等价的外特性模型则相对容易得多（见图1-3）。正因为如此，大多数的MPC控制策略均通过辨识方法得到工业过程的数学模型，将之作为控制器的核心部件内置于控制器中。MPC是一种复杂工业过程控制和优化的有效手段，但前提是要得到相对准确的工业过程数学模型。获取工业过程的数学模型是MPC实施过程中最困难的阶段。

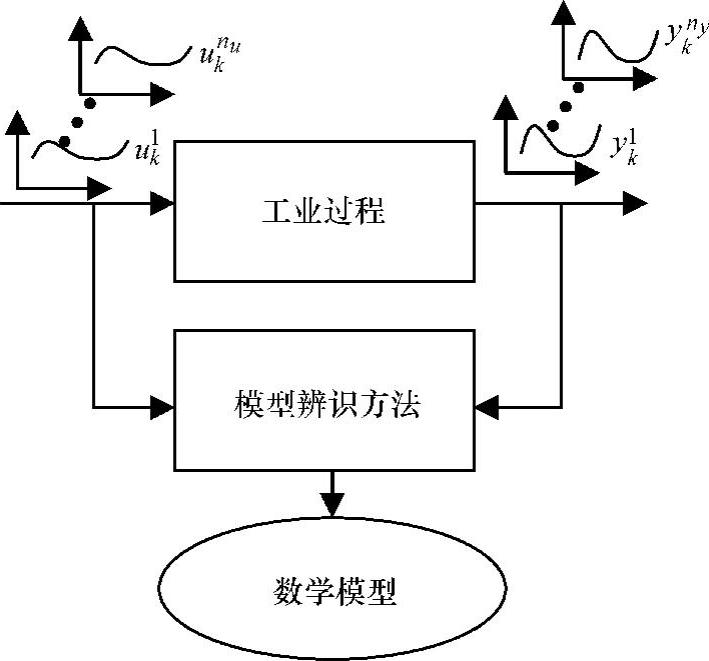
图1-3 模型辨识的基本含义(www.xing528.com)

实际的工业过程都是非线性的，线性是相对的。常规情况下，生产过程运行在系统的稳态工作点附近，但这些稳态工作点并不是随意选取的，而是满足系统稳态关系条件（即稳态模型）的点的集合，该点集可形成平衡面。并非所有的非线性系统都存在平衡面，但对于大多数的工业生产过程，平衡面是存在的。

平衡面中的每一个点理论上都可以作为系统的平衡点。但在实际生产过程中，生产的目标是使经济效益最大化，而且每个变量都有期望的约束条件，这时运用优化理论可以得到最佳的平衡点。作为最有效的多变量控制手段，MPC的作用就是使多变量控制系统运行在最佳的平衡点上。对于流程工业自动化，大多数的生产过程在平衡点附近可以看作是线性的，并可以按照线性系统的建模与控制方法处理，但某些生产过程的非线性非常强，这时线性系统的理论则不适宜，应采用非线性建模与控制方法。