随机过程的均值和自相关函数及其应用

本小节部分内容参考了参考文献[60]。随机过程的两个最基本的数字特征是均值和自相关函数。如果一个随机过程的统计性质不随时间改变，则称它为平稳随机过程。在实际应用中，往往对“统计性质”的了解局限到均值和自相关函数这两个数字特征上，这意味着放松了对于平稳性的要求，从而提出了“宽平稳随机过程”的概念。本书的平稳随机过程都是指宽平稳随机过程。对一个平稳随机过程，均值和自相关函数有“一个样本集合的平均值”和“很长一段时间的平均值”之分。如果这两种平均值是相等的，则称该平稳随机过程为各态历经的。本书后面讨论的随机过程都是指各态历经的平稳随机过程。

对各态历经的平稳随机过程，标量点列{v（k）|k≥0}的均值和自相关函数可计算为

如果v为向量，则其不同分量v_i和v_j的互相关函数可计算为

与以上概念对应，方差函数、协方差函数和互协方差函数定义为

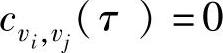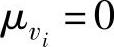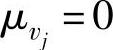若，∀τ∈（-∞，∞），则称v_i（k）与v_j（k）互不相关（或不相关）。若或者，则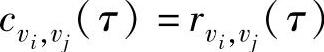。当L有限时，得到相应的样本估计结果。比如：

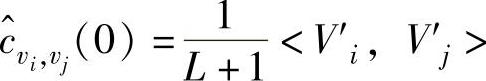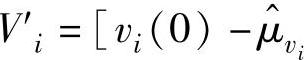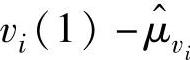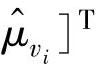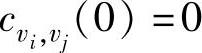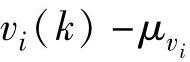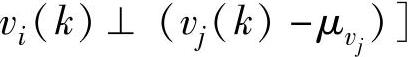特别地，，其中，，…，v_i（L）-，因此若，则称和v_j（k）正交（或者垂直），记为（v_i（k）-[同理，。(www.xing528.com)

考虑各态历经的平稳随机过程，对n维实空间中的两个点列{v（k）}和{w（k）}，其中v（k）和w（k）都是列向量，定义互协方差阵

如果C_vw（τ）＝0，∀τ∈（-∞，∞），则称v（k）和w（k）不相关，这是前面不相关定义的推广。相应地，C_vv（τ）定义为v（k）的协方差阵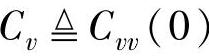；定义为v（k）的方差阵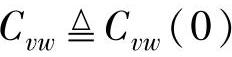；定义为v（k）和w（k）的协方差阵。这些矩阵的命名是按照对角线元素的。特别地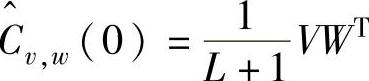，，其中V＝[v（0），v（1），…，v（L）]，W＝[w（0），w（1），…，w（L）]，因此若C_vw＝0，则称v（k）-μ_v和w（k）正交（或者垂直），记作（v（k）-μ_v）⊥w（k）[同理，v（k）⊥（w（k）-μ_w）]，并称μ_v为v（k）在w（k）上的投影，记为μ_v＝proj（v（k）|w（k））。

确定性过程的正交、垂直、投影的概念与随机过程的相应概念是一致的。

此外，在模型辨识或对辨识结果进行分析时，很多情况下都会用到平均功率谱密度的概念。某个信号在某个频率处的平均功率谱密度表示该频率的能量的“无限时间平均”，简称谱密度。谱密度函数是谱密度与频率的关系方程。令v（k）为一平稳随机过程，则其谱密度函数ϕ_v（ω）与自相关函数r_v（τ）构成了一组傅里叶变换对，即

称为Wiener-Khintchine公式，其中ω为频率。令w（k）为另一平稳随机过程，定义w（k）与v（k）的互谱密度为