确定性过程中向量组的张成空间及伪逆

本小节部分内容参考了参考文献[88]。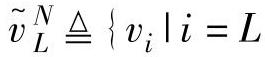，L+1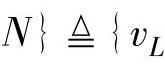，…，，v_L+₁，…，v_N}∈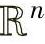表示n维实向量空间中的向量组，其中，v_i可以是行向量或者列向量。所谓由n维实向量组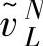张成的空间，记为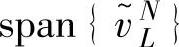，是指包含所有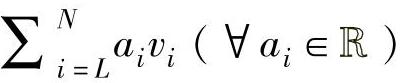的n维实空间的子空间。对一个矩阵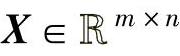，其行空间是指由X的行向量张成的空间，列空间是指由X的列向量张成的空间，故行空间是n维实空间的子空间，列空间是m维实空间的子空间。当X行满秩时，列空间等于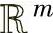；当X列满秩时，行空间等于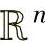。由于一个矩阵X∈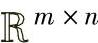总可以表示一个m维实空间的子空间和一个n维实空间的子空间，因此X总是某些子空间的表示矩阵。一个子空间的表示矩阵不是唯一的，但是所有表示矩阵在表示该子空间的意义下应是等价的。

对n维实空间的两个列向量{v_i，v_j}，称＜v_i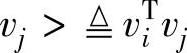，为v_i与v_j的内积；如果＜v_i，v_j＞＝0，则称v_i与v_j正交（或者垂直），记为v_i⊥v_j。相互正交的非零向量必是线性无关（或线性独立）的。对n维实空间的两个子空间{X，Y}，如果X的任一向量与Y的任一向量的内积都为零（如针对行向量的情况，XY^T＝0），则称X与Y正交（或垂直），记为X⊥Y；X的正交补空间，记为X^⊥，是指所有与X正交的向量张成的空间。如果X是列空间的表示矩阵，则（X^⊥）^TX＝0、X^T（X^⊥）＝0。如果X是行空间的表示矩阵，则（X^⊥）X^T＝0、X（X^⊥）^T＝0。

一个n维实向量v在n维实空间的子空间X上的投影，记为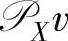，是指X上距离v最近的点，即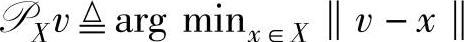，其中符号‖·‖表示Euclidean范数（向量元素二次方和的开方值）。由于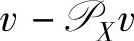与X上的任一向量都正交，即（v-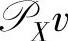）⊥X，这里的投影也经常称为正交投影。一个空间在另一个空间上的投影的定义是以上投影定义的推广，将在子空间辨识一章描述。

对任意X∈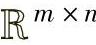（m≥n，X^TX可逆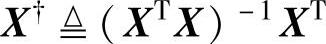），称为X的左伪逆。对任意X∈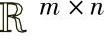（m≤n，XX^T可逆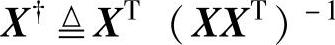），称为X的右伪逆。左伪逆和右伪逆统称为Moore-Penrose伪逆。(https://www.xing528.com)

分块矩阵求逆公式：如果A、B、ΔA-DB^-1C均为适维非奇异矩阵，则

奇异值分解（Singular Value Decomposition，SVD）：对任意实矩阵A，总可以表示为A＝QVR，其中，{Q，R}为正交方阵（Q^TQ＝I、R^TR＝I）、V为与A同样维数的对角矩阵。V的对角线元素为奇异值，从左上开始向右下逐渐减小。