预测控制的优化变量选择

一般工业过程的输入输出结构如图1-1所示。工业过程的输入通常可分为两类，一类是可控输入（控制输入），也称为操作变量（Manipulated Variable，MV）；另一类是不可控输入，即干扰变量（Disturbance Variable，DV），包含可测干扰和不可测干扰。动态控制的目的就是克服DV的影响，并使被控变量（Controlled Var-iable，CV）具有期望的动态特性。对于可测DV，在其到CV的模型已知的前提下即可通过前馈加以补偿，故可测DV有时也称为前馈变量（FeedForward variable，FF）。但是，对于不可测DV，只有其作用到被控过程并反映出来后，才能通过反馈方式抑制其影响。

变量选择就是确定MV、DV和CV。

典型的MV包括回流流量、再沸器流量或热负荷、压缩机转速等。MV通常为常规底层控制回路（PID为主）的设定值，如果过程动态过于缓慢，则可使用阀位作为MV，但要考虑阀的非线性问题。MV的数量受限于实际系统的可自动调节的阀门等执行机构的数量。

典型的DV包括进料流量、进料温度、进料组分等。要尽量将所有的可测DV都包含在控制器设计中，即便它们在另一单元或DCS系统。

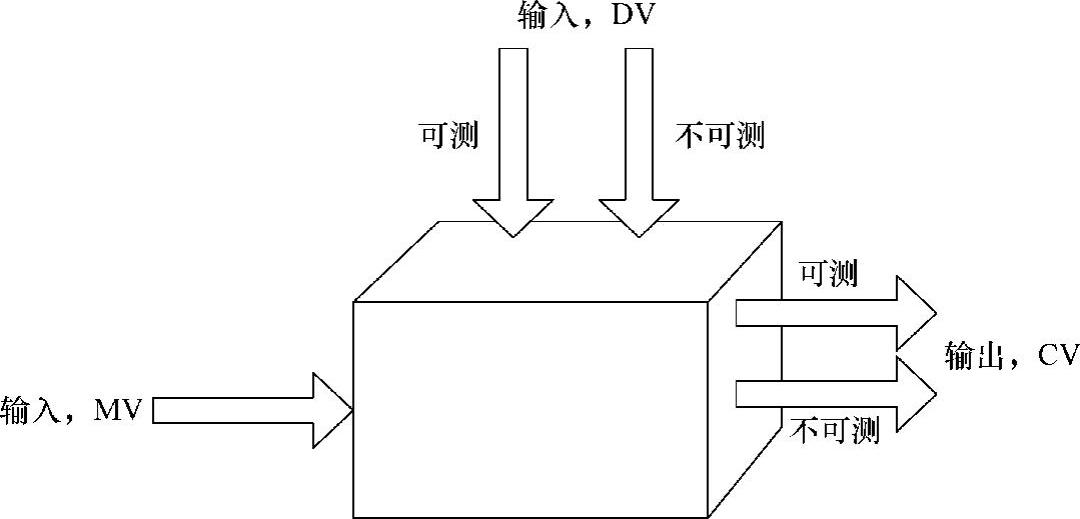
图1-1 工业过程的输入输出结构

典型的CV包括流量、液位、温度、压力、成分等。对同一个变量，其真实值可以作为CV，而其PID设定值可以作为MV，该PID对应的阀门开度也可以作为CV。MPC中某些CV可能没有跟踪设定值的要求，只要处于一定的范围内即可。CV分可测与不可测两种，本书仅考虑可测CV，不可测CV的处理可能涉及软测量等技术。通常，CV的个数不等于MV。(www.xing528.com)

若系统进入稳态后，对输入做一阶跃变化，某CV在一段时间后重新进入到新的稳态，则称此CV为稳定（Stable）CV。若系统进入稳态后，对输入做一阶跃变化，某CV经过一段时间后保持匀速上升或匀速下降，则称此CV为斜坡（Ramp）变量或者积分CV。在MPC的工程实现中，一般可设定积分CV与所有输入之间呈现积分特性。

如果一个变量不受被控过程中其他变量的影响，则称其为独立变量（Inde-pendent Variable，IndepV），反之称为依赖变量（Dependent Variable，DepV）。故IndepV的任何改变都来自被控过程之外，如由控制器改变MV、人扳动阀门等。MV和DV都是IndepV，而CV一定是DepV。IndepV不限于MV和DV，DepV也不限于CV。不可能所有的IndepV都作为MV和DV，更不可能所有的DepV都作为CV。对一个实际工业过程，MV、DV、CV的选择要兼顾操作的平稳性、安全性及经济效益的优化等，故是一个复杂的问题，就像医生诊断病情一样，不可能有统一的定律。

以一个分馏塔顶温度、回流流量组成的环节为例。可以选择回流液阀门开度作为MV，而回流流量和塔顶温度为CV。如果采用了PID控制回流流量，则可以选择回流流量PID的设定值作为MV，而回流流量和塔顶温度及阀门开度都可作为CV。如果采用了串级PID控制塔顶温度，温度PID为主回路、流量PID为副回路，则可以选择塔顶温度PID的设定值为MV，而回流流量和塔顶温度及阀门开度都可作为CV。这些就像医生采用了不同的治疗方案一样，药方也会随之不同。

在具体的预测控制工程实现中，移除一些原有的组态、增加一些原来没有的底层控制组态、重新整定PID控制回路等，都是可能需要做的工作。这些工作的主要作用是使预测控制的被控系统呈现更“容易控制”的动态特性（如线性特性）。这些工作与控制算法的功能（是否有积分处理、是否有非线性变换）、模型辨识方法、控制结构选择、具体工艺流程（响应速度、安全性）等都有关系，是个无限可延伸探讨的话题。

对于具体的系统模型，输入通常指IndepV，输出通常指DepV，比如：多变量系统指多于一个IndepV和/或多于一个DepV的系统；多入多出系统表示多于一个IndepV、多于一个DepV的系统。