如何估算流体流动阻力？

任务目标

知识目标

1.了解流动阻力产生的原因。

2.掌握不同类型流体流动阻力的估算方法。

3.掌握管路流体流动总阻力的估算方法。

技能目标

掌握减小流体流动阻力的方法。

任务描述

通过对管路阻力的估算，找到减小流体流动阻力的方法。

知识学习

一、流体稳态流动时的物料衡算——伯努利方程

当流体在流动系统中作稳态流动时，根据能量守恒定律，对任一段管路内流体流动作能量衡算，即可得到表示流体的能量关系和流动规律的伯努利方程。

1.流体定态流动时能量形式

在图4-28所示的稳态流动系统中，流体从截面1—1流入，经管道从截面2—2流出，管路上装有对流体做功的泵。

衡算范围：1—1与2—2截面间内壁面。

衡算基准：1kg流体。

基准面：O—O平面。

1kg流体进出系统时输入和输出的能量有流体的机械能、功和能量损失。

（1）流体的机械能 包括位能、压强能和动能。

图4-28 能量衡算

1）位能。流体因受重力作用，在不同高度处所具有的能量相当于将流体从基准面提升距离z所做的功。1kg流体的位能=gz。位能是相对值，在基准面以上为正值，基准面在以下为负值。

2）压强能。流动流体的内部任一位置都有其相应的压力。若在充满液体的管路内，液体以一定的流速u流过，若在管壁处开一小孔，并与一根垂直玻璃管连接，可以观察到液体会在此玻璃管内上升至某一高度，此液柱高度表示小孔管壁处压强的大小。对于图4-28所示的流动系统，流体通过截面1—1时，由于该截面处流体具有一定的压力，即流体通过1—1截面必定要带着与所需的功相当的能——静压能，才能进入系统。

。

3）动能。流体以一定的流速流动时所具有的能量称为动能。。

位能、动能和静压能均为机械能，三项之和统称为总机械能。此外图4-28中管路还安装泵，则进出系统的能量还有流体与外部的能量交换。

（2）功 功是指1kg流体通过泵（或其他输送设备）所获得能量的W_e，其单位为J·kg^-1。

（3）损失能量 流体流动时因克服摩擦阻力而消耗的部分能量称为损失能量。这部分能量在流动过程中转化为热，散失于周围的环境中或使流体温度略有升高，由于这部分能量不能回收而损失掉了，损失能量用符号∑W_f表示，其单位为J·kg^-1。

损失能量应列入输出系统的能量。

2.流体稳态流动时的机械能衡算式——伯努利方程式

在图4-28所示的稳态流动系统中，通过能量衡算，可以得出流体流动时的伯努利方程式。衡算范围为1—1至2—2截面之间。

式中，p_e=ρW_e，p_f1—2=ρ∑W_f1—2

式（4-23c）称为流体作稳态流动时的机械能衡算式。流体在一般输送过程中，多数情况下均为不可压缩流体——液体。因此下面着重讨论液体输送时的情况。

1）理想流体的伯努利方程式。理想流体是指流体在流动过程中不发生能量损失。理想流体的特征是：密度不随压力而变化，没有内摩擦力，不具有黏性，流动时无阻力。实际上生产实际中并不存在真正的理想流体。若理想流体无外加能量，则：

式（4-23d）称为理想流体的伯努利方程式。式（4-23d）说明理想流体在作稳态流动，又无外功输入时，每千克流体在任一截面所具有的总机械能E恒为常数，而每一截面上的不同机械能形式的数值却不一定相等。各种形式的机械能可以相互转换，如某流体在水平变径管道作稳态流动，流体在细管中流动时，由于流速增大，使动能增加，但总机械能E保持常数，则静压能相应降低；反之，在粗管中流动时动能减少，静压能则相应增加。

2）伯努利方程式中的外加能量是确定输送机械功率的重要依据。在单位时间内输送机械对流体所做的有效功称为有效功率，用N_e表示，单位为J/s或W。

N_e=q_mW_e=q_mhg （4-24）

式中 q_m——质量流量（kg/s）。

3）若系统中的流体处于静止状态，则u=0，流体不流动没有阻力，也不需要外加能量，即W_e=0，∑W_f=0，故

式（4-24）为静力学方程，可见伯努利方程式也可反映静止流体的基本规律，流体静止状态是流动状态的特殊情况。

二、流体流动阻力

流体流动会产生阻力，而流体的黏性（内摩擦力）是产生阻力的内因，流动状况是产生流体阻力的外因。要克服阻力，必须消耗一部分能量，故伯努利方程式在实际应用中有能量损失这一项。

流体流经直管和管路附件（管件阀件等）的能量损失可分成直管阻力和局部阻力两类。

1.直管阻力

由理论推导可得到直管阻力计算的表达式：

从式（4-26a）～式（4-26c）中可见，流体在直管中的阻力损失或压头损失与摩擦因数λ、管道长度l、流速u及管道内径d密切相关。而摩擦系数λ是雷诺数Re和管壁粗糙度ε的函数，其值由实验测定，如图4-29所示的关系。

图4-29 摩擦系数λ与雷诺准数Re、相对粗糙度ε/d的关系

（1）圆形管

1）层流时的摩擦因数。从图4-29可见，当Re≤2000时，摩擦因数λ与雷诺数Re成直线关系。实验证明，层流时λ只与Re有关，而与管壁粗糙度ε无关。圆形直管在层流时的摩擦因数λ可用下式计算：

2）湍流时的摩擦因数。流体在湍流流动时的情况比层流复杂得多，摩擦因数与雷诺数和管壁粗糙度有关。工程上为了方便起见，一般都在手册上查取摩擦因数数值。从图4-29中可查湍流时的摩擦因数。

在化工生产所用的管道中，通常把玻璃管、黄铜管、铅管、塑料管等称为光滑管；把钢管和铸铁管等称为粗糙管。这样粗略地划分光滑管与粗糙管，从而为应用图4-29提供了方便。

3）过渡区的摩擦因数。过渡区是一种不稳定的流动形态，计算阻力时将过渡区视为湍流，按湍流时的曲线延伸出去查取摩擦因数的值。

（2）非圆形管 在生产实际中，有时会遇到流体在非圆形管（如方形管、套管环隙等）内流动，此时仍可用圆管内的式4-25a～式4-25c，但式中的d和雷诺数中的d必须用一个与圆管直径相当的量来进行计算，这个相当的量称为当量直径，用符号d_e表示。

式中 A——流道的截面积（m²）；

C——润湿周边长度，即流体与壁面接触的周边长度（m）。

例如，外管内径是D，内管的外径是d₀组成的同心圆套管环隙的当量直径为：

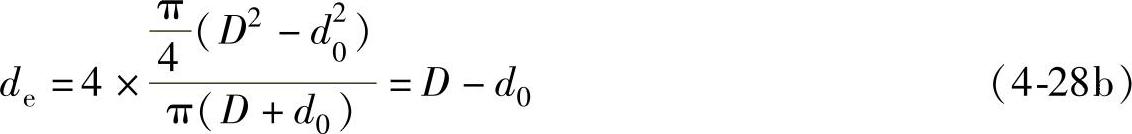(www.xing528.com)

边长分别为a和b的矩形管当量直径是：

【例4-8】 20℃的硫酸在1″的钢管中以0.2m/s的流速流动，管长100m，试求阻力损失和压力降。若同样流速下流动的是水，则阻力损失和压力降又是多少？

解：1.查20℃时硫酸，μ=23mPa·s，ρ=1831kg/m³

1″管子规格ϕ33.5mm×3.25mm

d=33.5mm-2×3.25mm=27mm

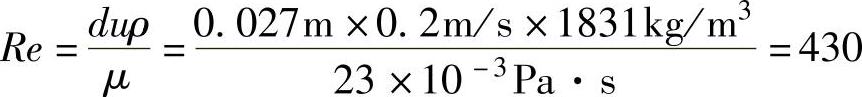
此流动属于层流

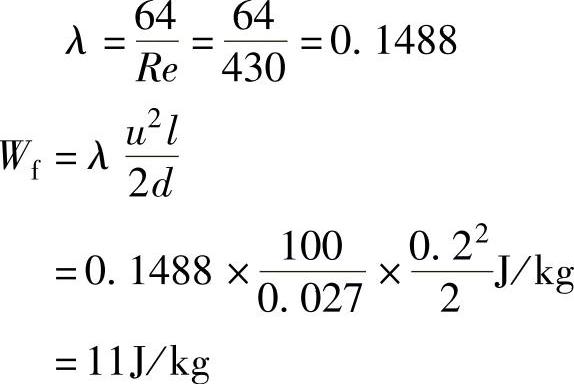
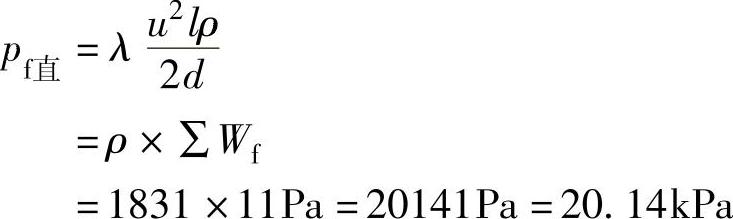
2.查20℃时水，μ=1.005mPa·s，ρ=998kg/m3

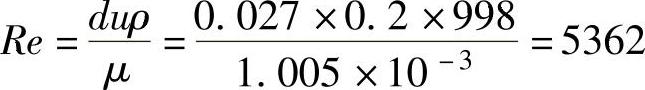
此流动属于湍流，查图4-29得：λ=0.042

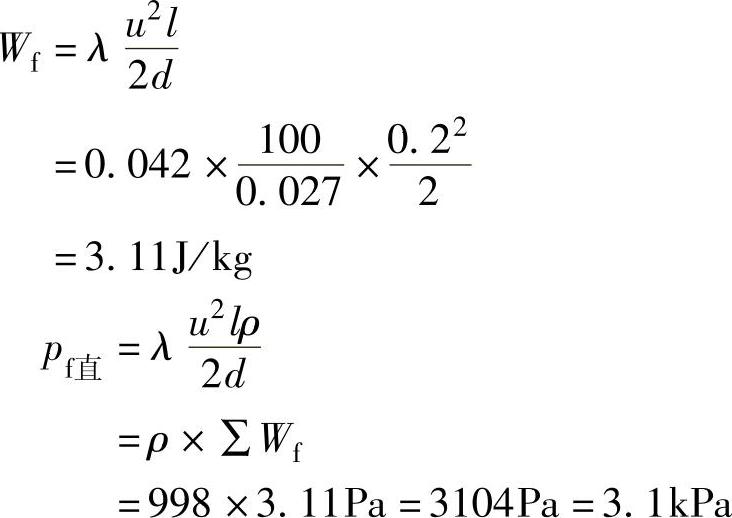
2.局部阻力

流体经过管道上某些局部位置，如弯头、阀门、管道骤然缩小或扩大时，流体的流速或流向突然发生变化，出现涡流并加剧湍动，使这些局部位置处的阻力显著增加。湍流时的局部阻力有两种计算方法。

（1）当量长度法 将局部阻力折算成相当于同管径直管长度所产生的阻力，此折算的管道长度称为当量长度，用符号l_e表示。l_e值由实验测定，在化工手册中查找使用，可以将其并入直管长度一起计算总的损失能量。

局部阻力

管路总损失能量（或压头）：

或

（2）阻力系数法 克服局部阻力引起的能量损失，还可以动能的倍数来表示，即局部阻力

管路总损失能量：

或

当流体流经的截面发生变化时，直管阻力应按不同的管径分段计算；计算管道突然缩小或扩大时的局部阻力，宜用小管内较大的流速值。

局部阻力计算比较繁琐，误差较大，用不同的方法计算的结果也有差异。作近似估算时，对不是很复杂的管路系统，局部阻力可估计为直管阻力的30%～50%。

3.降低流体阻力的途径

生产上流量一定时，将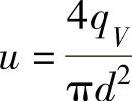代入式（4-29a），整理后得：

湍流时λ值变化不大。由式（4-31）可见，当管径增大一倍时，则阻力损失变为原来的1/32，动力消耗将大为减少。所以适当增大管径，对大流量的输送是很重要的，特别对低压气体在真空管路中输送尤为重要。

降低流体阻力可以从以下几个方面着手：

1）在符合生产管路布置的基本要求下，管路长度尽量缩短。

2）在具体的某个化工车间或装置内部，管路中的局部阻力占有相当大的比重，因此，对管路中设置的管件或阀件要慎重考虑，并设法降低其阻力系数。当管路的截面突然发生改变时，也要考虑将截面逐渐扩大或缩小，因为它可使阻力损失的能量降到原来的10%～20%。

3）适当增大管径。因为阻力损失与d⁵成反比，这样就使流体的阻力和动力消耗量大大地降低。

4）在流体中加入某种适宜的“添加剂”，使流体的压力降低，即降低流体的阻力主要是由于“添加剂”的存在，使管壁附近流体层流厚度增大，以及有阻碍旋涡产生的作用，而使摩擦因数λ值降低，从而使阻力损失下降。

目前使用的添加剂有可溶性高分子聚合物、皂类溶液及适当大小的固体颗粒稀薄悬浮物。

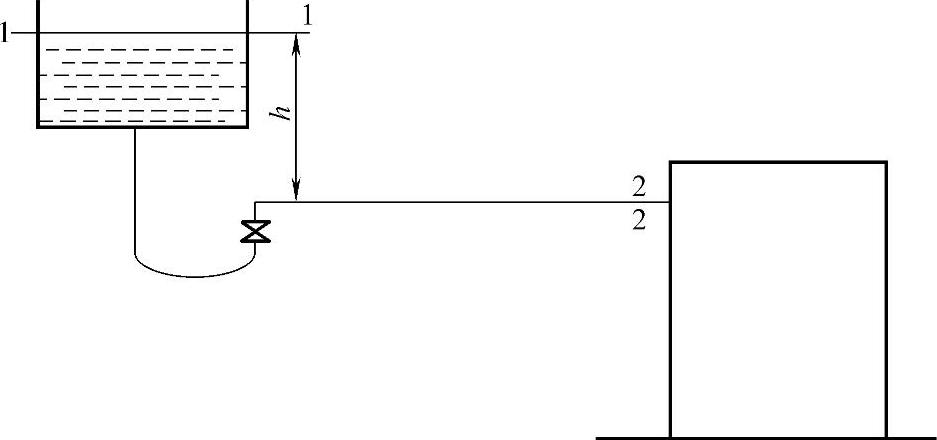
图4-30 例4-9附图

【例4-9】 用高位槽使料液自动流入精馏塔中，要求塔内连续稳态进料。高位槽液面保持恒定，塔内操作压力（表压）为0.4at，塔的进料量为50m³/h，已知料液密度为900kg/m³，黏度为15mPa·s，接管规格为ϕ108mm×4mm钢管，长度为9m，管路有一个180°回弯管，90°弯头一个，截止阀一个，则高位槽的液面要高出塔的进料口多少米才能达到要求？

解：取高位槽液面为1—1截面，如图4-30所示，塔进料管口为2—2截面，以2—2管中心线为基准水平面，在1—1面与2—2面之间列伯努利方程：

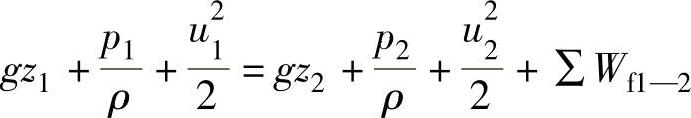
已知：z₁=h，u₁=0，p₁（表）=0，z2=0，p2（表）=0.4at d=108-4×2mm=100mm=0.1m

则

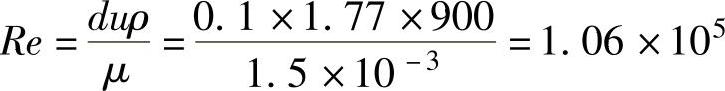
此流动属于湍流。查图4-29得λ=0.022。

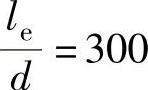由化工手册查得：储槽入口管，180°回弯管，90°回弯管，截止阀，则。

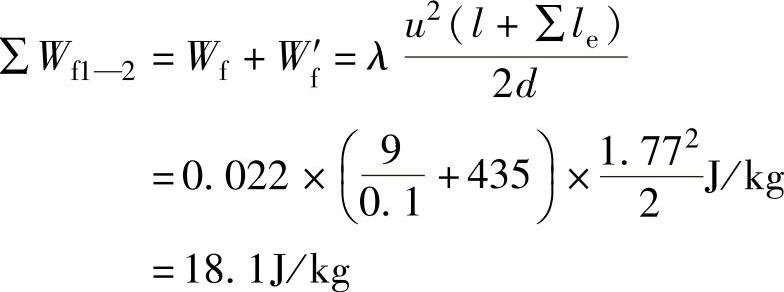
故

则，h=63.3/g=63.3/9.8m=6.45m

为保证所需要的流量，并考虑适当的调节余地，可取高位槽液面高出塔进料管口7m。

任务实施

1）用多媒体课件讲解流体流动阻力产生的原因及其估算方法。

2）用“拼图教学法”让学生进行简单管路的计算。

3）用“滚珠教学法”让学生进行交流与考核。

任务评价

任务评价见表4-8。

表4-8 任务评价

（续）