识图过程中,对一些物体的形状由较完整的形体组成,或者物体的外形轮廓是完整的视图,用形体分析法就可以解决。但对一些经过切割、形状不规则或结构的投影关系相重合的视图,用形体分析法就很难看懂了。此时应采用线、面分析法来分析物体的表面形状和位置,并借助立体概念综合想象出物体的形状。
线、面分析法就是运用线、面的投影规律,把视图中的线框认定为物体上的面,把线认定为物体上的线或面。
根据已知视图的特点,一般将线、面分析法分成三种空间思维方法。
1.面组装法
识图时,先将视图中线、线框所表示的面的形状和相对位置确定下来,再将这些面进行组装想象,综合想象出物体的形状。
例5-17 如图5-40a所示,已知主、左视图,求作俯视图。
1)确定各面的形状和空间位置。主视图中线框a′对应左视图上斜线a″,则线框a′表示前、后两个梯形侧垂面,如图5-40b所示。
左视图中线框b″对应主视图中两条斜线段b′,则线框b″表示左、右两个三角形的正垂面,如图5-40c所示。
主视图中线段c′对应左视图中线段c″,但不能确定其表示的是线或是面,此时,可借助前、后和左、右侧面所围成的立体形状进行判断,确定线段c′和线段c″表示矩形水平面;线段d′对应左视图的投影为点,表示侧垂线,是前、后面A的相交线,如图5-40d所示。
2)综合想象整体。将左视图归位,根据视图关系想象出各表面的相对位置,如图5-40e所示,最后综合起来想象出整体形状,如图5-40f所示。
3)补画左视图。求作左视图时,将物体上的五个表面分别向水平面投影。面A为侧垂面,水平投影为类似形线框a;面B为正垂面,水平投影为类似形三角形线框b;面C为水平面,水平投影为矩形线框c。画图时可利用点、线的投影规律作图,如图5-40g所示。
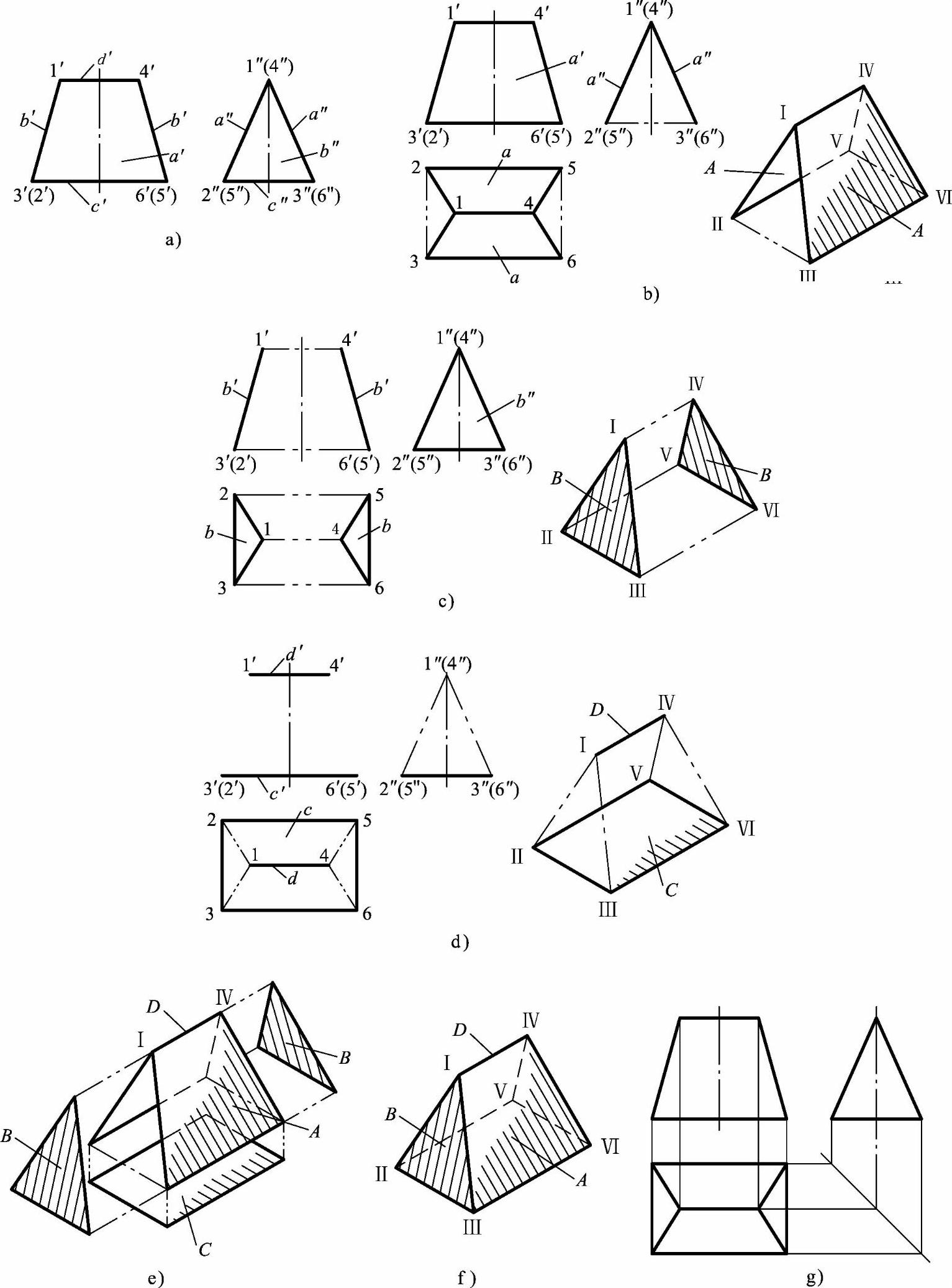
图5-40 线、面分析法
例5-18 如图5-41a所示,已知主、俯视图,想象立体形状,补画左视图。
1)分离线框。把主视图和俯视图分成若干个线框,并找出各自的对应关系。主视图中线框分为c′、d′、e′、f′,并分别找出其对应在俯视图中的投影关系;将俯视图中的线框分为a、b、(g),并分别找出其对应在主视图中的投影关系。
2)根据各线框对应投影关系,想象出线框所示平面的形状和空间位置。
俯视图中线框a、b在主视图中无类似形线框对应,表示特殊位置平面,对应主视图投影分别为横向线a′、b′,线框a、b均表示水平面,面A高,面B低,其侧面投影均为横向线a″、b″,如图5-41b所示。
主视图中线框c′、d′、e′、(f′)对应在俯视图中无类似形线框,表示特殊位置平面,其分别对应俯视图中横向线段c、d、f和斜线段e;线框c′、d′、(f′)分别表示正平面,面D在前,面C在中间,面F在后,其侧面投影均积聚成竖向线;线框e′表示铅垂面,侧面投影为类似形线框,如图5-41c所示。
俯视图中线框(g)对应主视图中线段g′,表示水平面,其侧面投影积聚成横向线。
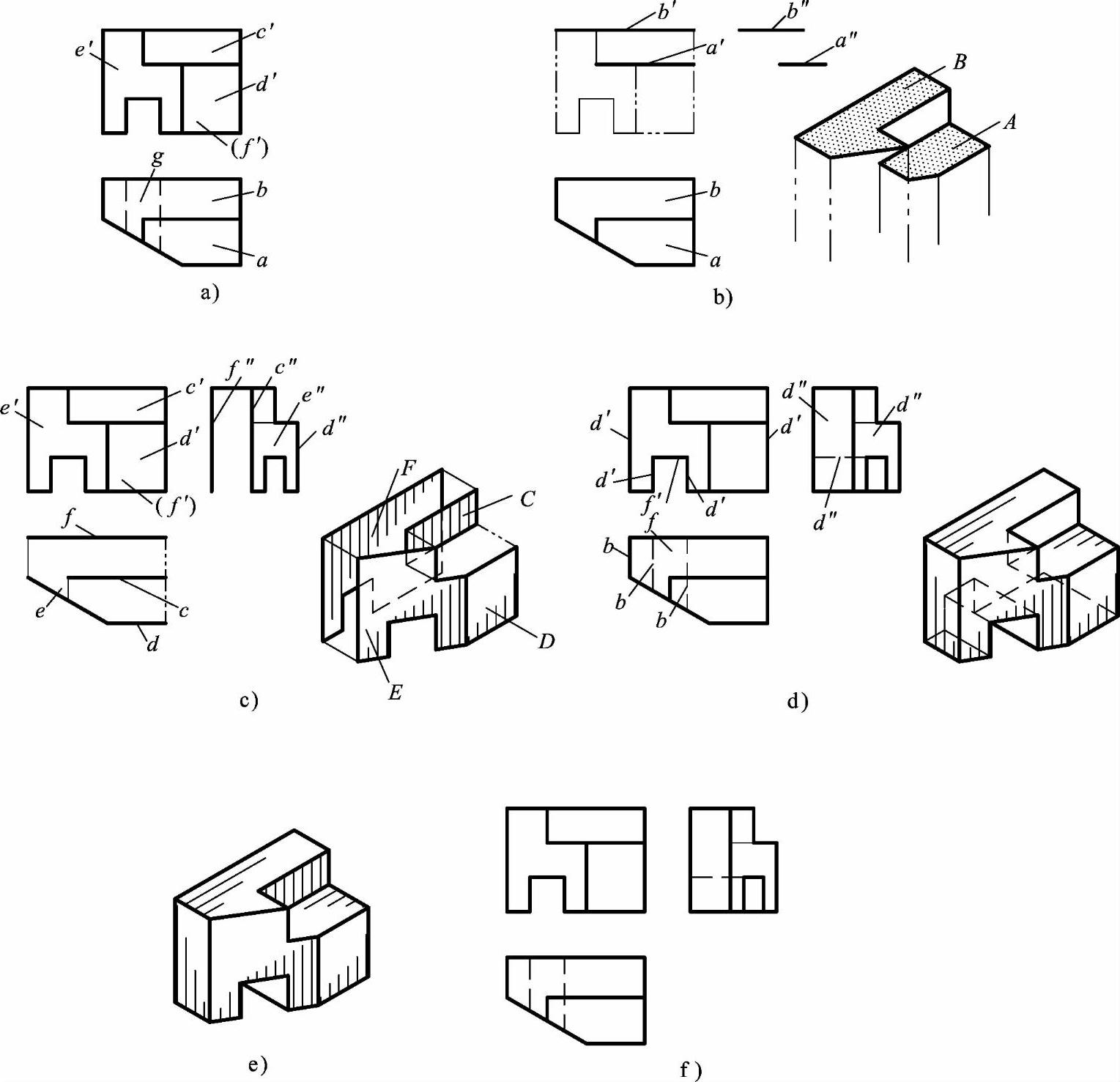
图5-41 已知主、俯视图,补画左视图
3)综合起来想象立体形状。通过上述的投影分析后,确定各线框所表示平面的形状和相互位置后,然后将这些面根据其相对位置进行组装想象,并借助立体概念,综合想象出立体的形状,如图5-41d所示。
4)补画左视图。补画左视图时,应根据各平面的形状和空间位置,依次画出各面的侧面投影,并根据物体的立体形状(见图5-41e),判断线段的可见性。
平面A、B的侧面投影积聚为横向线a″、b″;平面C、D、F为正平面,侧面投影积聚成竖向线c″、d″、f″;面E为铅垂面,侧面投影为类似形线框e″;平面G为水平面,其侧面投影积聚成水平线g″。最后判断出面A、B、G的可见性,求得左视图,如图5-41f所示。
2.形体切割法
形体切割法就是识图时,根据已知视图中外形线框的特点,想象出其立体形状,并以此形体为基础,结合视图中的线段和线框所表示的平面和空间位置,对基本体进行切割,形成物体的形状。
形体切割法的关键是确定剖切面的位置,想象截交线、截交面的形状,从而想象出整体的形状。
例5-19 如图5-42a所示,已知撞块的三视图,想象物体的形状。
1)确定切割基本体的形状。通过对已知视图的分析可知,视图中外形线框均是矩形缺口或缺角,初步确定该基本体形状为长方体。
2)确定切割面的位置。切割平面通常都是特殊位置平面,三个视图中均有反映切割平面积聚性线段。
主视图中线段1′,表示用正垂面Ⅰ切掉长方体的左上角;俯视图中的斜线段2、3,分别表示用铅垂面Ⅱ、Ⅲ在长方体的左边的前、后位置分别斜切掉两个角;左视图中的“凹”形,表示用两个正平面P和一个水平面Q组合切出矩形凹槽。(https://www.xing528.com)
3)想象截断面的形状。当切割平面的空间位置确定后,还需要进一步地想象切割平面在形体上形成截断面的形状。构思时,一般从积聚性线段的视图出发,在相邻视图中找到与其对应的类似形线框或全等形线框,并根据线框的形状想象出截断面的形状。
主视图中斜线段1′分别对应俯、左视图中十边形线框1、1″,想象面Ⅰ为十边形正垂面,如图5-42b所示。
俯视图中斜线段2、3分别对应主、左视图中梯形线框2′、3′与2″、3″,想象面Ⅱ、面Ⅲ为梯形的铅垂面,如图5-42c所示。
左视图中“凹”形线,对应主视图中梯形线框(q′)和俯视图中矩形线框p,想象凹槽底面为矩形水平面P,凹槽侧面为梯形正平面Q,如图5-42d所示。
4)综合起来想象整体。搞清楚各截断面的形状和空间位置后,还需要根据基本体的形状、截断面的形状和基本体的相对位置进行切割想象,综合想象出物体的形状,如图5-42e所示。
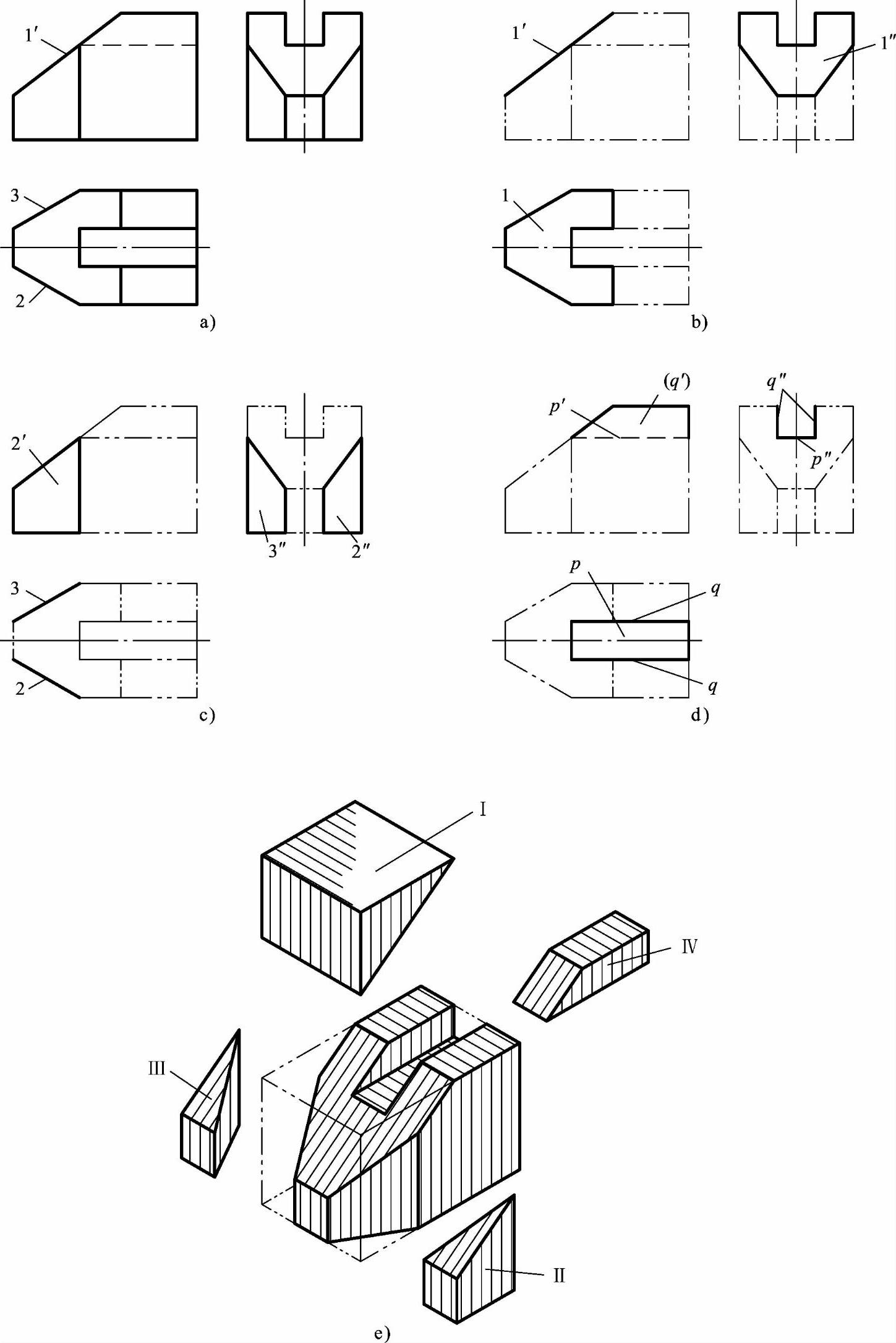
图5-42 形体切割法
要注意的是,形体切割法的识图思路不是唯一的。如在上例中,设想物体是由一个长方体被面A、B、C、P、Q切割而成的;也可以设想该物体是五棱柱被面B、C、P、Q切割而成的;还可以设想该物体是一个六棱柱体被面A、P、Q切割而成的。显然,上述三种思路都可以,但构思时,基本体被切割的次数越少,需要分析的线、面也越少。
例5-20 如图5-43a所示,已知主、俯视图,求作左视图。
1)看图想象立体形状。通过对已知视图的分析可知,俯视图中两个内、外矩形线框对应主视图中的矩形线框,想象基本体的形状为带矩形孔的四棱柱体;主视图中三角形线框对应俯视图中两条虚线段,想象为在四棱柱体上由前向后挖切一个三角形通孔。
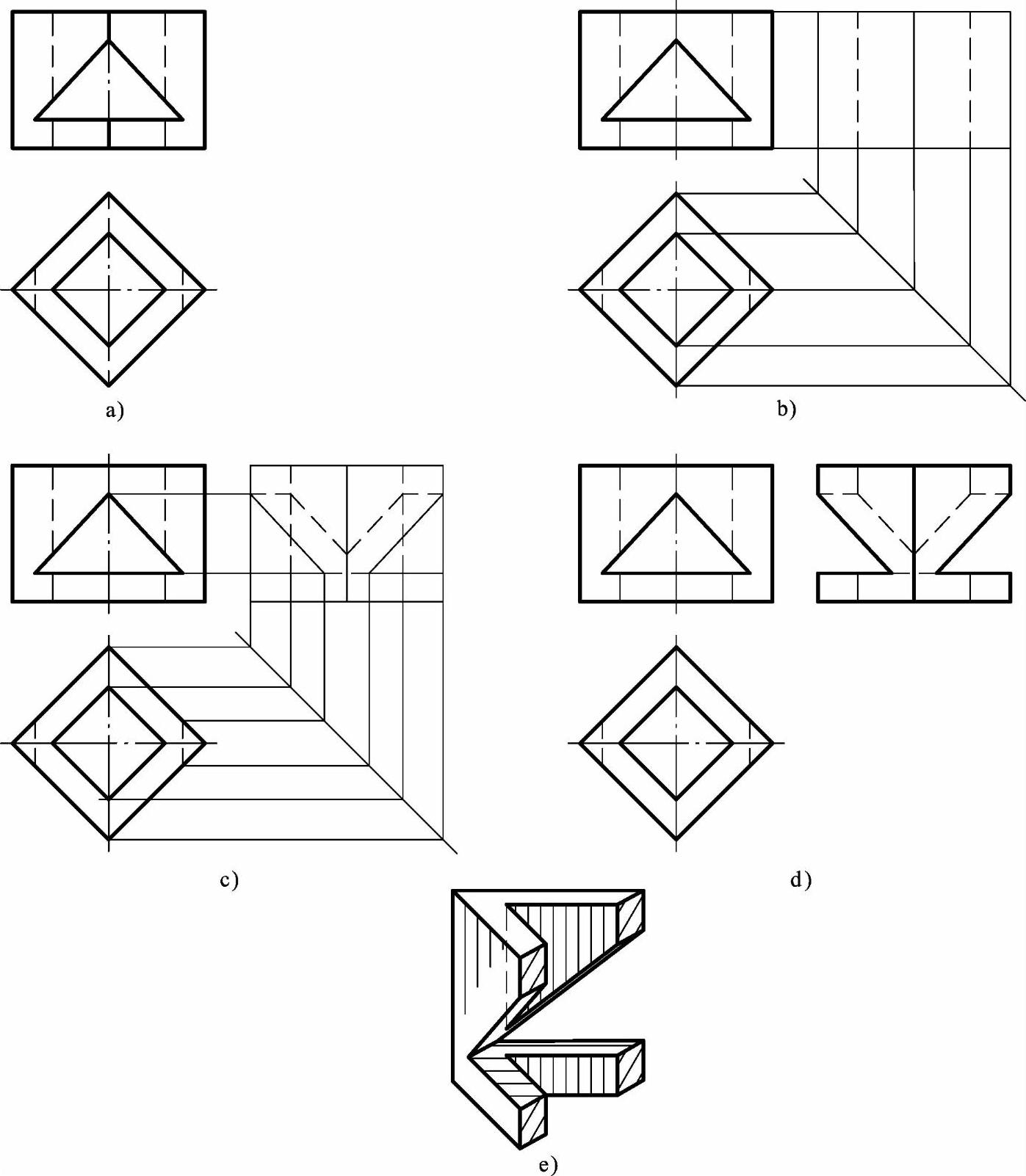
图5-43 已知主、俯视图,求作左视图
在物体的形状确定后,还需确定三角形孔壁的形状。由主视图中斜线对应俯视图中线框,想象四棱柱体被两个相交的正垂面切割,在四棱柱体孔内形成左右对称的七边形截断面。由主视图中水平线段对应俯视图中线段,想象为三角形的水平底面。水平底面与四棱柱面和内矩形孔面相交,形成外六边形内四边形的截断面。最后综合想象出物体的形状,如图5-43e所示。
2)补画左视图。通常求作此类视图时,根据已知视图,利用“三等”投影关系,先画出完整的基本体的投影,再画出相交线或截交线的投影。
画基本体的侧面投影。注意矩形孔应用虚线画出,如图5-43b所示。
画三角形孔的侧面投影。三角形孔的左、右侧面是七边形的正垂面,其侧面投影为七边形;三角形孔的底面是水平面,其侧面投影积聚成水平线段。作图过程如图5-43c所示。
最后判断线段的可见性,擦去被切除部分的投影线,如图5-43d所示。
3.形体凸、凹设想法
当已知视图中,出现两个以上的特征线框在相邻视图中有多条线段对应,而又不能利用“三等”投影关系分清线框的对应位置时,可把这些线框设想为表示凸、凹结构,并通过线框所对应线段的可见性来确定各自的对应关系,最后借助立体概念想象出物体的形状。
例5-21 如图5-44a所示,已知主、俯视图,想象立体形状,补画左视图。
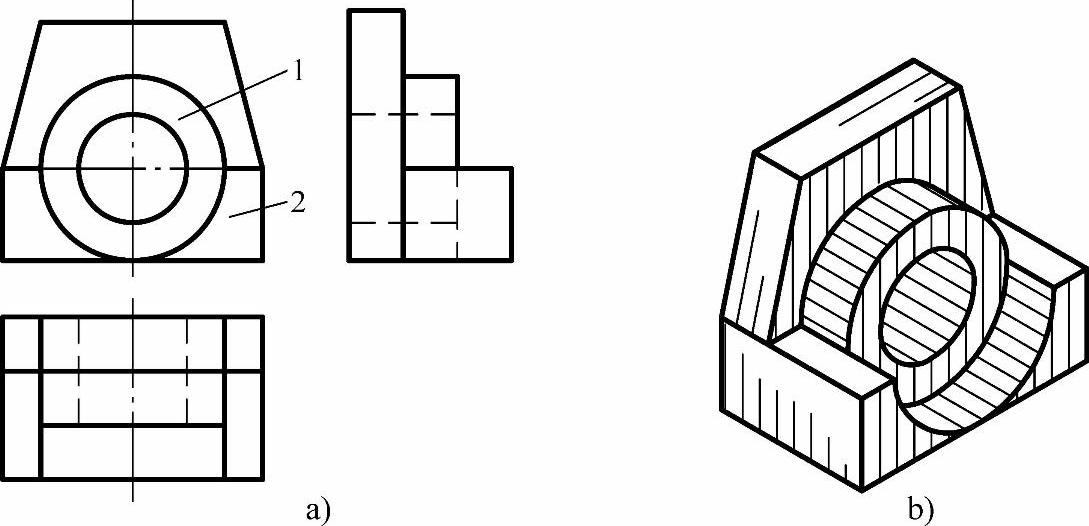
图5-44 凸、凹构型
1)在特征视图中分离出特征形线框。根据已知视图确定特征视图,并在该视图中分离出特征形线框。主视图为特征视图,分离出特征形线框。
2)根据形体凸、凹关系,判断线框与线段的对应位置。主视图中四个特征形线框在俯视图中无类似形线框对应,则对应横向线。线框同长线,不能依靠主、俯视图“长对正”在俯视图中找到各自对应关系,而且同时对应两条实线,分不清各自确切的位置。根据主视图相邻线框对应俯视图为两条实线,一定是上边线框对应出位于后方的实线,下边线框对应出位于前方的实线,形体特点为上凹、下凸。
设想面1在前、面2在后,则形体特点为1凸2凹,这种形体在俯视图中会出现虚线,违反题意。
3)综合起来想象整体。分别想象出各个面的凸凹位置后,还必须从物体应有厚度的立体概念,从俯视图所示的宽度,分清物体各部分的层次,确定各部分的凸、凹和通孔关系,综合想象出带圆柱孔的有三层凸凹结构的柱状类物体(见图5-44b)。
4)求作左视图。如图5-44a所示。
主视图不变,改变一下俯视图,还可以变成图5-45所示的情况。
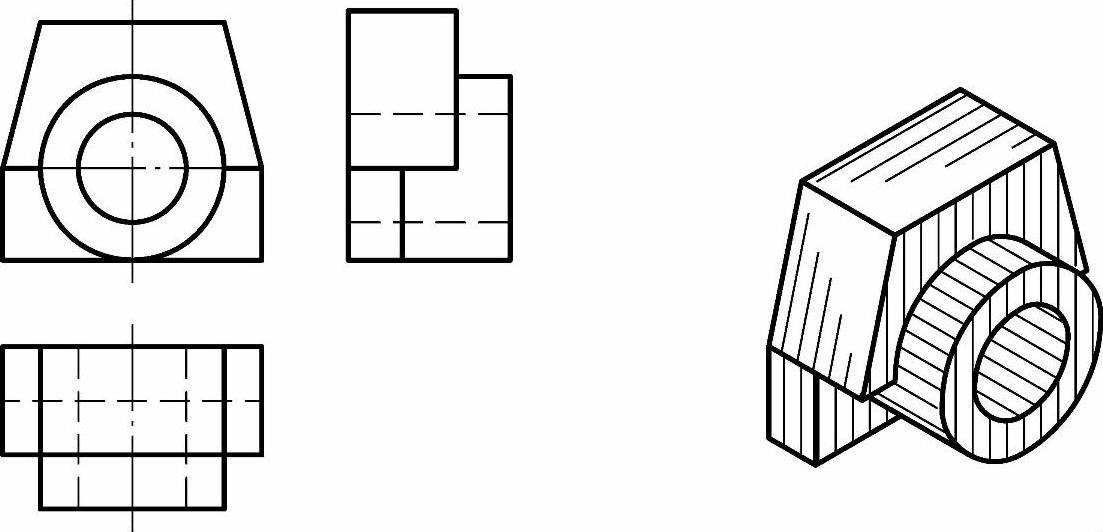
图5-45 凸、凹构型
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




