投影规律和识图方法解析

如图2-1a所示，三棱锥在三投影面体系中，顶点S到其侧面投影（s″）的距离来确定X（长）方向的坐标值；顶点S到其正面投影（s′）的距离来确定Y（宽）方向的坐标值；顶点S到其水平面投影（s）的距离来确定Z（高）方向的坐标值。这样，X值表示空间点S到侧面的距离，Y值表示空间点S到正面的距离，Z值表示空间点S到水平面的距离，书写形式为S（X，Y，Z）。如S（50，30，20），即空间点S距离侧面为50mm，距离正面为30mm，距离水平面为20mm。有了这三个坐标值，就能确定点的空间位置。

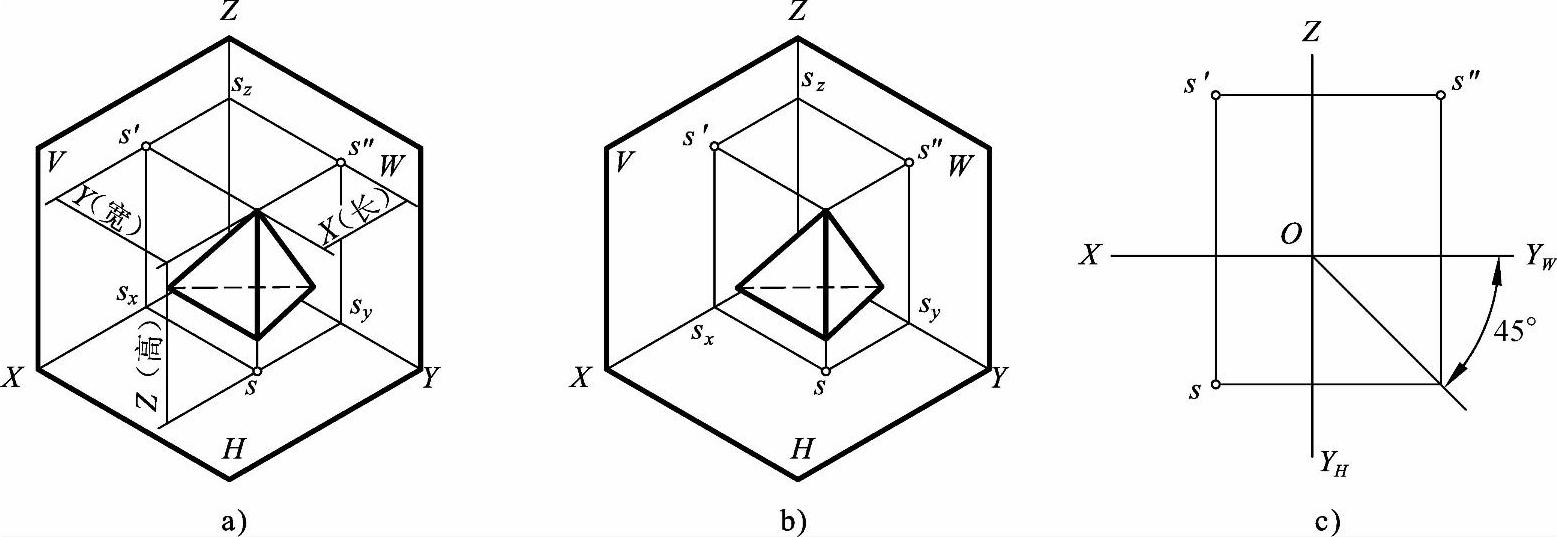
图2-1 点的投影与坐标关系

如图2-1b所示，由点S分别向三个投影面引垂线，其垂足是s′、s、s″，即为空间点S分别在正面、水平面和侧面上的投影，与三视图形成的方法一样展开，最后就形成点的三面投影，如图2-1c所示。点的三面投影具有下述投影规律。

1）点的两面投影的连线必垂直于投影轴，即：

s′s⊥OX

s′s″⊥OZ

ss_YH⊥OY_H、s″s_YW⊥OY_W

2）点的投影到投影轴的距离，等于空间点到对应投影面的距离，即：

s′s_x=s″s_Y=点S到H面的距离Ss(www.xing528.com)

ss_x=s″s_z=点S到V面的距离Ss′

ss_Y=s′s_z=点S到W面的距离Ss″

根据上述投影规律，已知点的三个坐标值，就能作出该点的三面投影。反之，知道点的两面投影，也就等于已知该点的三个坐标。同时，在点的三面投影中，知道点的任意两个面的投影，就可以求作出第三个投影。如图2-2所示，箭头所指得到的投影就是需要求作的第三个投影。

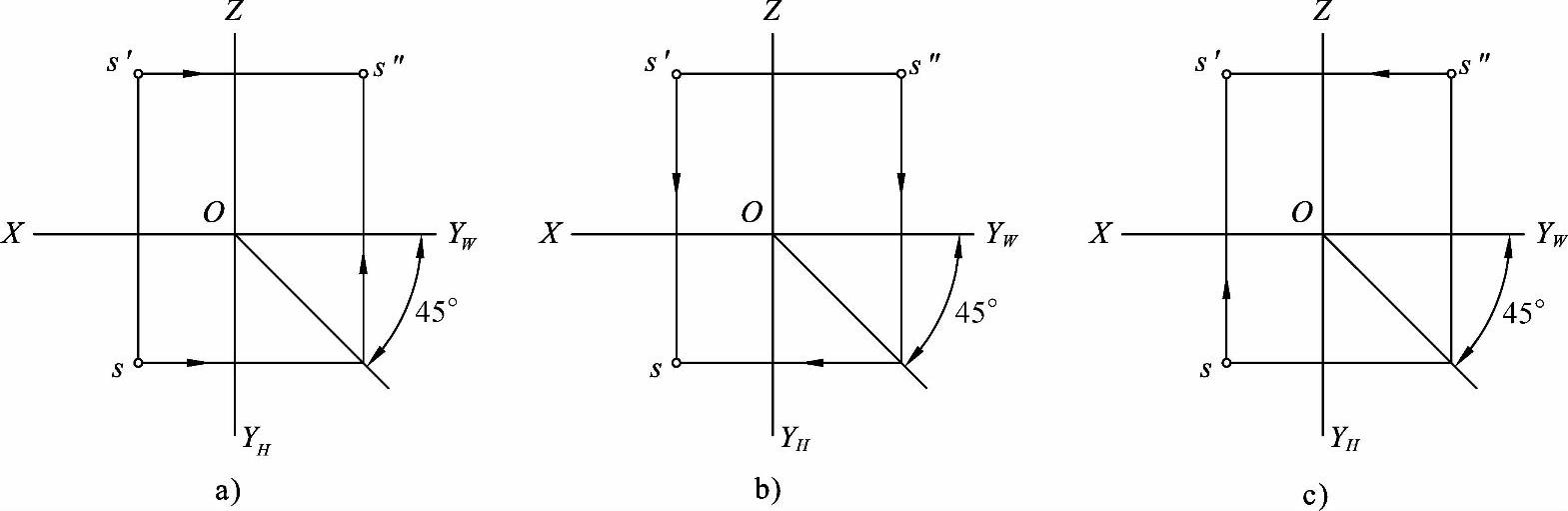
图2-2 已知两个投影求作第三个投影

如图2-2a所示，已知点的正面投影、水平投影，可以作出侧面投影。

如图2-2b所示，已知点的正面投影、侧面投影，可以作出水平面投影。

如图2-2c所示，已知点的水平投影、侧面投影，可以作出正面投影。