1)_movePathLinear:可实现在2D或3D平面中的直线路径插补运动。
MCC编程示例如图9-19所示。
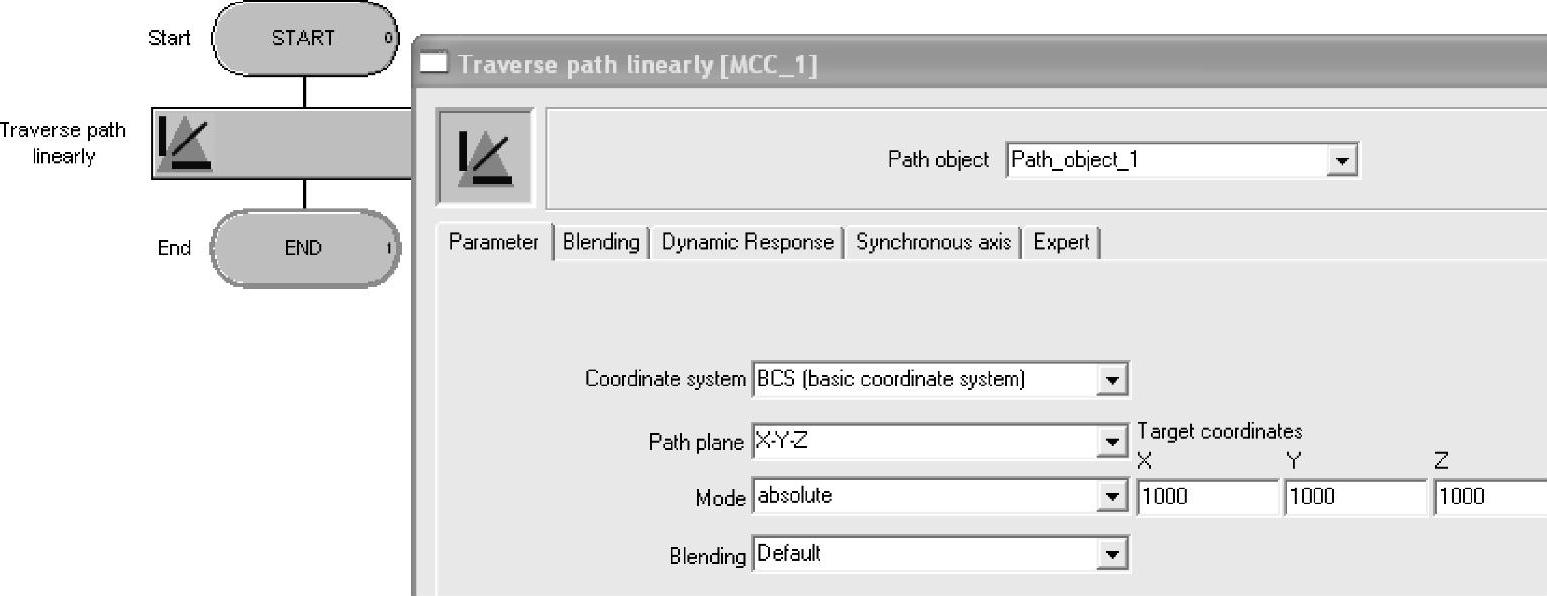
图9-19 直线路径插补MCC编程
ST编程示例如图9-20所示。

图9-20 ST编程示例
2)_movePathCircular:可实现下述方式的圆弧路径插补运动。
①在2D主平面中通过指定半径,结束点及方向的圆弧路径;
②在2D主平面中通过指定圆心及角度的圆弧路径;
③在2D主平面中通过指定中间点及结束点的圆弧路径;
④在3D主平面中通过指定中间点及结束点的圆弧路径。
MCC编程示例如图9-21所示。
ST编程示例如图9-22所示。
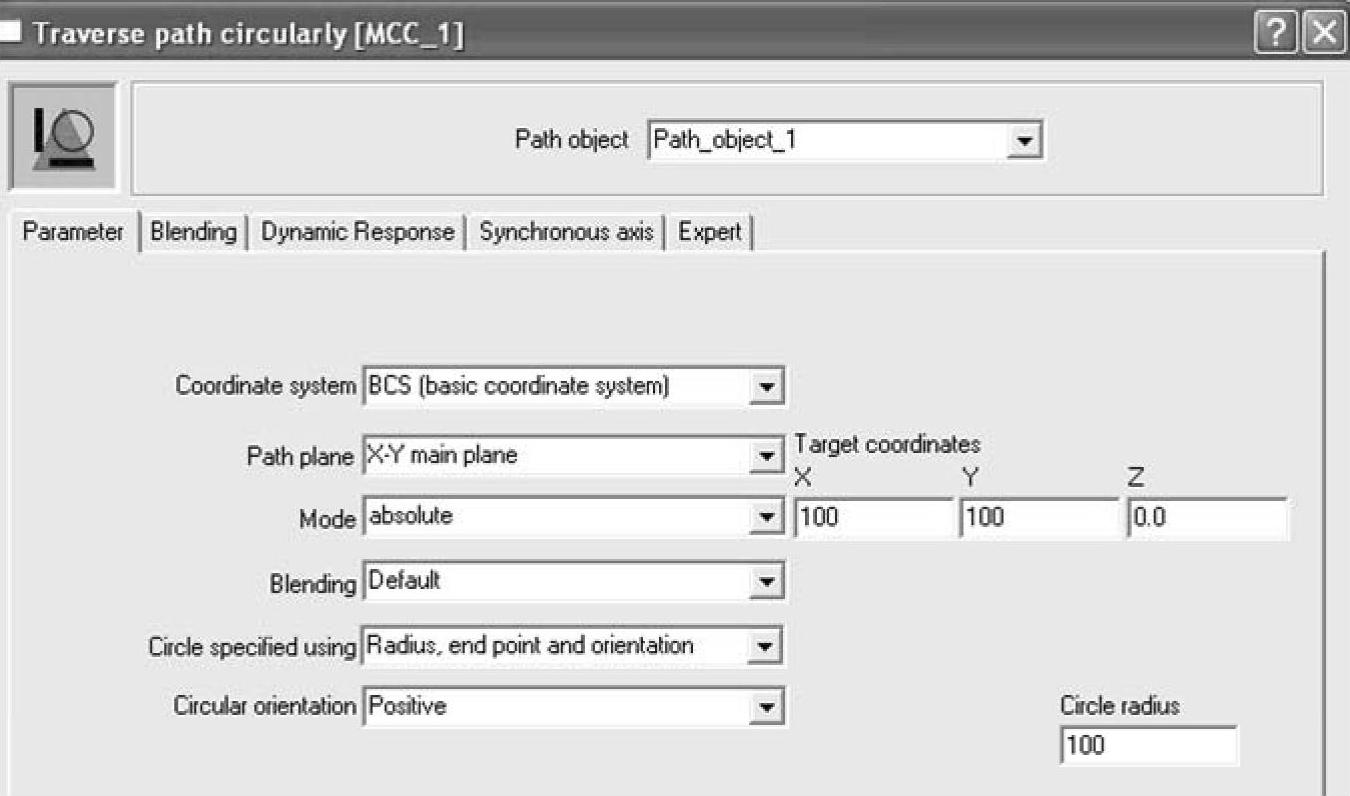
图9-21 圆弧路径插补MCC编程

图9-22 ST编程示例
3)_movePathPolynomial:可实现多项式路径插补运动。
在高级路径插补应用中,如圆弧路径插补不能满足设计需求,则可借助多项式路径插补来完成。需要注意的是,路径插补中用到的多项式变量均为矢量。有下述三种多项式路径插补的定义方法:
①根据五阶多项式的系数来完成插补,在编程时需要提供的数据包括目标位置以及四个空间矢量坐标。MCC编程示例如图9-23所示。
ST编程示例如图9-24所示。
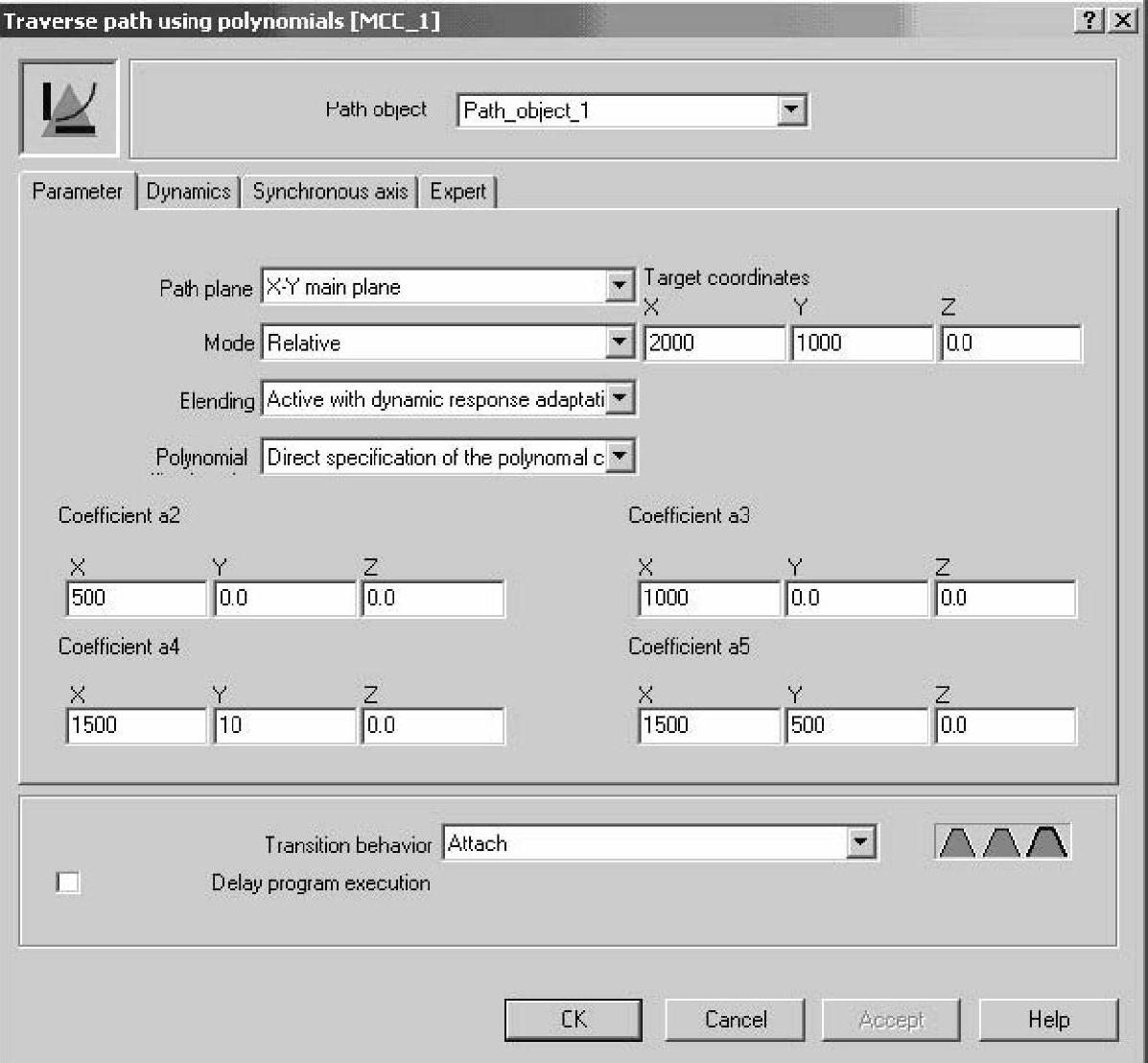
图9-23 多项式路径插补MCC编程

图9-24 ST编程示例(https://www.xing528.com)
②根据起始位置与目标位置的几何微分完成多项式插补,在编程时需要提供这些数据。下面以一个连接一条直线与一段圆弧的多项式曲线为例来说明多项式路径插补运动的具体编程方法,如图9-25所示。
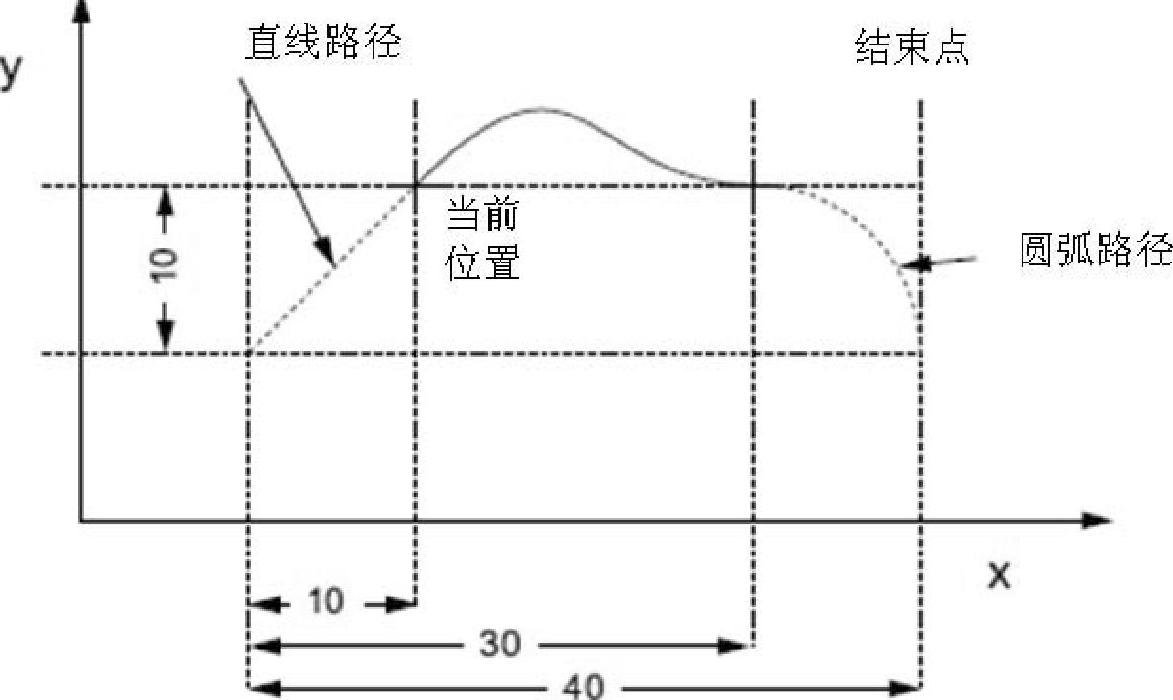
图9-25 多项式插补示例
步骤1 使用_getLinearPathGeometricData功能块,通过直线结束点(多项式的开始点)计算出连接多项式插补路径开始点的两个微分。
步骤2 使用_getCircularPathGeometricData功能块,通过圆弧路径的开始点计算出连接多项式插补路径结束点的两个微分。
ST编程如图9-26所示。

图9-26 ST编程
步骤3 使用_movePathPolynomial命令运行连接直线段与圆弧段中间的多项式路径。ST编程如图9-27所示。

图9-27 ST编程
4)_stopPath():用于停止当前的路径插补运动。
MCC编程如图9-28所示。
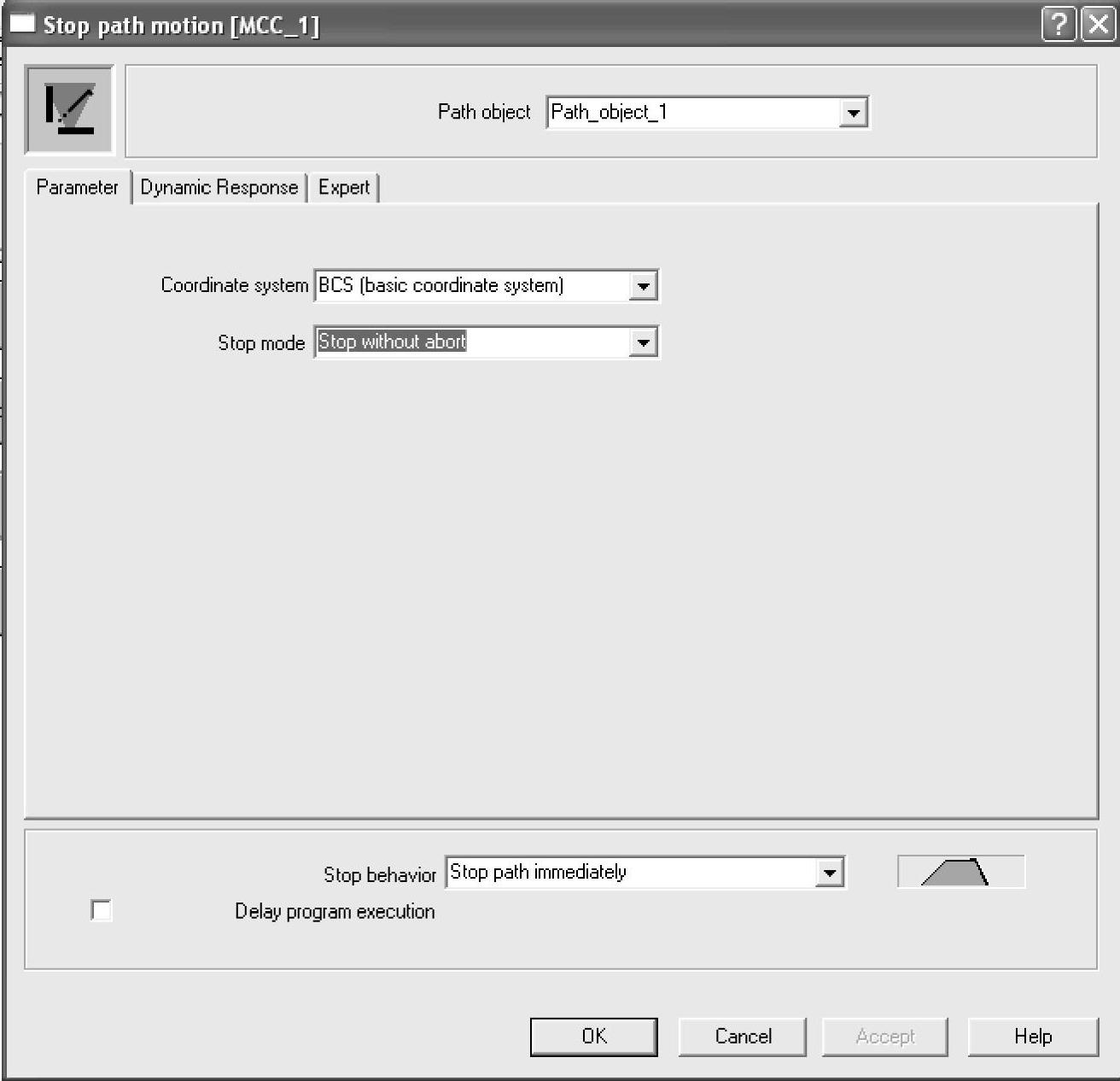
图9-28 MCC编程
ST编程如图9-29所示。

图9-29 ST编程
5)_continuePath:用于继续运行停止的路径插补运动。
MCC编程如图9-30所示。
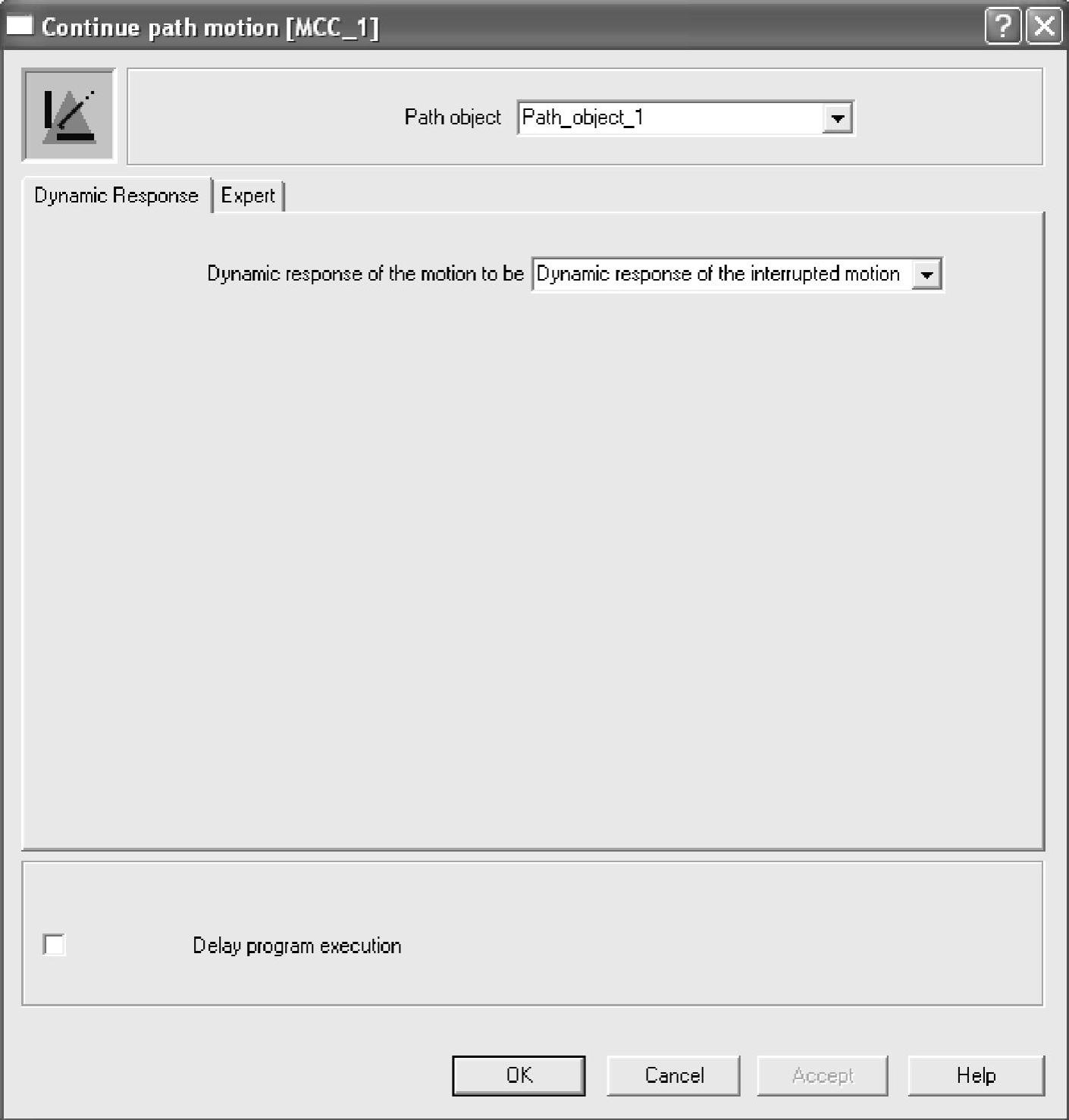
图9-30 MCC编程
ST编程如图9-31所示。

图9-31 ST编程
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




