理论计算与试验结果的对比分析

利用上述模型对实际熔断器进行理论计算，对比试验结果评估计算结果的准确性，同时研究各种热流模型成立的条件。

上述模型的一个核心内容是确定熔体内的电流分布。下面举一个具体例子，假定不同熔体的材料和电阻率一样，具体数值是银在20℃的电阻率值，在这种条件下，对多个熔体进行计算。显而易见，知道熔体的电流分布就可以轻而易举地得到熔体的电阻。利用同样的方法对多个熔体进行计算，如果结果一致，计算方法就可以得到验证。

在后续的计算中发现，在电弧发生前的不同阶段，随着熔体不断变热引起输入能量变多，熔体温度不断接近熔点，熔体狭颈的电阻率随之升高，熔体的整个电阻也明显变大，但是电流分布方式变化不明显，如图2-11中，实线表示最初的冷态（弧前阶段起始的时间）的电流分布，虚线表示狭颈接近熔体熔化温度（弧前阶段结束的时间）时的电流分布曲线，可以看出，弧前阶段开始和结束时电流分布变化甚微。

在电流很大（即接近或达到短路条件）的情况下，假定熔体不发生热传导，利用前述方法计算各种熔体形状的弧前时间，发现对于圆柱状的熔体，弧前时间接近35 ms，理论计算数值和试验结果高度吻合。对于很多满足IEC60269-2-1的现代工业熔断器，只有弧前时间在3 ms或更小时，计算结果和试验结果才比较吻合。对于半导体熔断器，限制条件就更加严格，只有弧前时间在0.3 ms或更小时，计算结果与试验结果才比较接近。由此得出一个有趣的结论：尽管这个方法简单，但是当熔体的热传导可以忽略时，熔断器时间-电流特性的理论计算结果在较大的范围内是准确的。对于现代熔断器，这种方法的适用范围是严重发生短路的情况。

在电流比较大的情况下，假定只在熔体内部发生热传导，熔体与周围介质不发生热传导，发现工业熔断器的弧前时间在5 ms、半导体熔断器的弧前时间在10 ms左右时，计算结果和试验结果非常吻合。

图2-11　熔体在均匀及非均匀温度分布情况下的电流曲线

其中：
实线表示均匀温度分布情况下的电流曲线，
虚线表示非均匀温度分布情况下的电流曲线。

当电流更小时，假定在熔体内部以及熔体与周围介质间都发生热传导，对一种半导体熔断器的计算结果连同试验结果绘制在图2-12中，可以看到，当弧前时间达到5～10 s时，计算结果与试验结果开始偏离，意味着在这个时间量级，熔断器热传导范围加大，散热效果明显。

在理论计算中发现一个有趣的现象：对于i＝Ipksinωt的正弦波交流电，时间-电流曲线出现不连续断裂，这个现象在试验中也被发现，原因当时不被理解。在电流值变大时熔体迅速升温，如果在电流达到峰值前熔体不发生汽化，在随后的四分之一周期电流值降低、输入熔体的能量减少，热量自熔体扩散，熔体温度降低，这种现象对于带有狭颈的非均匀熔体尤为明显。由于热传导，熔体在电流经过峰值后的瞬间达到最高温度。对于进行计算的具体熔断器，在电流（i＝Ipksinωt）降到零点后的6～7 ms熔体达到最高温度，熔断器只有在这个时间段断开，否则要等到电流再次升高时才会动作，这种现象在过载电流水平（过载电流的一般定义是额定电流的1～10倍）阶段发生，如图2-13所示，图中描绘了在两种故障电流情况下熔体狭颈温度随时间的变化：第一种情况是故障电流的RMS（均方根）等于1550 A，熔断器在第一个半周期（6.5 ms）断开；第二种情况在第二个半周期内（15 ms）断开。这个结果在试验中得到验证，熔断器按照计算结果进行设计，加载故障电流后在7～14 ms断开。很明显，熔断器在40 ms内的动作特性由电流波形决定。对于正弦波电流，其行为一方面受故障发生时电压相位影响；另一方面，电路参数会影响电流的瞬态分量，进而也影响熔断器的动作特性。(www.xing528.com)

图2-12　200 A半导体熔断器的弧前时间-电流曲线（50 Hz正弦波交流电）

其中：
（1）实线代表计算预测结果；
（2）圆圈代表实验结果；
（3）虚线代表绝热（即不发生热传导）条件下的计算结果；
（4）实线与虚线偏离的原因见上面的分析。

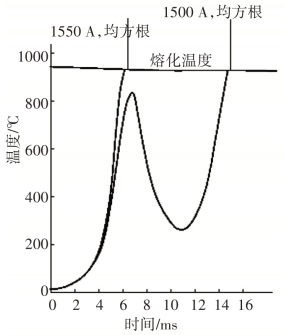
图2-13　半导体熔断器熔体狭颈温度与正弦波RMS电流值的关系

对于更小的故障电流，熔断器反应时间会变得很长，这个时候，只有电流的RMS（均方根）值对熔断特性产生有效控制，瞬态变量的影响在理论分析中可以忽略。

利用本章介绍的方程式很容易获得熔断器温度分布的信息，这种信息用其他方法很难得到，而这些信息无论是对熔断器设计人员还是对熔断器应用人员都非常有用。对一种额定电流为200 A的半导体熔断器承载900 A和1200 A两种情况分别进行理论计算，900 A的情况下，在弧前时间约等于0.7 ms时熔体狭颈达到熔化温度，狭颈的温度约为916℃，1200 A的情况下狭颈的温度约为880℃。一个很有趣的结论是：流经熔断器的故障电流越大，熔体大部分地方的温度越低！原因是：故障电流越大，弧前时间越短，从狭颈扩散到熔体其他部位的热量越少。

利用前面介绍的方法计算不同熔断器的最小熔断电流，理论计算值与试验结果非常一致。在额定电流下，连接电缆的横截面积对熔断器的温度分布有明显的影响。

“有限差分法”可以用来对热电阻电容网络建模，这样就可以应用标准的电路分析软件获得熔断器的温度分布。不过绝大部分熔断器都含有多条带狭颈的平行熔体，在实际的设计过程中必须考虑三维模型，建立一个数量庞大而又颇为复杂的小区块网阵，在狭颈处小区块体积很小，在靠近管壳及连接端子的区域小区块体积比较大。为了使运算成本在可接受范围，必须做出恰当的简化。有人利用有限差分法仿真一个实际的半导体熔断器，计算结果相当精准，只是运算时间很长。随着计算机运算能力的提高，有限差分法会逐步成为熔断器设计的一个常规工具。