接近最小熔断电流水平的弧前特性优化方案

当熔断器的弧前时间变得更长的时候，虽然也可利用上一节介绍的方法进行计算，但是热传导的情况要复杂很多，计算时间长得令人无法接受，因此有必要寻找不同的方法进行计算。

前面介绍到，对于每一种熔断器，存在一个电流值，当等于这个值的电流通过熔断器的时候，熔体熔化所需要的时间在理论上是无限长，电流-时间曲线是接近此电流值的一条渐近线，这个电流值大致接近熔断器的最小熔断电流水平。在这种情况下，熔体的温度和电阻率的变化极其缓慢，可以认为熔体达到稳定状态，熔体内存储的能量不再发生变化。对这种平衡状态的条件进行分析，可以获得熔体狭颈达到熔点时的电流值。

按照这种方法进行计算时，不仅要考虑在熔体内部发生热传导，同时还要考虑熔体与周围填充介质之间以及与连接端子之间发生热传导，这个时候要把熔断器的不同部件及材料分解为多个小区块，对每个小区块按照三维模型进行计算。每个小区块要保持在能量平衡状态，任何一个时间段内该小区块自身产生的热能与从外部流入的热能之和必须等于同一时间段内散失掉的热能，也就是说，它存储的能量要保持不变。要考虑到具有不同热导率的两种材料之间发生热传导。如图2-9a所示，（m，n）和（m+1，n）是两个相邻的小区块，假定每个小区块从它的中心到边界的温度梯度恒定，如图2-9b所示：

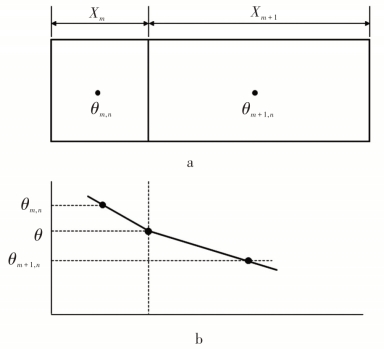
图2-9　不同材料的小区块之间的热传递

其中，Km，n为小区块（m，n）的热导率；Km＋1，n为小区块（m＝1，n）的热导率；Z为厚度。

那么这两个小区块之间传递的热量可以表达为：

（1）在Δt时间内从（m，n）流入（m+1，n）的热传递是：

其中θ是边界的温度。

（2）同时，在Δt时间内从（m，n）流入（m＋1，n）的热传递是：

上面两个公式相等，θ可以去掉，得到下面的公式：

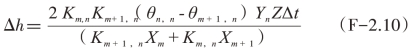(www.xing528.com)

当热量通过一个较短路径的具有高热导率的小区块，流入一个较长路径的具有低热导率的小区块时，由于Km+1，n＞＞Km，n及Xm＞＞Xm+1，方程式（F-2.10）可以简化为：

方程式（F-2.11）可以应用在熔断器管体与管帽之间或者熔体与填充介质之间的热传导分析，这样可以大大减少计算量。

在图2-10中，任何一个小区块的周围有6个小区块向它传递热量，即：向小区块（m，n，p）传入的总热量为：

在任何时间段内，传入小区块（m，n，p）的热量（Δhc）和它产生的热量（Δhg）之和等于它由于对流及辐射散失的热量（Δhl），即：

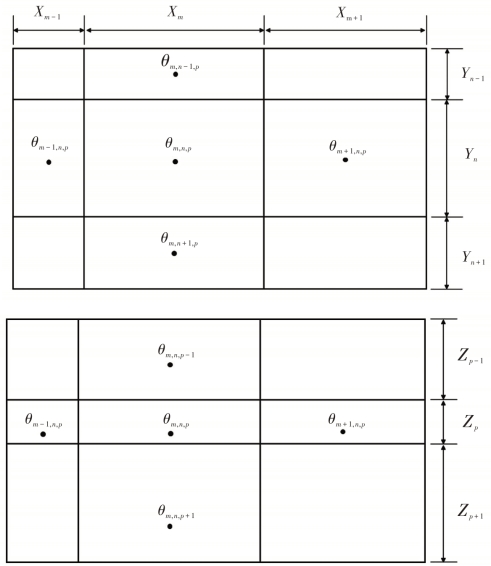
图2-10　7个相邻小区块

其中，Km，n，p、Km，n，p＋1分别是小区块（m，n，p）和（m，n，p+1）的热导率。

由方程式（F-2.12）和（F-2.13）导出小区块（m，n，p）的温度θm，n，p如下：

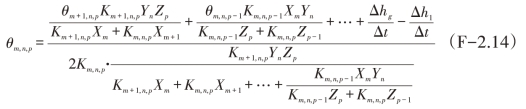
在（F-2.14）中，只有流过电流的小区块的Δhg不为零，其他小区块的Δhg都为零，同样地，只有熔体表面小区块的Δhl不为零，其他小区块的Δhl都为零，在这种情况下，电阻率的一个或多个因子都为零。

对于某一个特定的电流值，利用迭代过程可以获得稳态温度分布，进而可以得到电阻率及电流分布。重复这个计算过程可以得到熔体狭颈达到熔点的电流值。利用同样的方法，也可以确定熔断器承载电流小于最小熔断电流情况下的稳态条件。