大电流情况下的弧前特性分析

当熔断器承载的电流比上一节讨论的电流值稍微小的时候，弧前时间会变得更长一些，此时需要考虑热传递。对于含有狭颈熔体的熔断器，当流经熔断器的电流大到一定范围时，弧前时间依然较短；考虑到熔体周围介质及部件的热导率比较低，可以假定热传递仅仅局限在熔体内部，熔体与周围介质及部件不发生热传递。当这种假设成立时，计算弧前时间既要考虑热传导也要考虑热存储过程，而这些过程受熔体几何形状和尺寸的影响。很明显，热量要从狭颈处扩散到电流密度较小的地方，这样狭颈熔化和汽化所需要的时间势必会变长。在实际应用中，这一点在一定程度上可以用来控制和设计熔断器的特性，例如：如果将紧挨着狭颈的熔体尺寸变大，此处的电流密度、能量密度变小，温度变低，从狭颈处吸收的热量变多，从而使狭颈熔化和汽化所需要的时间变长。

上述过程定性理解很容易，定量分析熔体几何形状的影响需要求解相关的能量方程式。下面介绍一种分析含有狭颈熔体的熔断器特性的具体方法：第一步，确定熔断器的电流分布，第二步，将一根熔体分解成数个小区块，如图2-8所示。由于熔体的横截面积不变，假定从如图小区块流失的热损耗可以忽略不计，可以简化成一个二维模型进行分析。

图2-8　5个相邻小区块示意图

很明显，两个相邻的小区块之间的热流传导与两个小区块中心的温度差及热流横截面积成正比，与两个小区块的中心间距成反比。

在图2-8中，在时间Δt内传入小区块（m，n）的热流如公式（F-2.5）所示：

其中：

K为热导率；Z为厚度；θm，n、θm－1，n、θm＋1，n、θm，n-1、θm，n＋1分别是相邻小区块的平均温度，亦即小区块的中心点的温度。假定小区块在热传导发生之前的平均温度是θ′m，n，在Δt内，小区块（m，n）内的热能增加量由公式（2.6）给出：

(www.xing528.com)

其中，D为密度，λ为比热容。很明显，对于任何一个小区块，流入它的热能（ΔhC）与它内部产生的热能（Δhg）之和等于它存储的热能增加量（Δhs）：

利用公式（F-2.5）、（F-2.6）和（F-2.7）可以得出θm，n与周围小区块的平均温度的关系，如公式（F-2.8）所示：

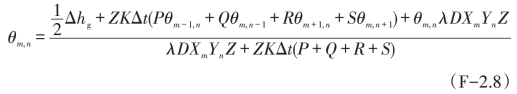
其中：

利用“超松弛迭代法”求解方程式（F-2.8）获得任意一个时段中间点的温度分布。小区块在一个时段的起始点和结束点的温度可以通过公式（F-2.9）获得：

其中：θ是小区块（m，n）在时段中的平均温度；θ′是小区块（m，n）在时段开始时的温度；θ″m，n是小区块（m，n）在时段结束点的温度。

利用小区块的最终温度可以计算得到小区块的电阻率，利用电阻变化可以计算出电流分布，进而获得输入到小区块的能量。利用这种方法不断迭代最终可以计算出狭颈区域小区块发生熔化和汽化的参数。