加减速度控制的应用与优化

在闭环和半闭环CNC系统中，加减速控制多数都采用软件来实现，这样给系统带来了较大的灵活性。这种用软件实现的加减速控制既可以在插补前进行，也可以放在插补后进行。放在插补前的加减速控制称为前加减速控制，放在插补后的加减速控制称为后加减速控制，如图4-23所示。

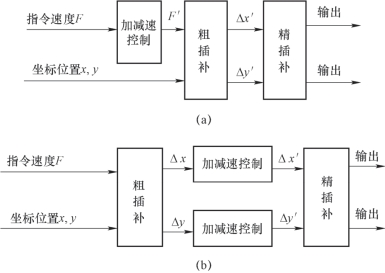
图4-23　加减速控制

（a）前加减速控制；（b）后加减速控制

前加减速控制的优点是仅对合成速度——编程指令速度F进行控制，所以它不会影响实际插补输出的位置精度。前加减速控制的缺点是需要预测减速点，而这个减速点要根据实际刀具位置与程序段终点之间的距离来确定。这种预测工作需要完成的计算量较大。

后加减速控制与前加减速相反，它是对各运动分别进行加减速控制，这种加减速控制不需要专门预测减速点，而是在插补输出为零时开始减速，并通过一定的时间延迟，逐渐靠近程序段终点。后加减速的缺点是，由于它对各运动坐标轴分别进行控制，所以在加减速控制以后，实际的各坐标轴的合成位置就可能不准确。但是这种影响仅在加速或减速过程中才会有，当系统进入匀速状态时，这种影响不存在。

1.前加减速控制

1）稳定速度和瞬时速度

所谓稳定速度是指系统处于稳定进给状态时，在一个插补周期内每插补一次的进给量，实际上就是指令速度F（单位为mm/min）需要转换成每个插补周期T（单位为ms）的进给量。另外，为了调速方便，设置了快速进给倍率开关、切削进给倍率开关，这样在计算稳定速度时，还需要将这些因素考虑在内。

稳定速度的计算公式为

式中　Fs——稳定速度，单位为mm/min；

T——插补周期，单位为ms；

F——指令速度，单位为mm/min；

K——速度系数，包括快速进给倍率、切削进给倍率等。

除此之外，稳定速度计算完后，进行速度限制检查。如果稳定速度超过由参数设定的最大速度，则取限制的最大速度为稳定速度。

所谓瞬时速度，就是系统在每个插补周期的实际进给量。当系统处于稳定进给状态时，瞬时速度Fi等于稳定速度Fs，当系统处于加速状态时，Fi＜Fs；而当系统处于减速状态时，Fi＞Fs。

2）线性加减速控制

当机床启动、停止或在切削加工过程中改变进给速度时，系统自动进行线性加减速控制。加减速速率分为快速进给和切削进给两种，它们必须作为机床参数预先设置好。设进给速度为F（单位为mm/min），加速到F所需的时间为t（单位为ms），则加减速度a为

（1）加速处理。系统每插补一次都要进行稳定速度、瞬时速度和加减速处理。若给定稳定速度要作改变，当计算出的稳定速度大于原来的稳定速度Fs时，则要加速；或者，给定的稳定速度Fs不变，而计算出的瞬时速度Fi＜Fs，则也要加速。每加速一次，瞬时速度为

新的瞬时速度Fi+1参加插补计算，对各坐标轴进行进给增量的分配。这样，一直加速到新的或给定的稳定速度为止。其加速处理程序流程图如图4-24所示。

（2）减速处理。系统每进行一次插补运算后，都要进行终点判断，也就是要计算出离终点的瞬时距离Si，并按本程序段的减速标志，判别是否已到达减速区，若已到达，则要进行减速。如果稳定速度Fs和设定的加减速度a已确定，可用下式计算出减速区域S。

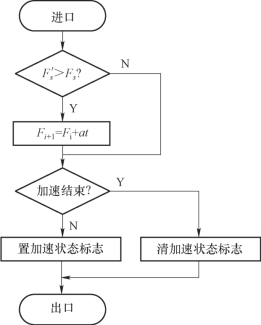
图4-24　加速处理程序流程图

因为

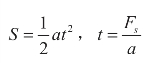
所以

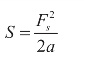
若本程序段要减速，即Si≤S，则设置减速状态标志，并进行减速处理。每减速一次，瞬时速度为

Fi+1=Fi -at

新的瞬时速度Fi+1参加插补运算，对各坐标轴进行进给增量的分配，一直减速到新的稳定速度或减到零。如要提前一段距离开始减速，则可按需要，把提前量ΔS作为参数预先设置好，这样，减速区域S的计算式为

其减速处理程序流程图如图4-25所示。

（3）终点判别处理。在前加减速处理中，每次插补运算后，系统都要按求出的各轴插补进给量来计算刀具中心离开本程序段终点的距离Si，并以此进行终点判别和检查本程序段是否已到达减速区并开始减速。

①直线插补时Si的计算。如图4-26所示，直线的起点在原点O，终点坐标为P(xa,ya )，其加工瞬时点A(xi,yi)，插补计算时求得X、Y轴的插补进给增量Δx、Δy后，即可得到A点的瞬时坐标值为

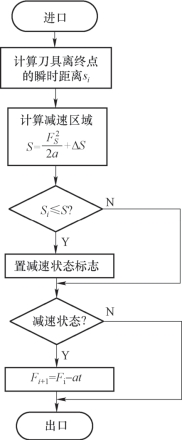
图4-25　减速处理程序流程图

(www.xing528.com)

图4-26　直线插补终点判别

设x轴为长轴，该轴与直线的夹角为α，则瞬时加工点A离终点P(xa,ya)的距离Si为

②圆弧插补时Si的计算。应按圆弧所对应的圆心角小于及大于π两种情况分别进行处理，如图4-27所示。

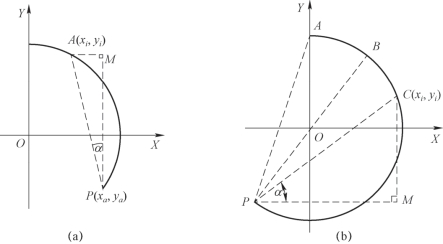
图4-27　圆弧插补终点判别

（a）圆心角小于π；（b）圆心角大于π

如图4-27（a）所示，圆心角小于π时P为圆弧终点，A为顺圆插补过程中的某一瞬时点，则A点离终点的距离为

如图4-27（b）所示，圆心角大于π时圆弧AP的起点为A，终点为P，B点为临界点，从B点到圆弧终点的圆弧段对应的圆心角等于π。C点为顺圆插补过程中的某一瞬时点。显然，瞬时点离圆弧终点的距离Si的变化规律是：当瞬时加工点由A到B点时，Si越来越大，直到它等于直径；当瞬时加工点越过临界点B后，Si越来越小。在这种情况下的终点判别，首先应判别的Si变化趋势，即若Si变大，则不进行终点判别处理，直到越过临界点；若Si变小再进行终点判别处理。

2.后加减速控制

放在插补后各坐标轴的加减速控制称后加减速控制。后加减速控制的规律实际上与前加减速控制一样，通常有直线加减速控制和指数加减速控制。

1）直线加减速控制

直线加减速控制使机床起动时，速度按一定斜率的直线上升，而要停止时，速度沿一定斜率的直线下降，如图4-28所示。这与前加减速控制的线性加减速控制规律完全相同。

2）指数加减速控制

进行指数加减速控制的目的是将启动或停止时的速度突变，变成随时间按指数规律上升或下降，如图4-29所示。指数加减速度与时间的关系可用下式表示：

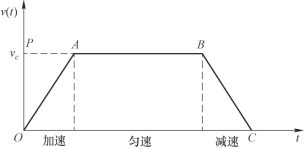
图4-28　直线加减速控制

图4-29　指数加减速

匀速时

v(t)=vc

加速时

减速时

式中　T——时间常数；

vc——稳定速度；

v(t)——被控的输出速度。

图4-30所示为指数加减速控制算法的原理图。图中Δt表示采样周期，其作用是每个采样周期进行一次加减速运算，对输出速度进行控制。误差寄存器E将每个采样周期的输入速度vc与输出速度v之差（vc-v）进行累加，累加结果一方面保存在误差寄存器中，另一方面与1/T相乘，乘积作为当前采样周期加减速控制的输出v。同时v又反馈到输入端，准备下一个采样周期，重复以上过程。

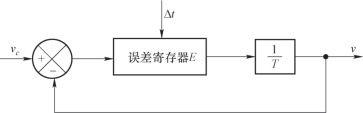
图4-30　指数加减速控制的原理图

上述过程可以用迭代公式来描述，即

式中　ei，vi——第i个采样周期误差寄存器E中的值和输出速度值，且其迭代初值v0、e0为零。

经过数学推导和处理，实用的数字增量式指数加减速迭代公式为

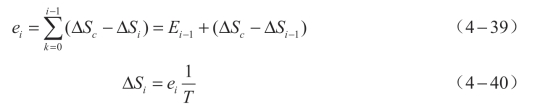
式中　ΔSc——每个采样周期加减速的输入位置增量值，即每个插补周期粗插补运算输出的坐标位置数字增量值；

ΔSi——第i个插补周期加减速输出的位置增量值。

由前述的前加减速控制和后加减速控制的原理可知，前加减速控制的优点是不会影响实际插补输出的位置精度，但需要进行预测减速点的计算，花费CPU的时间；后加减速控制的优点则是无须预测减速点，简化了计算，但在加减速过程中会产生实际的位置误差。