圆弧插补及偏差函数计算方法

1.偏差函数

如图4-7所示，是要插补的圆弧，圆弧的圆心在坐标原点，半径为R，起点为A（xa，ya），终点为B（xb，yb）。点P（x，y）表示某时刻刀具的位置。

图4-7　圆弧插补

圆弧插补时，偏差函数定义为

表示O、P两点的距离，其表达式为

将上式代入式（4-10），得到偏差函数的计算公式

若刀具在圆外，则大于R，偏差函数大于零；若刀具在圆上，则等于R，偏差函数等于零；若刀具在圆内，则小于R，偏差函数小于零。表4-4所示为圆弧插补中偏差函数与刀具位置的关系。

表4-4　圆弧插补中偏差函数与刀具位置的关系

2.进给方向与偏差计算

圆弧可分为顺圆与逆圆两种。与时钟指针走向一致的圆弧称为顺圆，反之称为逆圆。加工这两种圆弧时，刀具的走向不同，偏差计算的过程也不同。下面分别介绍这两种圆弧的插补。

（1）顺圆插补。开始插补时，刀具位于圆弧的起点A，由式（4-11）计算偏差值为

因A是圆弧上一点，由表4-4可知

设某时刻刀具运动到点P1（xi，yi），由式（4-11）知，这时的偏差值为

若Fi≥0，由表4-4可知，这时刀具位于圆外或圆上，如图4-8（a）所示。为让刀具向终点B进给并靠近圆弧，应让刀具沿y轴负向走一步，到达点P2（xi+1，yi+1）。点P2的坐标由下式计算，即

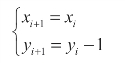
刀具在点P2的偏差值为

把式（4-13）代入上式，简化为

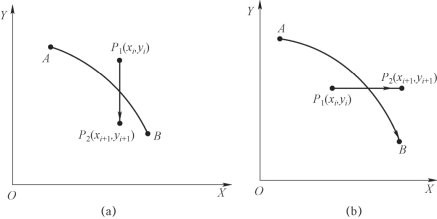
图4-8　顺圆插补的进给方向

若Fi＜0，由表4-4可知，这时刀具位于圆内，如图4-8（b）所示。为让刀具向终点B进给并靠近圆弧，应让刀具沿x轴正向走一步，到达点P2（xi+1，yi+1）。点P2的坐标由下式计算，即

刀具在点P2的偏差值为

把式（4-13）代入上式，简化为

式（4-12）、式（4-14）和式（4-15）组成了顺圆插补偏差值的递推计算公式。与偏差函数的直接计算式（4-11）相比，递推计算公式只用加减法（乘2可用两次加来实现），不用乘法或乘方，计算简单，运算速度快。

顺圆插补的计算过程如表4-5所示。

表4-5　顺圆插补的计算过程

（2）逆圆插补。设某时刻刀具运动到点P1（xi，yi），这时的偏差函数为

若Fi≥0，这时刀具位于圆外或圆上，如图4-9（a）所示。为让刀具向终点B进给并靠近圆弧，应让刀具沿X轴负方向走一步，到达点P2（xi+1,yi+1）。点P2的坐标由下式计算：

刀具在点P2的偏差值为

把式（4-16）代入上式，简化为

图4-9　逆圆插补的进给方向

若Fi＜0，这时刀具位于圆内，如图4-9（b）所示。为让刀具向终点B进给并靠近圆弧，应让刀具沿Y轴正向走一步，到达点P2（xi+1,yi+1）。点P2的坐标由下式计算，即

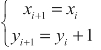
刀具在点P2的偏差值为

把式（4-16）代入上式，简化为

式（4-12）、式（4-17）和式（4-18）组成了逆圆插补偏差值的递推计算公式。

逆圆插补的计算过程如表4-6所示。(www.xing528.com)

表4-6　逆圆插补的计算过程

3.终点判别

如图4-7所示，圆弧是要加工的曲线，它的起点为A（xa，ya），终点为B（xb，yb）。加工完这段圆弧，刀具沿X轴应走|xb-xa |步，沿Y轴应走|yb-ya|步，沿两个坐标轴应走的总步数为

该公式对逆圆插补和顺圆插补都是适用的。

当插补循环数i与N相等时，即

说明圆弧已加工完毕。

4.插补程序

（1）顺圆插补。逐点比较法顺圆插补的流程图如图4-10所示。图中i是插补循环数，Fi是偏差函数，（xi,yi）是刀具坐标，N是加工完圆弧刀具沿X、Y轴应走的总步数。

开始插补时，插补循环数i等于0，刀具位于圆弧的起点A（xa,ya）。由于刀具位于圆弧上，因此偏差值F0为零。N由式（4-19）确定。

经过初始化后，程序进入“等待”状态。插补时钟发出的脉冲，使程序结束“等待”状态，继续向下运行。

接着，进行偏差判别。由表4-5可知，若偏差函数Fi大于或等于零，刀具应沿-Y方向走一步；若偏差函数Fi小于零，应让刀具沿+X方向走一步。

进给后，应计算出刀具在新位置的偏差值Fi+1及新坐标（xi+1,yi+1）。进行一个插补循环后，插补循环数应加1。

最后进行终点判别。若插补循环数i小于N，表明圆弧还没有加工完，应继续进行插补；若插补循环数i等于N，说明圆弧已加工完毕，插补工作结束。

图4-10　逐点比较法顺圆插补流程图

例4-2　如图4-11所示的是要加工的圆弧。圆弧的起点为A（3，4），终点为B（5，0）。试对该段圆弧进行插补，并画出插补轨迹。

解：加工完这段圆弧，刀具沿X、Y轴应走的总步数为

图4-11　顺圆插补轨迹

AB为顺圆插补，插补过程见表4-7。

表4-7　逐点比较法圆弧插补过程

插补轨迹如图4-11所示。

（2）逆圆插补。逐点比较法逆圆插补的流程图如图4-12所示。图中的符号与图4-10中符号的意义完全相同。

图4-12　逆圆插补流程图

例4-3　如图4-13所示的要加工的圆弧。圆弧的起点为A（5，0），终点为B（3，4）。试对该段圆弧进行插补，并画出插补轨迹。

解：加工完这段圆弧，刀具沿X、Y轴应走的总步数为

图4-13　逆圆插补轨迹

AB为逆圆插补，插补过程见表4-8。

表4-8　逐点比较法圆弧插补过程

插补轨迹如图4-13所示。

5.性能分析

（1）进给速度。如图4-14所示，P是圆弧AB上的一点，l是圆弧在P点处的切线，切线l与X轴的夹角为α。在P点附近的很小范围内，切线l与圆弧非常接近。在这个范围内，对圆弧的插补和对切线的插补，刀具速度基本相等。因此，对圆弧进行插补时，刀具在P点的速度也可用式（4-9）计算，如图4-6所示。在图4-14中，α是圆弧上P点的切线与x轴的夹角，也是连线OP与Y轴的夹角。

以上分析说明：圆弧插补中，在插补时钟保持不变的情况下，刀具的进给速度是变化的，在坐标轴附近（α≈0°或α≈90°），刀具速度最大，约为f。在第一象限的中部（α≈45°），刀具的进给速度最小，约为0.7f。刀具的进给速度的这种变化，可能对零件的加工质量产生不利的影响，加工时应注意到这个问题。

（2）加工的最大圆弧尺寸。由偏差函数的递推计算过程（表4-5和表4-6）可知，偏差函数的最大值为

图4-14　圆弧插补的速度分析

Fmax=2xi+1或Fmax=2yi+1

设Z等于圆弧起点A（xa,ya）和终点B（xb,yb）坐标中最大的一个值，即

Z=max（xa,ya,xb,yb）

因为刀具坐标（xi,yi）总是在圆弧起点和终点坐标之间变化，所以偏差函数的最大值为

Fmax=2Z+1

若偏差函数寄存器的长度有n位，把其中的最高位用于“±”号位，则偏差函数的最大允许值为

Fmax=2Z+1≤2n-1-1

由此得

Z=max（xa,ya,xb,yb）≤2n-2-1

即圆弧起点和终点坐标的最大值为2n-2-1。

由于圆弧的起点和终点坐标总小于或等于圆弧半径R，因此，在实际工作中为了方便，可按下式确定圆弧半径，即

R≤2n-2-1