CC处危险断面的应力分析

式中　m——工作条件系数，线路靠近马路m=0.8；其他线路m=0.9。

计算所得应力（σCC）不得大于附录六、附录七规定的许用应力。

【例题221】计算配电线路耐张杆横担的强度

导线型号：JL/G1A—70/10 σM=6.0kg/mm2 C=70cm

（1）截面CC的弯曲力矩，按式（221）：

MCC=σMSC=6×79.39×70=33344（kg·cm）

（2）截面CC的抗弯矩，选用100×100×1500方木横担：

选用L75×8等边角钢：

WCC=2×Wx=2×11.2=22.4（cm3）

（3）在截面CC处的应力，木横担：

L75×8角钢横担

上述所得应力都略大于横担材料的许用应力（附录六、附录七），但大的都不多。两个横担，假定是铰链连接，其变形互不影响。实际上横担的支持拉板处，都有穿心螺栓紧固，这样其变形就要互受影响，实际的抗弯矩要比计算得出的大得多。所以，TJ25型导线的耐张横担，可选用100×100×1500方木横担或选用∠75×8等边角钢横担。

上边我们把两个横担安装在电杆两侧组合而成的耐张横担，当作两个横担是铰链连接，其变形都以自己的中心线为中性层而变形，互不影响。其实这种假设偏于保守，实践证明这两个横担是互受影响的。下边我们补充研究一下，如果组合横担的连接相当牢固，像一个正体。变形时中性层就是（x-x）aa′横担受拉，bb′横担受压，这样，可以利用平行轴惯性矩定理来计算它的抗弯矩。

现在用式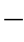（22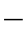3）校验一下【例题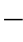22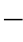1】所选横担的抗弯矩。

（1）100×100×1500方木组合横担的抗弯矩（图222）：

Jx=2（Ix1+Fd2）(www.xing528.com)

=2（833.3+100×12.52）

=32917（cm4）

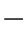式中　=833.3（cm4），（计算公式见表341）；

F=a2=102=100（cm2）；

d=12.5cm。

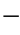图22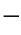2　方木组合横担

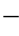图223　角钢组合横担断面

（2）∠75×8等边角钢组合横担的抗弯矩（图223）：

Jx=2（Ix1+Fd2）=2（59.96+11.5×14.352）=4856.1（cm4）

式中　Ix1=59.96cm4；

F=11.5cm2；

d=14.35cm。

从计算结果可以看出，两种方法所得之组合横担的抗弯矩WCC值是不一样的，而且相差很大。

实际上，WCC值处于两种计算方法所得值之间，其大小与横担螺栓紧固程度有关。我们现在所使用的不加斜材的组合横担，因支持拉板处加了个穿心螺丝，把两个横担牢牢的连在一起。可以认为，在固定螺栓至电杆一段是一体，其以xx轴为中性层而变形，固定螺丝至横担头，可以认为是铰链连接，校验固定螺栓（固定支持拉板螺栓）处的横担强度。