钢心铝线的弹性与膨胀特性对比

导线的弹性系数和线膨胀系数是弧垂计算的重要数据。那么，像钢心铝线这样的组合导线，又将怎样来采用呢？下面就予以论述。

首先，假定钢心铝线的总截面为S，铝及钢心的截面分别为SL及SG。并且假定铝和钢的弹性系数为EL和EG，整个钢心铝线的等值弹性系数为E。假定导线承受拉力时，各股导线之间没有滑动而且同样伸缩，同时铝及钢心所承受的拉力都未超过弹性极限分别为TL及TG。因为T=TL+TG，S=SL+SG，每股导线的伸长率相等，所以：

令=m，上式可改写为：

式（1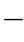215）是钢心铝线这类组合导线的等值弹性系数的计算式。

其次，假定铝线的线膨胀系数为αL，钢线为αG，整个钢心铝线的等值线膨胀系数为α，αL大于αG，因为α在αL和σG之间，所以，由于温度上升，单股铝线要比置于组合导线中的本身伸长要长一些，相反的钢线要比在组合导线中的钢心伸长要短一些。这也就是说如果温度大于导线制造时的温度，铝的拉力减小钢心的拉力增加。现在假定比导线制造时温度上升θ℃，根据上述理由，铝的应力减小为σL，钢的应力增加为σG，因为铝线部分的伸长必须等于钢心部分的伸长，所以：

由于整个绞线的荷重未变，所以：

整个钢心铝线因温度而产生的伸长，根据上式得知为：(www.xing528.com)

所以整个钢心铝线的线膨胀系数为：

以上是假定应力平均作用在整个截面上的计算式。也就是说，两种导线的单位截面所分担的拉力决定于弹性系数的比值。但是，钢心线和铝线的弹性系数的比值为21∶63=10∶30，弹性极限的比值为（70～95）∶9.8≈10∶（1～1.5）左右，弹性极限对分担拉力的比值铝线是非常大的。即假定在两种金属之间没有滑动并且同样伸缩，整个钢心铝线的弹性极限为较低的铝线弹性极限所控制，这样，为了使其具有机械强度而采取钢心线的意义就变得非常奇怪。

在发现制造钢心铝线以前，关于是否可以将弹性系数。弹性极限和线膨胀系数具有这样差别的两种金属绞和在一起使用，好像在技术上是个重大问题。然而尽量使钢心线和铝线所承担的拉力更为合理，又对面积比例和绞合方法进行了研究，就完成了钢心铝线的制造。由于制造时采取适当的绞线方法，所以，像钢心线这样弹性系数高的导线的绞捻程度，能越来越紧，像铝线这样弹性系数低的导线能保持绞后的原状，即不再松散，也不再过紧。如将拉力加在这样的导线上，首先，钢心部分承受拉力，随着绞线变紧，铝线部分才承受拉力。适当调整绞捻的程度，使导线分别承担最合理的拉力，这是导线制造技术上需要大费心机的地方。

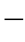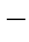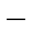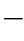严格地来讲，铝线的应力——应变曲线的起点，比钢心铝线的起点稍往右方错开了一些，推导式（1215）和式（1216）所使用的“应力平均作用”的假定是有疑问的。因为在实际计算弧垂时，所遇到的导线拉力都相当大，所以，也允许这个近似的假定。通常使用式（1215）和式（12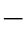16）进行计算，是没有什么大问题的。

以上将钢心铝线作为组合导线的代表作了说明。对于其他组合导线，例如，铜包钢线等，可以认为式（1215）和式（1216）也同样是成立的。