式(1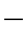 2
2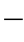 2)告诉我们,只要知道导线跨度l、比载g及导线最小拉应力σ0就可以求出弧垂f。但是,在周围空气温度、风力负荷、冰层负荷变化的影响下导线的应力、弧垂必然要变化。现在就是要找出综合这些可变因素的方程式。为了得到这个关系式,需要相当繁琐的数学演算,不易得到明确的概念。现在作比较直观的研究:
2)告诉我们,只要知道导线跨度l、比载g及导线最小拉应力σ0就可以求出弧垂f。但是,在周围空气温度、风力负荷、冰层负荷变化的影响下导线的应力、弧垂必然要变化。现在就是要找出综合这些可变因素的方程式。为了得到这个关系式,需要相当繁琐的数学演算,不易得到明确的概念。现在作比较直观的研究:
图1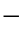 2
2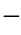 2 导线总长度
2 导线总长度
从式(1 2
2 5)L总=
5)L总=![]() ,或L总=
,或L总=![]() 中看到,导线总长度有两项(图1
中看到,导线总长度有两项(图1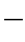 2
2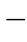 2)第一项l是A、B间直线距离;第二项
2)第一项l是A、B间直线距离;第二项![]() 是由于有了弧垂,直线变成了曲线而增加的那一部分长度。自然要问增加的这部分长度是由什么引起的。回答是导线内有拉应力σm,或温度上升均可使导线变长。现在就来计算一下这两种伸长。
是由于有了弧垂,直线变成了曲线而增加的那一部分长度。自然要问增加的这部分长度是由什么引起的。回答是导线内有拉应力σm,或温度上升均可使导线变长。现在就来计算一下这两种伸长。
由于拉应力引起的伸长:Δ1=lβσm,由于温度变化θm℃的伸长:Δ2=lαθm,导线的总伸长量:Δl=Δ1+Δ2=lβσm+lαθm。就是这个伸长量使导线由直线变为曲线。但曲线比直线长![]() 所以:
所以:
图1 2
2 3 导线实际状态
3 导线实际状态
式(1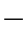 2
2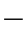 6)可用图形直观地说明,把图1
6)可用图形直观地说明,把图1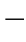 2
2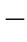 3(b)中曲线放平直,就成了图1
3(b)中曲线放平直,就成了图1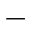 2
2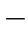 3(a)的情况。式(1
3(a)的情况。式(1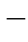 2-6)两边除以β、l将得:
2-6)两边除以β、l将得:
对于另一种空气条件:温度为θn,比载为gn时,可以重复这种论证过程得到同样的公式:
式(1 2
2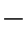 8)减去式(1
8)减去式(1 2
2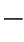 7),并经移项整理就得到:
7),并经移项整理就得到:
式中 σm——导线最大许用应力;
σn——在温度为θn℃和比载为gn时的应力,kgf/mm2;
α——导线材料温度膨胀系数,1/℃;
β——导线材料弹性伸长系数,1/kg/(mm2·m);
E——弹性系数;
l——档距,m;(https://www.xing528.com)
gm——导线最大应力时的比载,kgf/(mm2·m);
当实际档距大于临界档距时,“0”气象区gm=g6;“Ⅱ~Ⅸ”气象区gm=g7;当实际档距小于临界档距时,所有气象区gm=g1;
gn——给定的导线比载,kgf/(mm2·m);
当计算不覆冰的导线弧垂时,gn=g1;
当计算覆冰的导线弧垂时,gn=g3;
当计算最大荷重时的弧垂时,“0”气象区gn=g6,“Ⅱ~Ⅸ”气象区当g7>g6时gn=g7;当g7<g6时,gn=g6;
θm——起始温度:
当gm=g6时,θm=+10℃;
当gm=g7时,θm=-5℃;
当gm=g1时,θm=最低温度。
θn——给定温度。
式(1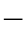 2
2 9)就是有名的导线状态方程;即只要知道了一种状态下的导线情况,那么,当条件变化成任何一种情况,均可以通过式(1
9)就是有名的导线状态方程;即只要知道了一种状态下的导线情况,那么,当条件变化成任何一种情况,均可以通过式(1 2
2 9)计算出来。具体地说,如果温度为θm和比载为gm时,导线应力σm已知,即可根据上式求出温度为θn比载为gn时导线的应力σn,然后就可按式:
9)计算出来。具体地说,如果温度为θm和比载为gm时,导线应力σm已知,即可根据上式求出温度为θn比载为gn时导线的应力σn,然后就可按式:
求出导线弧垂。如前所述,导线所形成的曲线为一悬链线方程式,由于双曲线函数的计算非常繁杂,所以,在许多情况下把悬链线近似地当作抛物线进行计算。这样,当弧垂不大于档距的10%时,按抛物线考虑的近似计算法所引起的误差是很小的。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




