弧垂与导线拉力的关系探析

现在我们讨论一下弧垂与导（地）线内部各点应力的关系。设导线悬挂在A、B两点上，A、B在同一水平面上，跨距为l，弧垂为f[图121（a）]。若导线是一根理想柔软而且负荷均匀的线通过较复杂的数学推演，可以得到导线的曲线方程为一悬链方程。但是，我们最感兴趣的是弧垂与导线内各点应力的关系。因为，在实践中知道，跨距l要比弧垂f大得多。在此情况下，可以假设导线的负荷沿跨度（而不是沿曲线）是均匀的，这种假设实际误差很小，已能满足工程需要。在这种条件下，导线不是悬链线而是抛物线。

设G为单位跨度上导线负荷（kg/m）。为了讨论导线内各点的应力，采用截面法，曲线是对称的，故只讨论半边就行了。截取OC这一段，见图121（b）其上的作用力：TO为O点水平拉力，TC为C点拉力，Gx为OC段的重力。从图中可以直观地看出，OC这段线处于平衡时，TC的水平分力必须与TO平衡，TC的垂直分力与重力Gx平衡。用平衡方程表示：

图121　导线内各点应力计算

从式（12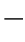1）中可以得出结论，导线上各点的拉力是随x变化的，x=0时，即在O点处（最低点）导线的拉力最小，时，即B点（或A点）处拉力最大（悬挂点）。现在就来研究最大或最小拉力与弧垂之间的关系。截取OB段[图1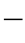21（c）]，此线段是在三力：水平拉力TO、重力及悬挂点拉力TB作用下处于平衡。故可用平衡方程对B点取力矩：

并注意到：

式中　g——导线比载，kg/（mm2·m）。

那么就得：

这样，我们就得出了最小（导线最低点）应力、跨度与弧垂之间的关系。现在我们来求导线最大应力。根据图1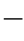2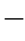1（c）中各力对水平轴和垂直轴列平衡方程：

由直角关系：(www.xing528.com)

用代入即得到：

因很小，可用近似公式

两边除以截面积S：

由于两悬挂点等高，所以σA=σB，故可写成σA=σB=σ0+gf。

式（124）告诉我们，悬挂点处（最大）拉应力等于导线最低点处（最小）拉应力加上弧垂与比载的乘积。

但是，在计算导线拉应力时，只计算导线最低点的拉应力（σ0）而不去计算导线悬挂点的拉应力（σA或σB），这是因为一般情况下，导线弧垂f值不大，g·f值很小，可以忽略；而对档距很大的线路，f值较大，g·f值不能忽略。因此，应对导线悬挂点的拉应力进行校验。

下边我们研究导线的总长度L总。很明显，由于导线在A、B两悬挂点间不是直线，故总长度要比跨距大些，其大小与跨矩l、弧垂f及曲线形状有关。如果导线是抛物线，通过数学运算（即进行线积分）就可求出：

从式（125）中，可以清楚地看出，跨距l越大，弧垂f越大时，导线长度L总越大。