1.功率
力在单位时间内所做的功称为功率,功率表明力做功快慢的程度,以P表示。
功率的数学表达式为
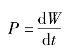
功率单位是W(瓦特),1W=1J/s。
1)力的功率
由于力F在微小路程ds上所做的元功为dW=Fcosαds,因此,力的瞬时功率为

式(4-2-19)表明,力的瞬时功率等于该力在其作用点速度方向上的投影与速度的乘积。式中,α为力与速度方向的夹角。若α=0,即力的方向与速度方向一致,则
![]()
2)力矩的功率
由于力偶矩M在微小角位移dφ中所做的元功为dW=Mdφ,因此,转矩的瞬时功率为
![]()
式(4-2-20)表明,力矩的瞬时功率等于力偶矩与转动物体角速度的乘积。
由式(4-2-19)和式(4-2-20)可以看出,当功率一定时,F与v成反比,或M与ω成反比。例如,汽车上坡时需要较大的驱动力偶矩M或较大的牵引力F,驾驶员需用低速挡,使汽车的速度减小,以便在一定功率的情况下产生较大的牵引力。
工程中常给出转动物体的转速n(r/min),力矩M(N·m),功率P(kW),它们之间的关系可由下式换算:

2.功率方程
取构件系统动能定理的微分形式dE=∑dW,两端除以dt,得
![]()
式(4-2-22)表明,物系动能随时间的变化率等于作用于物系的所有力的功率的代数和。
功率方程常用来研究机器工作时能量的变化和转化的问题。例如,车床接通电源后,电场给转子作用的力做正功,使转子转动,电场力的功率称为输入功率。由于皮带、齿轮传动和轴与轴承之间都有摩擦,摩擦力做负功,使得一部分机械能转化为热能;在传动系统中,零件之间会发生相互碰撞,这也会造成损失一部分功率。这些功率都取负值,称为无用功率或损耗功率。车床切削工件时,切削阻力对工件做负功,这是车床加工零件所必须付出的功率,称为有用功率或输出功率。
每台机器的功率都可分为输入功率、无用功率和有用功率。一般情况下,式(4-2-22)可写成
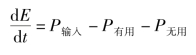
或写成

式(4-2-23)称为功率方程,方程表明:系统的输入功率等于有用功率、无用功率和系统动能的变化率的和。
3.机械效率
每台机器在工作时都要从外界输入功率,其工作时由于一些机械能转化为热能、声能等,都将消耗一部分功率。在工程中把有效功率与输入功率的比值称为机器的机械效率,用η表示,即

因此可见,机械效率η表示了机器对输入功率的有效利用程度,它是评价机器质量好坏的重要指标。一般机械的机械效率可在设计手册中查到。
例4-2-3 如图4-2-11所示,单级齿轮减速箱P=7.5kW,转速n1=1450r/min,齿轮齿数z1=15,z2=20,减速箱的机械效率η=0.85。试求输出轴Ⅱ所传递的力矩和功率。
解:由机械效率公式(4-2-24)可求得输出轴Ⅱ的功率为
![]()
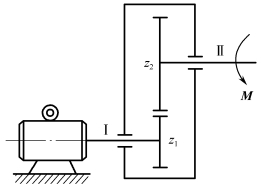
图4-2-11 例4-2-3图
输出轴Ⅱ转速为
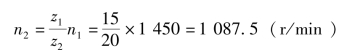
根据式(4-2-21)可得输出轴Ⅱ所传递的力矩
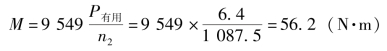
【任务实施】
如图4-2-1所示,自动送料机构的小车与货物的质量为m1,鼓轮的质量为m2,半径为r1,轨道的倾角为α,鼓轮上作用一不变的力矩M,不计摩擦和鼓轮的质量。求小车由静止开始沿轨道上升路程s时的速度。
解:(1)受力分析。系统受到小车的重力G1=m1g,鼓轮的重力G2=m2g,斜面的支持力N1、N2,鼓轮上的力矩M。
(2)计算系统的动能。初始位置时小车静止,所以系统的动能E1=0,沿斜面运动s后的动能
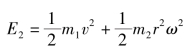
将ω=![]() 代入上式得(https://www.xing528.com)
代入上式得(https://www.xing528.com)
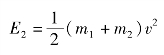
(3)计算主动力的功。主动力所做的功为鼓轮力矩的功与小车的重力的功之差,即
![]()
将φ=![]() 代入上式,得
代入上式,得
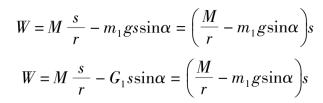
由式(4-2-13)E2-E1=∑Wi,得
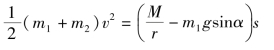
解得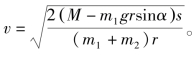
【任务小结】
1.质点的动静法
(1)惯性力:![]()
(2)达朗伯原理:
![]()
(3)动静法的自然坐标式:
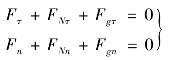
(4)动静法的直角坐标式:
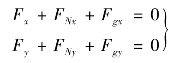
2.功
(1)质点动能定理的积分形式:
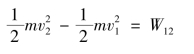
(2)力的功:
①常力的功:
![]()
②重力的功:
![]()
③弹性力的功:
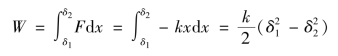
④常力矩的功:
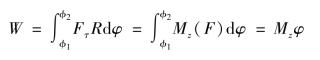
3.动能定理
(1)质点的动能:
![]()
(2)平动构件的动能:
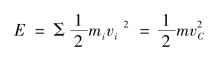
(3)定轴转动构件的动能:
![]()
4.功率方程与机械效率
(1)力的功率:
![]()
(2)力矩的功率:
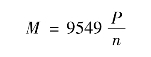
(3)功率方程:
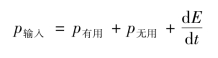
(4)机械效率:
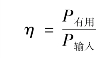
【实践训练】
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




