质点动能定理的微分形式：力量即功

1.力的元功

设质量为m的质点，在大小和方向都不变的力F作用下，沿直线走过一段路程s，力F在这段路程内所积累的效应用力的功来量度，以W来表示，并定义为

式中　θ——力F与直线位移方向之间的夹角。

功是标量，其单位为J（焦耳），1J＝1N·m。

设质量为m的质点，在任意变力F作用下沿曲线运动，如图4-2-5所示。力F在无限小位移dr中可视为常力，经过的一小段圆弧ds可视为直线则在一无限小位移中作用的功称为元功，以dW来表示。

因此有

由质点动力学基本方程的自然坐标式知

在上式两边同乘以微段路程ds得

图4-2-5　力的元功

式中，mv2为质点的动能。于是得到质点动能定理的微分形式

式（4-2-7）表明，质点动能的微分等于作用在质点上力的元功。

如果质点从S1运动到S2，其速度由v1变为v2，质点运动的路程为s＝S2-S1。对式（4-2-7）进行积分运算，则

即得质点动能定理的积分形式

式（4-2-8）表明，在质点运动的某个过程中，质点动能的改变量等于作用于质点的力所做的功。

需要说明的是，动能是描述质点运动强弱的物理量。而功是力在一段路程中对物体作用的积累效应，其结果使质点的动能发生了变化。力做正功，质点的动能增加；力做负功，质点的动能减小。动能的改变是用功来度量的。

2.力的功

力的功表征了力在其作用点的位移上对物体的积累效应。下面讨论常见的几种力所做功的计算。(www.xing528.com)

1）常力的功

设质量为m的质点在大小、方向不变的常力F的作用下沿水平直线运动，力F与运动方向的夹角为α，质点在力F的作用下从S1运动到S2的直线位移为s，如图4-2-6所示。将力F沿速度方向和垂直于速度方向分解为分力Fx和Fy，因质点是沿水平方向运动，故只有水平分力Fx才使质点改变运动状态，垂直分力Fy对质点的水平运动没有影响。因此，我们把力F在速度方向的投影Fcosα与位移s的乘积，称为力F在位移s上对质点所做的功。以W表示，即

由式（4-2-9）可以看出：当α＜90°时，力做正功；当α＞90°时，力做负功；当α＝90°时，力不做功，即W＝0。

2）重力的功

设一质点重为G，其沿一条曲线轨迹由S1运动到S2，如图4-2-7所示，则重力G所做的功为

式（4-2-10）中，h表示质点的起始点与终点的位置之高度差。显然，质点下落时，重力做正功；质点上升时，重力做负功。

式（4-2-10）表明，重力的功等于质点的重量与起始位置和终了位置高度差的乘积。与质点的运动路程无关。

图4-2-6　常力的功

图4-2-7　重力的功

3）弹性力的功

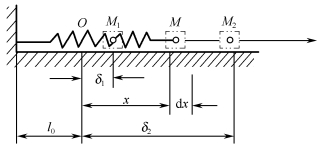
图4-2-8　弹性力的功

图4-2-8所示的弹簧一端固定，另一端系住做水平直线运动的物块M（可简化为质点）。设弹簧原长为l0，当弹簧处于原长时质点所在的位置O称为自然位置。当质点偏离自然位置使弹簧产生拉伸或压缩时，弹簧将对质点作用一弹性力F，该力总是企图使质点回复到自然位置，因此弹性力的方向恒指向自然位置O，即弹性力的方向与伸长（或缩短）的方向总是相反。当弹簧的变形在弹性范围内时，由物理学知，弹性力的大小与弹簧的变形量成正比，即F＝-kx，k为弹簧的刚性系数，其单位为N/m。当质点正向移动一微段距离dx时，弹性力的元功为dW＝-kxdx。若物块从M1运动到M2位置，即伸长量由δ1增至δ2过程中，弹性力所做的功为

图4-2-9　常力矩的功

式（4-2-11）表明，弹性力的功等于弹簧初变形的平方与末变形的平方之差乘以弹簧刚性系数的一半。当初变形大于末变形时，弹性力做正功；当初变形小于末变形时，弹性力做负功。弹性力的功只与弹簧的始末变形有关，而与质点运动的轨迹形状和路程长度无关。

4）常力矩的功

如图4-2-9所示，设质点A在力F的作用下绕z轴转动，力F的作用线在A点轨迹的切平面内与切线夹角为α，则力F在切线的投影为Fτ＝Fcosα，A点轨迹曲线ds＝Rdφ。因此力F在质点轨迹曲线上所做的元功为dW＝Fcosαds＝Fτds＝Fτdφ＝Mz（F）dφ，若Mz（F）为常力矩，因此常力矩的功为

式（4-2-12）表明，作用于定轴转动构件上常力矩的功等于力矩的大小与转角的乘积。当力矩转向与转角同向时，力矩做正功；反之做负功。