构件定轴转动的动力学基本方程优化为：构件定轴转动力学基本方程

1.刚体转动动力学基本方程

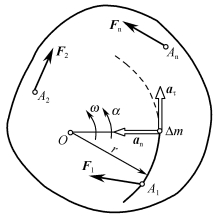
图4-1-7　刚体转矩和角加速度的关系

设质量为m的刚体，在F1，F2，…，Fn诸力作用下，绕定轴O转动，这些力分布在与定轴垂直的平面内，如图4-1-7所示。各力对轴O的力矩的代数和为∑mO（F）＝M，M统称为转矩。在转矩作用下，刚体做变速转动，下面讨论转矩和角加速度之间的关系。

设某瞬时刚体转动的角速度为ω，角加速度为ε。因为刚体可以看成是由无数质点所组成，取其中任一质点，设其质量为Δm，离定轴O（亦称转轴）的距离为r（亦称转动半径）。当刚体绕定轴O转动时，该质点做变速圆周运动，由运动学知，质点的切向加速度aτ＝rε，其指向与角加速度转向相同，法向加速度为an＝rω2，并指向转动中心。

由质点动力学基本方程知，作用在该质点上的切向力Fτ与aτ同向，大小为

其法向力为

切向力对转轴之矩为

其转向与α相同；法向力对转轴之矩为

对应于刚体内的每一质点，均可写出与上述形式相同的式子。从整个刚体来看，作用在刚体上的转矩必等于使刚体内各质点获得加速度的各力对转轴之矩的代数和。即

式中，∑Δmr2称为刚体对转轴的转动惯量，通常用符号J来表示，则

于是可得

式（4-1-4）称为刚体转动动力学基本方程。它表明：当刚体绕定轴转动时，作用在刚体上的各力对转轴的矩的代数和（即转矩）等于刚体对该轴的转动惯量与其角加速度的乘积。角加速度的转向与转矩的转向相同。利用上式可解决刚体转动动力学的两类基本问题：已知转矩求角加速度和已知角加速度求转矩。

2.转动惯量

1）转动惯量的概念

图4-1-8　飞轮

由上述可知，转动惯量J＝∑Δmr2。式中∑Δmr2是刚体中每一质点的质量（Δm）与该质点转动半径（r）的平方的乘积的总和。这个总和为该刚体对转轴的转动惯量，其单位可根据质量单位和长度单位导出，通常为千克·米2（kg·m2）。

由转动惯量的定义可知，转动惯量恒为正值。它的大小不仅与刚体质量的大小有关，而且与质量的分布有关。当刚体质量一定时，这些质量分布离转轴愈近，则转动惯量愈小；反之则愈大。机器上常用的飞轮（见图4-1-8），常做成边缘厚中间薄，就是为了将大部分材料分布在远离转轴的地方，以增大转动惯量。

从式（4-1-4）可以看出，当作用在刚体上的转矩M一定时，转动惯量J大的刚体，它的角加速度ε就小。角加速度ε小，说明刚体不容易改变原有的转动状态，这就表明刚体的转动惯性大。反之，转动惯量J小的刚体，角加速度ε就大，表明它易于改变转动状态，即它的转动惯性小。所以转动惯量是刚体对转轴转动惯性的度量。

2）简单形状物体的转动惯量

由转动惯量的表达式J＝∑Δmr2可知，当把刚体看做是由无数质点组成时，则此刚体的转动惯量就等于无限多个质点的转动惯量的总和的极限值，用积分形式表示，即为

下面以匀质圆柱（或圆盘）对中心轴的转动惯量为例来说明转动惯量的计算。

如图4-1-9所示，设半径为R长为l的匀质圆柱[见图4-1-9（a）]，质量为m。取一离转轴距离为r厚度为dr的微分圆筒，其体积为

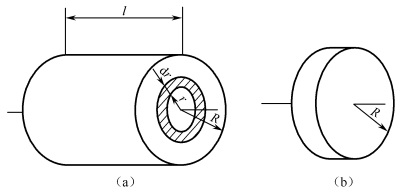
图4-1-9　物体的转动惯量

(https://www.xing528.com)

而整个圆柱体的体积为

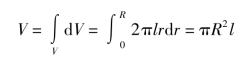
因而微分圆筒的质量为

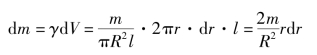
于是整个圆柱对中心轴的转动惯量为

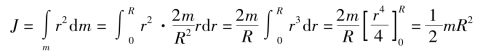
结果表明，转动惯量与圆柱的长度l无关，所以圆盘可看做长度很小的圆柱[见图4-1-9（b）]，即上述公式对圆盘仍然适用。

工程上常将刚体的转动惯量J设想为刚体的总质量m与某一长度ρ的平方的乘积，即

长度ρ称为惯性半径（亦称回转半径）。惯性半径相当于将刚体的总质量集中于某点，若该质点绕转轴旋转时其转动惯量与原刚体对同一轴的转动惯量相等，则该质点与转轴的垂直距离称为刚体对此轴的惯性半径，必须指出，惯性半径为一抽象概念，一般它与转动刚体的几何尺寸并不一致。

只要由有关手册中查出惯性半径，利用式（4-1-6），就很容易算出刚体的转动惯量。

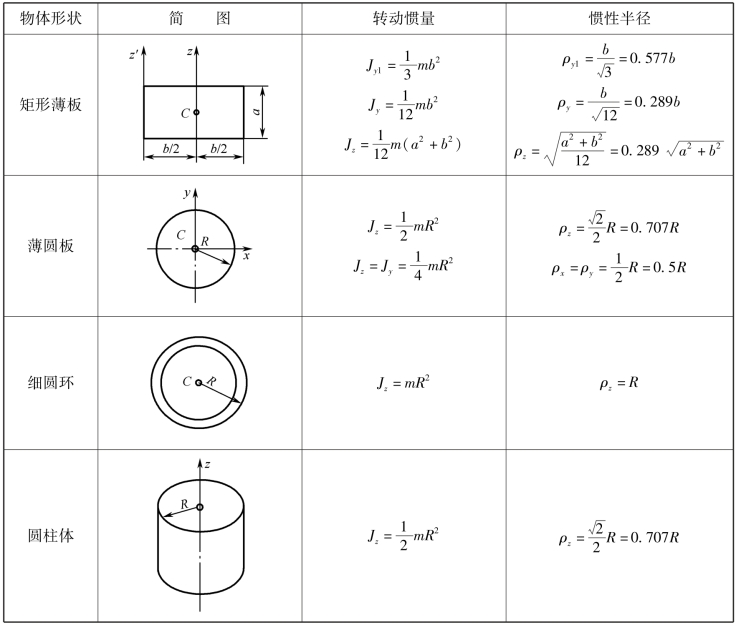
常用简单形状物体的转动惯量见表4-1-1。

表4-1-1　常用简单形状物体的转动惯量

续表

3）转动惯量的平行轴定理

物体对于不同的转轴将有不同的转动惯量，对于各种简单形体，在表4-1-1中（或工程手册中）只能查到它们对于通过重心轴的转动惯量，可是在工程实际中有时转轴并不通过重心，但与重心轴平行，下面讨论物体对于两个平行轴的转动惯量之间的关系。

设z轴通过物体的重心O，物体对于这轴的转动惯量为Jz。物体对于与z轴平行且相距为d的z1轴的转动惯量可用下面的方法求出。

通过重心O取互相垂直的坐标轴x、y、z，并使y轴与z1轴交于O1点，过O1取另一垂直坐标系x1、y1、z1（y轴与y1轴重合），如图4-1-10所示，则坐标之间的关系为

物体对于z1轴的转动惯量为

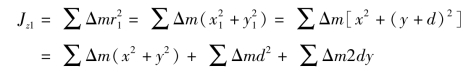
又

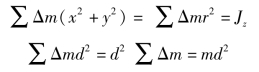
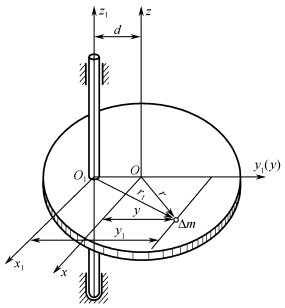
图4-1-10　转动惯量的平行轴定理

由质心C的坐标xC＝yC＝0可知

故有

即物体对任意轴z1的转动惯量Jz1等于对通过重心且与z1平行的z轴的转动惯量Jz；再加上物体的质量m与两平行轴间距离平方的乘积。这种关系称为转动惯量的平行轴定理。

需要指出，因为md2总是正值，故Jz1总是大于Jz。可见，在物体对于所有平行轴的转动惯量中，以物体对于其重心轴的转动惯量为最小。