构件平面运动的特点及其力学模型分析

1.工程实例与力学模型

如图3-2-9（a）所示，车轮沿直线轨道滚动时，既不是平动又不是定轴转动，但其上某一平面，在运动过程中始终与一固定平面保持平行；如图3-2-9（b）所示，曲柄滑块机构中连杆AB的运动，又如图3-2-9（c）所示，行星轮系中行星轮A的运动，既不是平动又不是定轴转动，但构件上某一平面，在运动过程中始终与一固定平面保持平行。

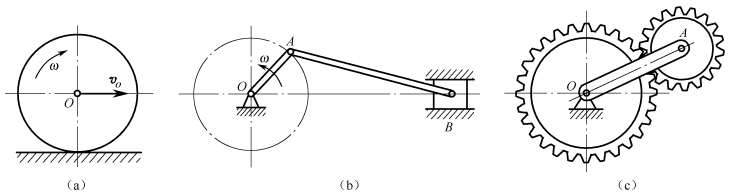
图3-2-9　刚体的平面运动

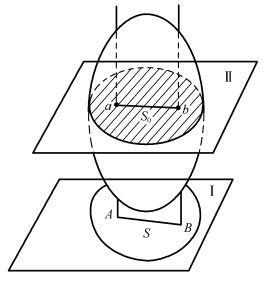
图3-2-10　做平面运动的刚体

图3-2-9（a）、（b）、（c）分别为车轮的平面力学模型、连杆机构的平面力学简图和行星轮系的平面力学模型。它们的共同特点是：构件在运动时，既不是平动又不是定轴转动，但其体内某一运动平面与一固定平面始终保持平行，这种运动称为构件的平面运动。

根据构件平面运动的特点来建立构件平面运动的力学模型，为使问题得到简化，通常将做平面运动的构件，在所选的固定参考平面Ⅰ内进行投影，用构件的投影轮廓线来代替构件，建立起构件平面运动的平面力学简图。如图3-2-10所示，设Ⅰ为一固定参考平面，刚体内各点到该平面的距离保持不变。用一平行于Ⅰ平面的平面Ⅱ切割刚体，得刚体的截平面S0，为构件内的某一运动平面；运动平面S0内任意两点a、b的连线ab的运动，可表示为AB连线在固定参考平面Ⅰ内的运动。

因此，构件的平面运动，可以简化为平面图形S在其所选固定参考平面内的运动。此即为构件平面运动的力学模型。

2.平面运动分解为平移和转动

设平面图形在它所在的平面内运动，在该平面内取定坐标系Oxy如图3-2-11所示。任意瞬时平面图形的位置可由图形内任意线段AB的位置来确定，而线段AB的位置可由A点的坐标x、y及线段AB与x轴的夹角φ决定。当图形运动时，它们都是时间的单值连续函数，即

式（3-2-2）称为刚体平面运动的运动方程。其中任意选定的A点称为图形的基点，角φ的符号规定与定轴转动时的转角φ相同。(www.xing528.com)

若x、y不变，即A点保持不动，则图形做定轴转动；若φ不变，即线段AB始终与其原来的位置平行，则图形做平移。因此，平移和定轴转动是平面运动的两种特殊情形。在一般情况下，平面运动可看做是平移和转动的合成。

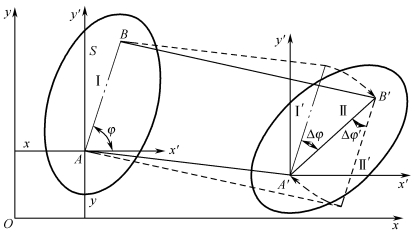
图3-2-11　构件平面运动分析

在工程上研究刚体的平面运动常用的方法是应用合成运动的概念，通过选定一个适当的动参考系，把平面图形对于定参考系的绝对运动（平面运动），分解为随同动参考系的牵连运动和相对动参考系的相对运动。

设平面图形S做平面运动，其位置可由图形S内任一线段AB的位置来确定。选固定在地面上的参考系Oxy为定系，选固定在平面图形S上的参考系Ax′y′为动系，设A点为基点，如图3-2-11所示。

经过时间间隔Δt，AB由位置Ⅰ运动到位置Ⅱ。上述运动可作如下分解：

（1）线段AB随同固连于基点A的动系Ax′y′做平移至I′位置；

（2）绕点A′转过Δφ角到达最终位置Ⅱ，即A′B′。

当然，实际上上述平移与转动是同时进行的，只是当Δt取得越小，这种分解越接近真实的运动情况。需要强调的是当线段随基点A做平移时，整个图形上的点都做了相同的平移。基于这样的事实，便引进平移坐标系以实现对平面运动的分解。

由此可见，平面图形的运动（即构件的平面运动）可以分解为随同基点的平动（牵连运动）和绕基点的转动（相对运动）。

这里应该特别指出，平面图形的基点选取是任意的。从图3-2-11中可知，选取不同的基点A和B，平动的位移是不相同的，即，显然vA≠vB，同理，aA≠aB。所以，平动的速度和加速度与基点位置的选取有关。

选不同的基点A和B，转动的角位移是相同的，即Δφ＝Δφ′，显然，ω＝ω′，同理，ε＝ε′。即在同一瞬时，图形绕其平面内任选的基点转动的角速度相同，角加速度相同。平面图形绕基点转动的角速度、角加速度分别称为平面角速度、平面角加速度。所以，平面图形的角速度、角加速度与基点的选取无关。