如图3-2-5所示,设运动平面S上有一曲线槽AB,槽内有动点M沿槽运动,定参考系Oxy固连在地面上,动参考系O′x′y′固连在运动平面S上。任意瞬时t,动点位于动系O′x′y′的M处,经过时间间隔Δt后,曲线槽随同动系运动到A′B′位置,而动点M也沿曲线槽运动到M″,所以动点M相对于定系的绝对运动轨迹为![]() ,则动点M相对于定系的绝对位移为
,则动点M相对于定系的绝对位移为![]() ;动点M相对于动系的相对运动轨迹为
;动点M相对于动系的相对运动轨迹为![]() ,相对于动系的相对位移为
,相对于动系的相对位移为![]() ;动系相对于定系的轨迹为
;动系相对于定系的轨迹为![]() ,牵连位移为
,牵连位移为![]() 。由图可见
。由图可见
![]()
将上式两边除以时间间隔Δt,令Δt→0时取极限,得M点的速度为
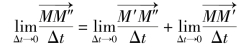
式中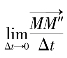 ——动点相对于定系的瞬时速度,称为绝对速度,用va表示,方向沿
——动点相对于定系的瞬时速度,称为绝对速度,用va表示,方向沿![]() 的切线方向;
的切线方向;
![]() ——动点相对于动系的瞬时速度,称为相对速度,用vr表示,方向沿
——动点相对于动系的瞬时速度,称为相对速度,用vr表示,方向沿![]() 的切线方向;
的切线方向;
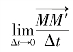 ——动点与动系重合点相对于定系的速度,称为牵连速度,用ve表示,方向沿
——动点与动系重合点相对于定系的速度,称为牵连速度,用ve表示,方向沿![]() 的切线方向。
的切线方向。
因此,上式可写为
![]()
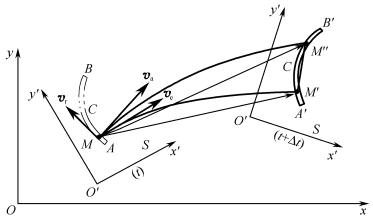
图3-2-5 点的速度合成
此式表明,动点的绝对速度等于它的牵连速度与相对速度的矢量和,即动点的绝对速度可以由相对速度和牵连速度为邻边组成的平行四边形的对角线表示,即为点的速度合成定理。
速度合成定理所表示的矢量方程,共包含有6个量(绝对速度、相对速度、牵连速度的大小和方向),若已知其中4个量,便可以求出其余的两个未知量。
应用速度合成定理求解实际问题时,要注意正确选取动点和动系,分清三种运动和三个速度,再根据已知条件作出速度矢量图,然后应用几何关系或矢量投影式解出未知量。
例3-2-1 船A以匀速v1向正东方向航行,船B向东偏北α角方向匀速航行,船B在船A的正北方,如图3-2-6所示。求船B的速度v2和在船上观察到的B的速度。
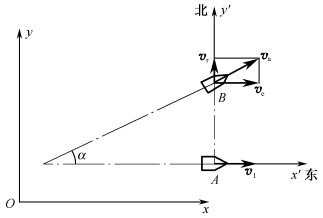
图3-2-6 两船的相对速度
解:(1)选取动点和动系。选取固定在地面上的参考系Oxy为定系,选固定在A船上的参考系Ax′y′为动系,取船B为动点。
(2)运动和速度分析。动点B的绝对运动为沿航线的直线运动,速度va=v2,与x轴成α角方向;由于船B在船A的正北方,所以动点B的相对运动为沿Ay′方向的直线运动,速度为vr;牵连运动为A船沿x′轴的直线运动,速度ve=v1。
(3)用速度合成定理,由式(3-2-1)作速度矢量图,如图3-2-6所示。
由图可知
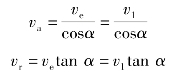 (https://www.xing528.com)
(https://www.xing528.com)
例3-2-2 仿形铣床如图3-2-7所示,当靠模A以速度v1向右移运动时,推动探针MN沿铅垂方向运动,图示瞬时角θ已知,试求该瞬时探针的速度。
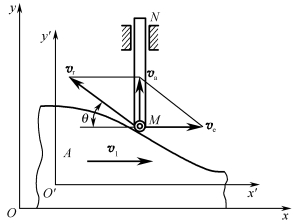
图3-2-7 仿形铣床
解:(1)选取动点和动系。探针上的端点M为动点,动系O′x′y′固连在靠模上;定系Oxy固连在地面上。
(2)运动和速度分析。动点M随探针所做的上下直线运动为绝对运动,速度为va;动点M沿靠模表面的曲线运动为相对运动,速度为vr;靠模A向右做的直线平动为牵连运动,速度为ve,ve=v1。
(3)根据速度合成定理,由式(3-2-1)作速度矢量图,即速度合成的平行四边形如图3-2-7所示。
由图中几何关系得
![]()
例3-2-3 在图3-2-8所示的刨床摆动导杆机构中,已知曲柄长OA=r,并以匀角速度ω转动,两转动轴的距离OO′=l。当曲柄在水平位置时,求摇杆的角速度ω1。
解:(1)选取动点和动系。运动时曲柄OA绕O轴转动时,滑块A在导杆的槽中滑动,通过滑块A带动导杆O′A绕O′轴摆动。所以选固定在地面上的参考系O′xy为定系,固定在摇杆上的参考系O′x′y′为动系,取滑块A为动点。
(2)运动和速度分析。动点A随曲柄OA做半径为r的圆周运动为绝对运动,速度为va;滑块A沿摇杆滑道的往复直线运动为相对运动,速度为vr;摇杆绕O′轴的摆动为牵连运动,速度为ve。
(3)用速度合成定理,由式(3-2-1)作速度矢量图,如图3-2-8所示。
图中动点的绝对速度va=OAω=rω(a)
图中牵连速度ve=vasinθ(b)
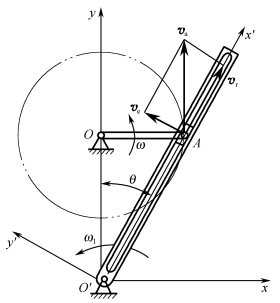
图3-2-8 刨床摆动导杆机构
由图可知sinθ=![]()
将(a)、(c)代入(b)得
![]()
又由ve=ω1O′A得
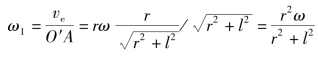
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




