前面研究点的运动和构件的基本运动时,都是以地球作为参考系的。其实,在不同参考系上描述同一物体的运动,会有不同的结论。例如,人站在地面上,看到车厢里的人随列车一起运动,可是坐在列车里的人看到车厢是静止的;在下雨时,对于地面上的观察者来说,雨滴是铅垂向下的,但是对于正在行进的车上的观察者来说,雨滴是倾斜向后的,如图3-2-2所示。为什么同一运动,会出现不同的结果呢?这是因为前者是以地面为参考系,后者是以车厢为参考系。这种不同运动的结果,是因为选择的参考系不同,因而运动结果也不相同。既然同一物体对不同的参考系的运动是不一样的,那么物体对不同的参考系的运动之间有什么关系呢?为此,我们建立合成运动的概念。

桥式起重机
如图3-2-3所示,起重机起吊重物M时,重物既要随小车沿横梁向右运动,又要随卷扬机提升向上运动。显然,重物相对起重机向上运动,相对地面是向右上方运动。把重物M简化为质点,称为动点。把固连于地面的坐标系称为固定参考系,简称定系,用Oxy表示。把相对于地面运动的坐标系(如固连于小车上的坐标系)称为动参考系,简称动系,用O′x′y′表示。
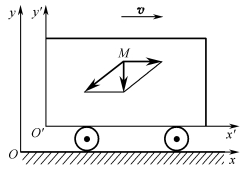
图3-2-2 雨滴的运动
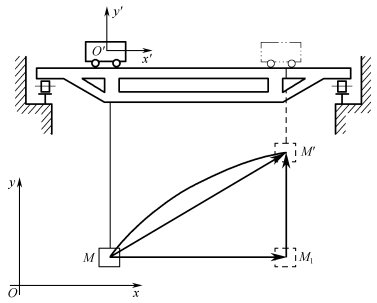
图3-2-3 桥式起重机
为了区别动点对于不同参考系的运动,规定:
绝对运动——动点相对于定系的运动;
相对运动——动点相对于动系的运动;(https://www.xing528.com)
牵连运动——动系相对于定系的运动。
例如,站在河岸观察轮船甲板上走动的旅客,取旅客为动点,河岸为静系,航行的轮船为动系。不同瞬时旅客脚踩轮船甲板上一系列不同的点就是瞬时牵连点,它们在不同瞬时对河岸具有不同的速度,这就是旅客的牵连速度。
图3-2-2中,定系固连于地面上,动系固连于小车上,重物M为动点。重物相对于地面的曲线运动为绝对运动;重物相对于小车的铅垂方向的直线运动为相对运动,小车相对于地面的水平直线运动是牵连运动。从以上三种运动关系可知,动点M相对于地面的绝对运动可分解为动点M相对于小车的相对运动,与小车相对于地面的牵连运动。显然,若没有牵连运动,则动点的相对运动就是它的绝对运动;若没有相对运动,则动点随动系所做的牵连运动就是它的绝对运动。由此可见,动点的绝对运动可看成是动点的相对运动与动点随动系的牵连运动的合成。因此,动点的绝对运动又称为点的合成运动或复合运动。
又如图3-2-4所示中,定系固连于地面上,动系固连于车上,沿直线轨道滚动的车轮上一点为动点。站在地面上的人以地面为定参考系,看其轮缘上点M的运动轨迹是旋轮线,这是绝对运动;而在行驶着的车中的人,以车厢为动参考系看M点,点M相对于车厢的运动是简单的圆周运动,这是相对运动;车厢作为动参考系,车厢相对于地面的运动是简单的平动,这是牵连运动。这样,轮缘上一点的运动就可以看成两个简单运动的合成,即点M相对于车厢做圆周运动,同时车厢相对于地面做平动。
应该指出,动点的绝对运动和相对运动都是指点的运动,它可能做直线运动或曲线运动;而牵连运动则是指参考体的运动,实际上是刚体的运动,它可能做平动、转动或其他较复杂的运动。
选择动点和动系时应注意,动点和动系不能选在同一个构件上,即动点和动系之间必须有相对运动;一般取常接触点为动点,瞬时接触点所在的构件为动系。

沿直线轨道滚动的车轮

图3-2-4 沿直线轨道滚动的车轮
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




