1.自然法
1)运动方程

图3-1-2 点的自然法运动方程
用自然法描述点的运动规律时,按照已知点的运动轨迹,建立自然坐标轴来确定动点的位置。设动点M沿已知轨迹AB运动,如图3-1-2所示,在轨迹上任取一点O为参考原点,在原点两侧分别规定正、负方向。动点在轨迹上的位置,用它到O点的弧长![]() 来决定,
来决定,![]() 为代数值,称为动点M的弧坐标,用符号S表示。动点沿轨迹运动时,其弧坐标S可表示为时间t的单值连续函数,即
为代数值,称为动点M的弧坐标,用符号S表示。动点沿轨迹运动时,其弧坐标S可表示为时间t的单值连续函数,即
![]()
式(3-1-1)称为自然法表示的点的运动方程。
在研究点的运动时,常遇到路程的概念。路程是指动点在某时间间隔内在轨迹上所走过的弧长。路程与弧坐标的概念不同,路程表示动点在某时间间隔内所走过的距离的绝对值,因此它随时间增加而增加,与参考原点位置的选择无关;弧坐标是表示动点某瞬时位置的一个代数值,它与参考原点位置的选择有关。
如图3-1-3所示,若动点M沿轨迹单向运动时,瞬时t1和t2的弧坐标分别为S1和S2,在时间间隔Δt=t2-t1内的路程![]() 与弧坐标S1和S2的关系为
与弧坐标S1和S2的关系为
![]()
即某时间间隔内动点的弧坐标的增量的绝对值等于路程。
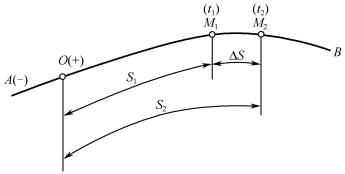
图3-1-3 自然法点的路程
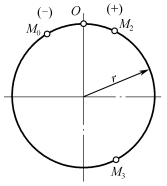
图3-1-4 例3-1-1图
例3-1-1 点M沿半径r=10cm的圆周运动,如图3-1-4所示。其运动方程为S=2t2+5t-3,弧坐标S的单位为cm,时间t的单位为秒(s),试求初瞬时、第1s、第2s及第3s时点的位置,时间间隔0~1s和1~3s内动点走过的路程。
解:由运动方程可知点在每瞬时的位置。将t=0,1,2,3分别代入运动方程S=2t2+5t-3中,可得
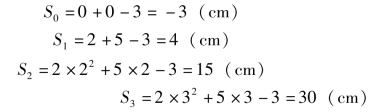
在0~1s和1~3s内动点走过的路程为
![]()
2)速度
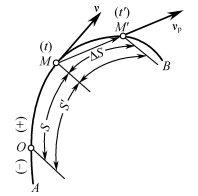
图3-1-5 自然法点的速度
如图3-1-5所示,动点M沿曲线AB运动,瞬时t动点位于M处,其弧坐标为S。在瞬时t′=t+Δt时,动点在M′处,其弧坐标为S′,矢量![]() 是动点在Δt时间内的位移,在Δt时间内动点运动的平均速度为
是动点在Δt时间内的位移,在Δt时间内动点运动的平均速度为
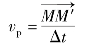
当Δt趋近于零时,M′趋近于M,平均速度趋于某一极限值,该极限值就是动点在位置M处的(瞬时t)的速度,即
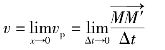
当Δt趋近于零时,线段![]() 趋近于ΔS,所以上式变为
趋近于ΔS,所以上式变为
![]()
速度是矢量,平均速度的方向与位移![]() 的方向相同,瞬时速度v的方向应与位移
的方向相同,瞬时速度v的方向应与位移![]() 趋于零时的极限方向相同,当Δt趋近于零时
趋于零时的极限方向相同,当Δt趋近于零时![]() 的方向为曲线在M点的切线方向,并指向运动的方向。
的方向为曲线在M点的切线方向,并指向运动的方向。
速度的指向,可由![]() 的正负号决定。当
的正负号决定。当![]() 为正值时,点沿轨迹的正向运动,速度指向轨迹的正向;当
为正值时,点沿轨迹的正向运动,速度指向轨迹的正向;当![]() 为负值时,点沿轨迹的负向运动,速度指向轨迹的负向。
为负值时,点沿轨迹的负向运动,速度指向轨迹的负向。
3)加速度

图3-1-6 自然法点的加速度
加速度是表示点运动速度变化快慢的一个重要物理量。在直线运动中,加速度只表示速度大小的变化;在曲线运动中,不仅速度的大小在变化,而且速度的方向也在改变。如图3-1-6所示,在瞬时t和t′,动点M的速度为v和v′,则速度的增量是Δv=v′-v,此速度增量同时包含速度大小与方向的变化,可将它分解为两部分。在矢量![]() 上截取数值等于v的一段OE,连接DE,则Δv分解为Δvn与Δvτ两个分量。Δvn是由于速度v的方向转过vΔφ角所引起的增量;Δvτ则是由于速度v的大小改变所引起的增量,则
上截取数值等于v的一段OE,连接DE,则Δv分解为Δvn与Δvτ两个分量。Δvn是由于速度v的方向转过vΔφ角所引起的增量;Δvτ则是由于速度v的大小改变所引起的增量,则
![]()
将上式除以Δt,并令Δt→0,取各项的极限值,可得加速度为
![]()
上式将加速度分解为两个分量。其中分量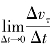 表示速度的大小随时间的变化程度,以aτ表示;分量
表示速度的大小随时间的变化程度,以aτ表示;分量![]() 表示速度的方向随时间的变化程度,以an表示。
表示速度的方向随时间的变化程度,以an表示。
(1)切向加速度aτ。

由上式可得:点的切向加速度其大小等于速度对时间的一阶导数,或弧坐标对时间的二阶导数。
切向加速度的方向是在改点的切线方向,指向由导数正负号绝对:正号表示指向轨迹的正方向;反之指向负方向。v与aτ同号时,点做加速运动,反之v与aτ异号时,则作减速运动。
(2)法向加速度an。
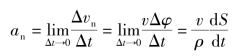
其中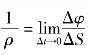 ,表示轨迹在点M处的曲率。因
,表示轨迹在点M处的曲率。因![]() ,所以有
,所以有

于是得:法向加速度an的大小等于速度平方与轨迹在该点的曲率半径之比,方向指向该点的曲率中心。
(3)全加速度a。
因为aτ和an相互垂直,所以全加速度的大小为
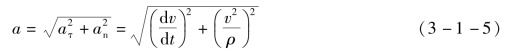
全加速度的方向可用a与切线所夹锐角β来表示

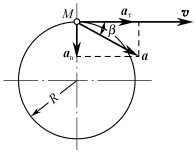
图3-1-7 例3-1-2图
例3-1-2 滚筒加速转动时其轮缘上点的运动方程为S=0.1t3,滚筒半径R=0.5m,如图3-1-7所示。试求5s时点的速度、加速度。
解:(1)速度v。由式(3-1-2)可得
![]()
5s末的速度
![]()
(2)切向加速度aτ。由式(3-1-3)得
![]()
5s末的切向加速度
![]()
(3)法向加速度an。由式(3-1-4)可得
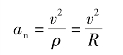
5s末的法向加速度
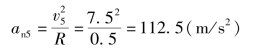
例3-1-3 摇杆滑道机构中的滑块M同时在摇杆OA的滑道中和半径为R的圆弧槽BC中滑动。如图3-1-8所示,摇杆绕O点转动的规律为φ=10t。用自然法求滑块M的运动方程、速度和加速度。已知初始状态时摇杆OA在水平位置。
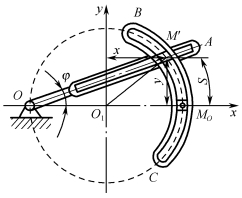
图3-1-8 例3-1-3图
解:(1)求运动方程。选MO为参考原点,逆时针方向为正。滑块M在弧槽内运动,其轨迹可知为以O1点为圆心,O1M为半径的圆弧。则动点M的弧坐标![]()
由几何关系可得(https://www.xing528.com)
![]()
(2)求速度。由式(3-1-2)得
![]()
(3)求加速度。由式(3-1-3)得
由式(3-1-4)得
![]()
由式(3-1-5)得
![]()
由式(3-1-6)得
![]()
2.直角坐标法
1)运动方程
在点的运动的平面内取直角坐标系xOy,动点的位置是由坐标x、y来决定,如图3-1-8所示,建立动点M的坐标x、y随时间t变化的函数关系为
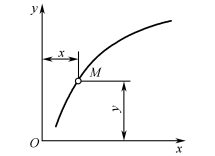
图3-1-9 直角坐标运动方程

式(3-1-7)称为点的直角坐标运动方程,求出任一瞬时动点的坐标值x、y,也就确定了动点在该瞬时的位置。
用坐标法确定动点的运动轨迹时,将不同的t值代入运动方程,求出相应的坐标值,便得到各个瞬时相应的动点位置,连接各点所得到的曲线就是动点的运动轨迹。点的轨迹还可以用下述方程表示,即将坐标方程中的时间t消去,所得到的两个坐标之间的函数关系为

图3-1-10 直角坐标法求位移
![]()
方程(3-1-8)称为动点的轨迹方程。
2)速度
设动点M在平面xOy内运动,其运动方程为
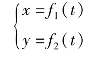
在瞬时t时,点在M处,其坐标为x、y,在瞬时t′=t+Δt时,点在M′处。其坐标为x′、y′,如图3-1-10所示。
由前面可知,点在瞬时t的速度为
![]()
将位移![]() 分别投影在x、y轴上,得到时间Δt内的位移增量Δx、Δy,且Δx=x′-x,Δy=y′-y。
分别投影在x、y轴上,得到时间Δt内的位移增量Δx、Δy,且Δx=x′-x,Δy=y′-y。
点在Δt时间内、x轴方向的平均速度为
![]()
当Δt趋于零时,在x轴上的平均速度的极限值,称为瞬时t动点M在x轴方向的瞬时速度分量,同理可得动点M在y轴方向的瞬时速度分量

由此得速度沿坐标轴的速度分量等于对应坐标对时间的一阶导数。
如图3-1-11所示,若速度沿坐标轴的分量为vx、vy,则速度的大小和方向为

3)加速度
如图3-1-12所示,将加速度a沿x、y轴方向分解为ax、ay,由此得:动点某瞬时的加速度等于x轴方向的加速度分量与y轴方向的加速度分量的矢量和。

全加速度的大小和方向为
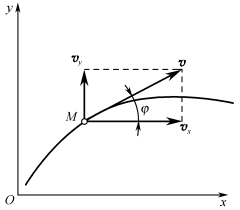
图3-1-11 直角坐标法求速度
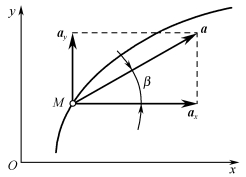
图3-1-12 直角坐标法求加速度
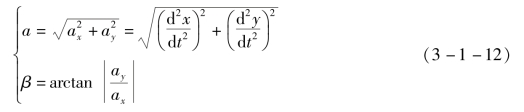
式中 β——a与x轴所夹锐角,a的指向由ax、ay的正负号决定。
例3-1-4 已知动点的直角坐标方程为
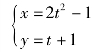
式中,坐标x、y的单位为cm,时间t的单位为s。试求点的运动轨迹,当t=2s时点的位置、速度和加速度。
解:(1)求点的运动轨迹。
![]()
将上式代入x=2t2-1中,得
![]()
将t=2s代入运动方程,可得2s末点的位置

(2)求速度。
2s末动点的速度vx2、vy2为
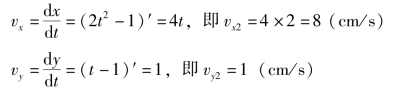
(3)求加速度。
2s末动点的加速度ax2、ay2为

例3-1-5 用直角坐标法求图3-1-8所示滑块M的运动方程、速度和加速度。
解:(1)求运动方程。
选取直角坐标系xO1y,O1点为坐标原点,O1MO方向为x轴,与O1MO垂直方向为y轴,则动点M的坐标方程为
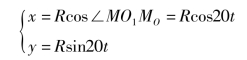
即
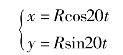
这里指出x2+y2=R2即为坐标法求得动点的轨迹方程。
(2)求速度。
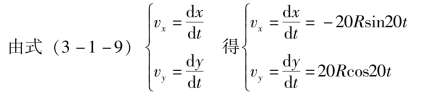
(3)求加速度。
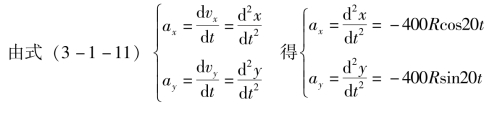
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




