压杆稳定性计算方法

1.压杆稳定的计算

压杆的稳定计算包括：校核稳定性、按稳定性要求确定许可载荷和选择截面三方面。采用的方法有安全系数法和折减系数法两种。

1）安全系数法

为保证压杆的稳定性，压杆的稳定性条件为

或

式中　FP——压杆的工作压力；

　　　Pcr——压杆的临界力；

　　　nw——压杆的工作稳定安全系数；

　　　[nw]——规定的稳定安全系数。

考虑到压杆存在初曲率和载荷偏心等不利因素，规定的稳定安全系数[nw]比强度安全系数要大。通常在常温、静载荷下，钢材的[nw]为1.8～3.0；铸铁的[nw]为4.5～5.5；木材的[nw]为2.5～3.5。

当压杆的横截面有局部削弱（如开孔、刻槽等）时，应按削弱后的净面积进行强度校核。但作稳定计算时，可不考虑截面局部削弱后的影响。

按式（2-6-12）或式（2-6-13）进行稳定计算的方法，称为安全系数法。其解题步骤如下：

（1）根据压杆的尺寸和约束条件，分别计算其在各个弯曲平面弯曲时的柔度λ，从而得到最大柔度λmax；

（2）根据最大柔度λmax，选用计算临界应力的公式，然后算出σcr和Pcr；

（3）利用式（2-6-13）或式（2-6-14）进行稳定校核或求许可载荷。

2）折减系数法

将式（2-6-12）两边同除以压杆的横截面面积，得

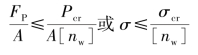
令

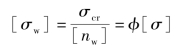
即

式中　[σw]——稳定许用应力。

这里将稳定许用应力表示成强度许用应力[σ]乘以一个折减系数φ。由于临界应力σcr和稳定安全系数[nw]均随压杆的柔度λ而变化，则[σw]也因λ而异，故φ是λ的函数。几种材料对应于不同λ的φ值见表2-6-3。

表2-6-3　压杆的折减系数φ

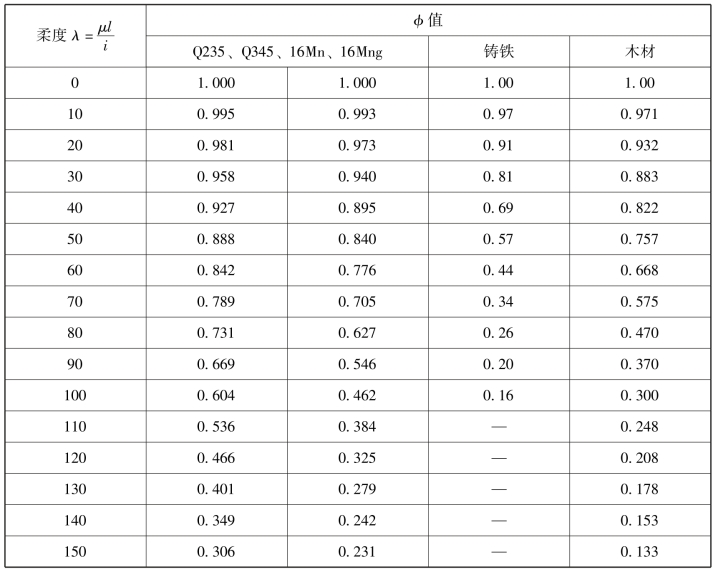
引入折减系数后，压杆的稳定条件可写成

按式（2-6-14）进行稳定计算的方法称为折减系数法。在按稳定条件选择压杆截面尺寸时，用此法比较方便。

例2-6-3　一工字钢柱上端自由，下端固定，如图2-6-4所示。已知l＝4.2×103mm，FP＝280kN，材料为Q235钢，[σ]＝160MPa。试按稳定条件选择工字钢型号。

解：据稳定条件式（2-6-14），压杆的截面面积应为

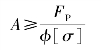
由于式中的φ值又与截面面积尺寸有关，故不能直接求得A值。为此，需先设定一φ值，进行试算。

（1）第一次试算。第一次试算时一般取其中间值φ1＝0.5，由式（2-6-14）得

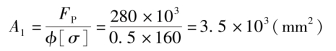
查本书后的附录，初选20a号工字钢，其截面面积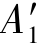＝3.55×103mm2，最小惯性半径imin＝iy＝21.2mm。

对于初选的20a号工字钢，应校核其是否满足稳定条件。压杆柔度

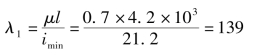
查表2-6-3得折减系数（按直线插值法求得）为＝0.354。

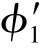与φ1相差过大，需进行稳定性校核。由稳定条件，有

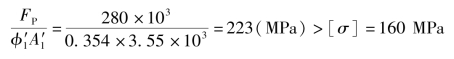
说明初选的20a号工字钢不能满足稳定性要求，需重选。

（2）第二次试算。

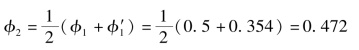
由稳定条件得

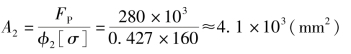
查本书后的附录，重选22a号工字钢，其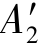＝4.2×103mm2，imin＝iy＝23.1mm。此时压杆的柔度为

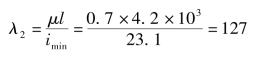
再进行稳定校核，有(www.xing528.com)

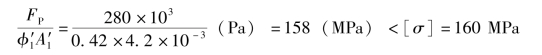
即满足稳定条件，故最后选用22a号工字钢。应注意，若压杆截面有局部削弱时，尚须进行强度校核。

2.提高压杆稳定性的措施

1）合理选择材料

对于细长杆，临界应力，σcr与压杆材料的E成正比。故选用弹性模量较大的材料，可提高压杆的稳定性。但应注意一般钢材的弹性模量E大致相同，故选用高强度钢并不能起到提高其稳定性的作用。

对于中长杆，由临界应力的经验公式可知，材料屈服点或强度极限的增长，可引起临界应力的增长，故选用高强度材料能提高其稳定性。

对于短粗杆，选用高强度材料当然可提高其承载能力。

2）改善杆端支承情况

不同的杆端约束影响长度系数μ，杆端约束的刚性越强，μ值越小，则柔度就越小，稳定性就越高。因此，加强杆端约束的刚性，可提高压杆的稳定性。

3）减小压杆的长度

减小压杆长度，可提高压杆的柔度，提高其稳定性，所以尽量减小压杆长度和在压杆中间增加支座或支承，可提高压杆稳定性。

4）选择合理的截面形状

由欧拉公式知，截面的惯性矩I越大，临界力越大，稳定性越好。因此，使材料尽量远离中心轴，可使柔度减小，稳定性提高。

【任务实施】

某机器连杆如图2-6-1所示，截面为工字形，其Iy＝1.42×104mm4，Iz＝7.42×104mm4，A＝552mm2。材料为Q275钢，连杆所受的最大轴向压力FP＝30kN，取规定的稳定安全系数[nw]＝4。试校核压杆的稳定性。

解：连杆失稳时，可能在x-y平面发生弯曲，这时两端可视为铰支；也可能在x-z平面发生弯曲，这时两端可视为固定。此外，在上述平面内弯曲时，连杆的有效长度和惯性矩也不同。故应先计算出这两个弯曲平面内柔度λ，以确定失稳平面，再进行稳定校核。

（1）柔度计算。在x-y平面内失稳时，截面以z为中性轴，柔度

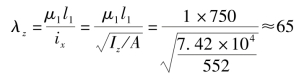
在x-z平面内失稳时，截面以y为中性轴，柔度

因λz＞λy，表明连杆在x-y平面内稳定性较差，故只需校核连杆在此平面内的稳定性。

（2）稳定性校核。

工作压力：FP＝30kN

临界力：由于λz＝65＜λc＝96，属中长杆，需用经验公式。现按抛物线公式算得临界应力为

则临界力为

代入式（12-14），得

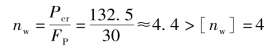
故连杆的稳定性足够。

【任务小结】

1.稳定性的概念

（1）不稳定平衡状态：受到扰动不能够自行恢复的平衡状态。

（2）稳定平衡状态：受到扰动能够自行恢复的平衡状态。

（3）压杆的稳定性：压杆维持直线平衡状态的能力。

2.压杆的临界应力

（1）当λ≥λp（λc）时，属于细长杆（大柔度杆），用欧拉公式计算，即

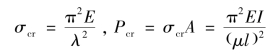
（2）当λ0≤λ≤λp（λc）时，属于中长杆（中柔度杆），用经验公式计算，即

（3）当λ＜λs时，属于短粗杆（小柔度杆），用轴向压缩公式计算，即

3.稳定性计算

压杆的稳定性条件：

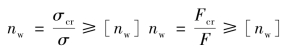
4.提高压杆稳定性的措施

（1）选择合理的截面形状；

（2）减小杆长，改善两端支承；

（3）合理选择材料。

【实践训练】