欧拉公式及其适用范围

1.细长压杆的临界力

一个压杆的临界力，既与杆件本身的几何尺寸有关，又与杆端的约束条件有关。

1）两端铰支压杆的临界力

取一两端铰支细长杆，受轴向压力P作用。当P＝Pcr时，稍干扰后，压杆可在微弯状态下保持平衡，如图2-6-4（a）所示。因此，在这种状态下求得的轴向压力就是临界力。

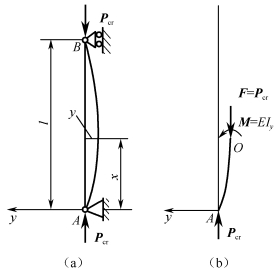
图2-6-4　两端铰支压杆的临界力

若压杆在微弯状态下平衡时，横截面上的应力在弹性范围之内，通过理论推导得临界力的计算公式为

式中　I——杆横截面对中性轴的惯性矩；

　　　E——弹性模量；

　　　l——杆的长度。

式（2-6-1）是由欧拉（L.Euler）先导出的，所以通常称为欧拉公式。应用欧拉公式应注意两点：一是本公式只适用于弹性稳定问题；二是公式中的I为压杆失稳弯曲时截面对其中性轴的惯性矩，当截面对不同主轴的惯性矩不等时，应取其最小值。

2）杆端约束对临界力的影响

杆端支承对杆件变形起约束作用，不同形式的支承对杆件的约束作用也不同。因此，同一压杆在两端约束不同时，其临界力值也必然不同。对于表12-1中给出的杆端约束不同的几种压杆，按照上述推导方法，可求出其临界力的计算公式，并写成下列统一形式

式（2-6-2）为欧拉公式的普遍形式，式中μ是与支承情况有关的长度系数，其值见表2-6-1。

表2-6-1　压杆的长度系数μ

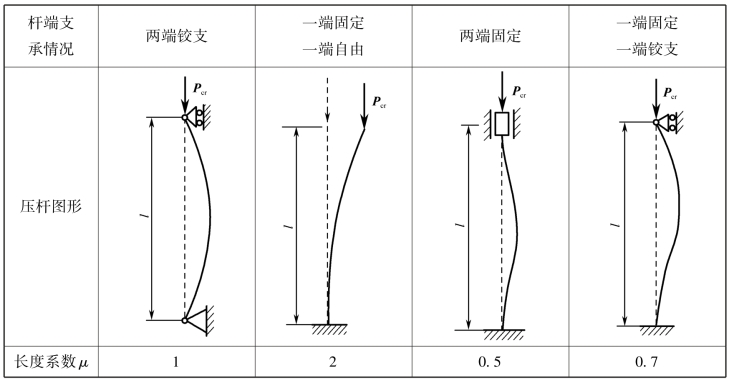
表2-6-1中列出的杆端约束，都是典型的理想约束。但在工程实际中，杆端约束情况复杂，有时很难简单地归结为哪一种理想约束。这时应根据实际情况具体分析，参考设计规范确定μ值。

例2-6-1　图2-6-5所示压杆由14号工字钢制成，其上端自由，下端固定。已知钢材的弹性模量E＝210GPa，屈服点σs＝240MPa，杆长l＝3×103mm。试求该杆的临界力Pcr和屈服载荷Fs。

解：（1）计算临界力。对14号工字钢，查本书后的附录得

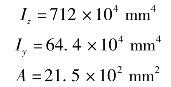
压杆应在刚度较小的平面内失稳，故取Imin＝Iy＝64.4×104mm4。由表12-1查得μ＝2。将有关数据代入式（2-6-2）即得该杆的临界力

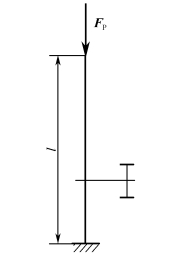
图2-6-5　例2-6-1图

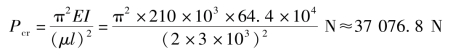
（2）计算屈服载荷。

（3）讨论。

Pcr∶Fs＝37076.8∶516000≈1∶13.9，即屈服载荷是临界力的近14倍。可见细长压杆的失效形式主要是稳定性不够，而不是强度不够。

2.压杆的临界应力

1）细长压杆的临界应力

当压杆处于临界状态时，临界力作用下横截面上的平均正应力称为临界应力，用σcr表示，即

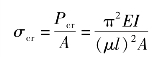
由截面图形的几何性质可知，，其代入上式得

则得细长压杆临界应力公式

式中，称为压杆的柔度，是一个量纲为1的量。由式（2-6-3）可见，λ越大，即杆越细长，则临界应力越小，压杆越容易失稳；反之，λ越小，压杆就越不易失稳。

2）欧拉公式的适用范围

式（2-6-3）实质上是欧拉公式的另一种表达形式。前述及欧拉公式只适用于弹性范围，由此可得欧拉公式的适用条件为

将上式改写成

再令

得

式（2-6-5）表明只有当压杆的实际柔度λ大于或等于限值λp时，才能用欧拉公式计算其临界应力和临界力。

压杆的实际柔度随压杆的几何形状尺寸和杆端约束条件的不同而变化，但是λp仅由材料性质确定。不同材料的λp可按式（2-6-4）计算。如Q235钢，取E＝206 GPa，σp＝200MPa，代入式（2-6-4）得

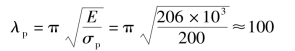
即由Q235钢制成的压杆，只有当λ≥100时，欧拉公式才适用。(www.xing528.com)

工程上把λ≥λp的压杆称为细长压杆，或大柔度杆。

3）中长压杆的临界应力经验公式

当压杆的λ＜λp，但大于某一界限值λ0时，称为中长杆或中柔度杆，其主要失效形式是失稳问题，如内燃机连杆、千斤顶丝杆等。对于中长杆，其临界应力已超出比例极限，欧拉公式不再适用。这类压杆的临界力一般根据经验公式确定。经验公式为直线型和抛物线型两类。

（1）直线公式。

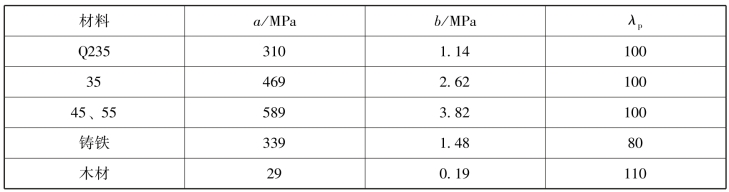
式中，a、b为与材料性质有关的常数。一般常用材料的a、b和λp值见表2-6-2。

表2-6-2　直线公式的系数a、b和λp值

直线公式（2-6-6）也有其适用范围，即压杆的临界力不能超过材料的极限应力σ0（σs或σb），即

对于塑性材料，

式中，λs是塑性材料压杆使用直线公式时柔度λ的最小值。

对于脆性材料，将式（2-6-7）中的σs换成σb确定相应的λb。将λs和λb统一记为λ0，则直线公式适用范围的柔度表达式为

如Q235钢，其σs＝235MPa，a＝310MPa，b＝1.14MPa代入式（2-6-7）得

即由Q235钢制成的压杆，当其柔度66≤λ＜100时，才可以使用直线公式。

当压杆柔度λ＜λ0时，称为短粗杆或小柔度杆。其失效形式是强度不足。故其临界应力就是屈服点或抗拉强度，即σcr＝σs（或σb）。

（2）抛物线公式。

式中　σ0——材料的极限应力；

　　　k——与材料有关的常数；

　　　λ——压杆的实际柔度。

在我国的钢结构设计规范中，对塑性中长压杆提出如下抛物线型经验公式

对于普通碳素钢，式中的系数α为0.43，于是由式（2-6-8）和式（2-6-9）得

式中，λc为欧拉曲线与抛物线连接点处的柔度值（见图2-6-6），即根据抛物线公式确定的应用欧拉公式（2-6-3）时压杆柔度的最小值。当λ＝λc时，式（2-6-3）与式（2-3-9）应相等，于是可得λc的计算式

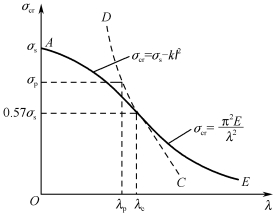
图2-6-6　欧拉曲线

如Q235钢，其E＝206GPa，σs＝235MPa，代入式（2-6-11）得

这表明由Q235钢制压杆，应以λ＝123作为使用欧拉公式和抛物线公式的分界点。这与上个问题中以λp＝100作为其分界点不一致。但由于工程实际中的压杆，不可能处于理想的轴向受压，材料性质也不均匀，而经验公式是根据试验资料得来的，更能反映实际情况。

由式（2-6-8）可知，当λ＝0时，σcr＝σ0。即从理论上讲，抛物线公式的适用范围是0≤λ≤λc。但在实际应用中，当λ很小时，压杆的失效形式是破坏而非失稳，故只需进行强度计算。

压杆材料的性质不同，式（2-6-8）中的λ和k也不同。下面给出几种常见材料的抛物线公式及其适用范围：

两类经验公式中，直线公式较简单，提出较早；抛物线公式是近代的实验研究成果。在工程设计中，两者可通用，但对铸铁、铝合金和木材多用前者，对结构钢多用后者。

综上所述，压杆可据其柔度分为三类，用不同的公式计算其临界应力和临界力，压杆的临界应力随柔度的增大而减小，表明压杆越细长，越易于失稳。

（1）当λ≥λp（λc）时，属于细长杆（大柔度杆），用欧拉公式计算，即

（2）当λ0≤λ≤λp（λc）时，属于中长杆（中柔度杆），用经验公式计算，即

（3）当λ＜λs时，属于短粗杆（小柔度杆），用轴向压缩公式计算，即

例2-6-2　3个圆截面压杆，材料为钢Q235，E＝206GPa，σp＝200MPa，σs＝235 MPa，直径d均为160mm，各杆两端均为铰支，长度分别为l1＝5×103mm，l2＝2.5×103mm，l3＝1.25×103mm。试计算各杆的临界力。

解：（1）有关数据。

（2）计算各杆的临界力。