拉伸压缩与弯曲组合变形优化方案

1.拉伸（压缩）与弯曲组合变形的概念

在工程中许多构件在外力作用下，往往包含两种或两种以上的基本变形，称为组合变形。

通过对工程实例的简单分析，可以看出这些构件在外力作用下均同时产生两种或两种以上的变形，其中又以弯曲与拉伸（压缩）组合变形、弯曲与扭转组合变形最为普遍。

在材料服从胡克定律及小变形的前提下，构件虽然同时发生几种基本变形，但其中任一种基本变形都不会改变其他另一种基本变形所引起的应力和应变，即每一种基本变形都是各自独立、互不影响的。于是可以分别计算每一种基本变形各自引起的应力和变形，然后求出这些应力和变形的总和，即为构件在原载荷作用下的应力和变形。这就是叠加原理。从而进一步就可以确定出构件在危险点处的应力，并进行强度计算。

2.拉伸（压缩）与弯曲组合变形的强度计算

图2-5-2（a）所示为一个左端固定而右端自由的矩形截面杆，在其自由端作用集中力F，它位于杆的纵向对称面内，并与杆的轴线成夹角α，现以此为例说明杆在拉伸（压缩）与弯曲组合变形时的强度计算问题。

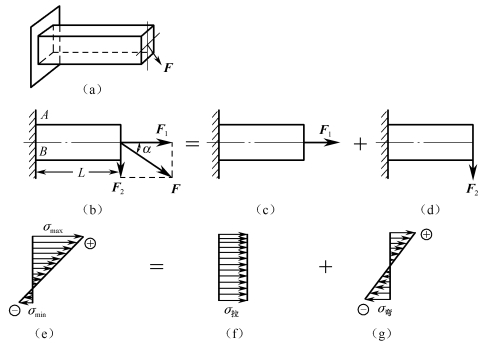
图2-5-2　拉伸与弯曲组合变形

如图2-5-2（b）所示，将力F沿杆的轴线和轴线的垂线方向分解为两个分力F1和F2，其值为

在轴向拉力F1作用下，杆产生拉伸变形。其各横截面上都有相同的轴力FN＝F1，且拉伸正应力是均匀分布的，见图2-5-2（f），其值为

在横向力F2作用下，杆产生弯曲变形。其固定端的横截面上弯矩最大，即Mmax＝F2L。在固定端横截面的上下边缘的弯曲正应力绝对值最大，如图2-5-2（g）所示，其值为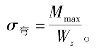

按叠加原理，作出图2-5-2（e）中（当σ拉＜σ弯时）固定端横截面上的总正应力分布图。上、下边缘A、B处的正应力按代数值分别称为σmax、σmin，即

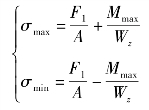
由上述可见，固定端横截面是危险截面，其上边缘各点是危险点。由于叠加后所得的应力状态仍然是单向应力状态，因此它的强度条件为

如果F不是拉力而是压力，则固定端横截面上A、B处的应力为

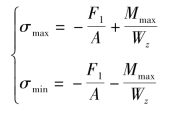
此时，固定端横截面的下边缘各点是危险点，其危险点处的正应力为压应力，因此它的强度条件为(www.xing528.com)

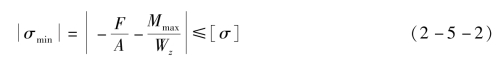
对于截面形状对中性轴不对称，或者杆件材料的拉伸与压缩许用应力不相同的情形，则需另行讨论。应当注意，虽然以上讨论为杆件一端固定一端自由的情况，但其原理同样适用于其他支座和载荷情况下杆的拉伸（压缩）与弯曲组合变形。

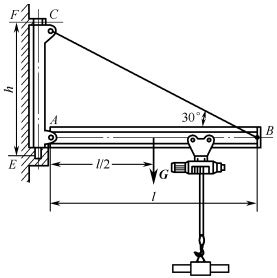
图2-5-3　简易起重机工程实例

例2-5-1　简易起重机如图2-5-3所示，最大起重量G＝11kN，横梁AB为工字钢，许用应力[σ]＝170MPa，梁自重不计，按拉伸弯曲组合变形准则选择工字钢的型号。

解：（1）横梁的变形分析。如图2-5-4（a）所示，将拉杆BC的对横梁的作用力FB分解为FBx、FBy，将A点的固定铰链的约束力分解为FAx、FAy，力FAx和FBx使横梁AB发生轴向压缩变形；力G、FAy和FBy使梁发生弯曲变形，梁AB发生压缩、弯曲组合变形，且电葫芦在中点时为最危险状态。

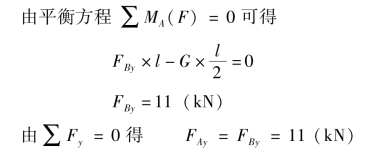
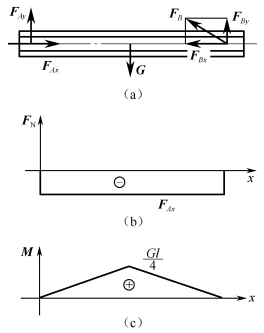
图2-5-4　例2-5-1图

由图11-1得　FBx＝FBycotα＝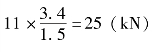

由∑Fx＝0得　FBx＝FAx＝11（kN）

（2）横梁内力分析。画梁AB的轴力图[见图2-5-4（b）]、弯矩图[见图2-5-4（c）]。

横梁截面的轴向压力为　FN＝FAx＝25（kN）

横梁截面中点的最大弯矩＝18.7（kN·m）

（3）选择工字钢型号。查本书后的附录，初选16号工字钢Wz＝141cm3＝141×103mm3，A＝26.1cm2＝26.1×102cm2

由强度准则可知

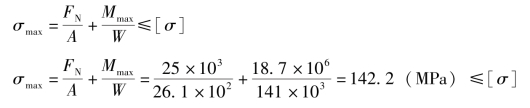
所以选择16号工字钢强度足够。