一般情况下，梁横截面上的剪力和弯矩是随梁横截面位置的变化而连续变化的，把剪力和弯矩可表示为截面坐标x的函数
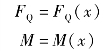
以上两式称为梁的剪力方程和弯矩方程。
2.剪力图和弯矩图
与绘制轴力图和转矩图一样，也可以绘制梁各横截面上的剪力FQ和弯矩M随梁横截面位置参数x变化的曲线，分别称为梁的剪力图和弯矩图。
例2-4-2 简支梁如图2-4-11所示，在C处作用一集中力F，列出此梁的剪力方程和弯矩方程，并画剪力图和弯矩图。
图2-4-11 例2-4-2图
解：（1）求支座反力。由平衡方程得
（2）列梁的剪力方程和弯矩方程。以梁的左端A点为坐标原点。由于集中力F作用在C点，梁在AC和CB段内的剪力和弯矩不能用同一方程来表示，应分段考虑。在AC段内取距梁左端A点为x1的任意截面，以x1截面左侧梁确定该截面上的剪力方程和弯矩方程分别为
同理，在CB段内取距梁左端A点为x2的任意截面，以x2截面左侧梁确定该截面上的剪力方程和弯矩方程分别为
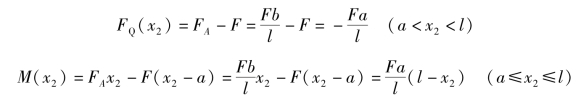
（3）画剪力图。由剪力方程知，剪力图为分段的水平线，如图2-4-11（b）所示。
（4）画弯矩图。由弯矩方程知，弯矩图为分段的斜直线，如图2-4-11（c）所示。
AC段：当x1＝0时，M1＝0；当x1＝a时，
CB段：当x2＝a时，
；当x2＝l时，M2＝0。
据以上数据可画出弯矩图[见图2-4-11（c）]。由图可见，在集中力作用处（C截面），其左、右两侧横截面上弯矩相同，Mmax＝
，而剪力图沿力的方向发生突变，突变幅值等于集中力F的大小。
例2-4-3 简支梁如图2-4-12所示，在C点作用一集中力偶MO，列出此梁的剪力方程和弯矩方程，画剪力图和弯矩图。
图2-4-12 例2-4-3图
解：（1）求支座反力。由平衡方程得
（2）列梁的剪力方程和弯矩方程。以梁的左端A点为坐标原点。由于集中力偶MO作用在C点，将梁分为AC和CB两段，分别在两段内取截面x1，x2，根据截面左侧梁上的外力列出剪力方程和弯矩方程。
AC段：
（3）画剪力图。整个梁上各截面剪力均为
，故剪力图为水平线，如图2-4-12（b）所示。(www.xing528.com)
（4）画弯矩图。
AC段：当x1＝0时，M1＝0；当x1→a时，即在C点稍左的截面处，M1＝-
CB段：当x2→a时，即在C点稍右的截面处，
；当x2＝l时，M2＝0。
据以上数据可画出弯矩图[见图2-4-12（c）]。由图可见，在C截面处弯矩图发生突变，突变幅值为MO。
例2-4-4 简支梁如图2-4-13所示，作用均布载荷q，列出梁的剪力方程和弯矩方程，画剪力图和弯矩图。
图2-4-13 例2-4-4图
解：（1）求支座反力。由平衡方程得
（2）列剪力方程和弯矩方程为
（3）画剪力图。由剪力方程知，剪力图为斜直线。确定直线的两个端点：当x→0时，
；当x→l时，
，即可画出剪力图[见图2-4-13（b）]。
（4）画弯矩图。由弯矩方程知，弯矩图为抛物线，要绘出此曲线至少需要确定三个点：x＝0，M＝0；x＝l/2，M＝ql2/8；x＝l，M＝0。由此可画出弯矩图[见图2-4-13（c）]。
由图可见，在两支座内侧横截面上剪力的绝对值最大，其值为
；在梁中点横截面上，剪力FQ＝0，弯矩最大，其值为
3.弯矩、剪力和载荷集度间的微分关系
梁上的弯矩、剪力和载荷集度间存在着普遍的规律（证明从略）：弯矩方程的一阶导数等于剪力方程，而剪力方程的一阶导数等于载荷集度，即
利用这些微分关系可以对梁的剪力图、弯矩图进行绘制和检查，由导数的性质可知：
（1）无分布载荷作用的梁段上，即q（x）＝0，由式（b）知，FQ（x）＝常数，即此段梁截面上的剪力为一常数，剪力图为水平线；再由式（a）知，M（x）为x的线性函数，即弯矩图为斜直线，且直线的斜率为FQ（x）＝常数。
（2）有均布载荷作用的梁段上，若均布载荷方向向下，q（x）＝-q，由式（b）知，FQ（x）为x的线性函数，剪力图为斜直线，且直线的斜率为负；再由式（a）可知M（x）为x的二次函数，即弯矩图为抛物线（凹向向下）。若均布载荷方向向上，q（x）＝＋q，FQ（x）为斜直线，且直线的斜率为正，M（x）为抛物线（凹向向上），且在剪力等于零的截面，弯矩有极值。
（3）在集中力作用处，剪力图沿力的方向发生突变，突变幅度等于集中力的大小，弯矩图有折点。
（4）在集中力偶作用处，剪力图没有变化，弯矩图发生突变，突变的幅度等于集中力偶的大小，集中力偶顺时针转向时，弯矩图向上突变，否则，弯矩图向下突变。
例2-4-5 如图2-4-14所示，外伸梁AD上作用有均布载荷q，集中力偶MO＝3qa2/2，集中力F＝qa/2，用简便方法画出该梁的剪力图和弯矩图。
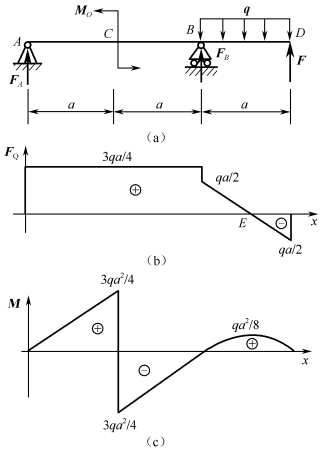
图2-4-14 例2-4-5图
解：（1）求支座反力。由平衡方程得
集中力、集中力偶及均布载荷的始末端将梁分为AC、CB、BD三段。
（2）画剪力图。从梁的左端开始，A点处有集中力，剪力图沿力方向向上突变FA＝3qa/4；AC段无载荷作用，剪力值保持为常量；C点处作用有集中力偶，剪力值不受影响；B点处有集中力，剪力图沿力实际方向向下突变FB＝qa/4；BD段有均布载荷q作用，剪力图为斜直线，B点右侧临界截面（记作B＋）的剪力FQB＋＝qa/2，D点左侧临近截面（记作D-）的剪力FQD-＝-qa/2，此两点连线即BD段的剪力图；D点有集中力F＝qa/2，剪力图沿力的方向向上发生突变qa/2回到坐标轴。由此得到图2-4-14（b）所示的剪力图。
（3）画弯矩图。从梁的左端开始，AC段无载荷作用，弯矩图为斜直线，确定A＋、C-两截面的弯矩值分别为MA＋＝0、MC-＝3qa2/4，此两点连线即AC段的弯矩图；C点处有逆时针旋转的力偶，弯矩图向下突变MO＝3qa2/2，则MC＋＝3qa2/4-3qa2/2＝-3qa2/4；CB段无载荷作用，弯矩图为斜直线，确定C＋、B-两截面的弯矩值分别为MC＋＝-3qa2/4、MB-＝0，此两点连线即CB段的弯矩图；B点处有集中力FB，弯矩图出现转折；BD段有均布载荷q作用，弯矩图为抛物线，其凹向与均布载荷同向向下，确定B＋、E、D-各截面的弯矩值分别为MB＋＝0、ME＝qa/2×a/2-qa/2×a/4＝qa2/8、MD-＝0，通过这三点的弯矩值画出抛物线，即得图2-4-14（c）所示的弯矩图。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
