轴向拉伸或轴向压缩变形是杆件基本变形之一。轴向拉伸或压缩变形的受力及变形特点是,杆件受一对大小相等、方向相反、作用线沿杆件轴线方向的力的作用,杆件伸长或缩短,称为拉伸或压缩。我们把发生轴向拉伸(压缩)的杆件简称为拉(压)杆。轴向拉伸或压缩的杆件的端部可以有各种连接方式,如果不考虑其端部的具体连接情况,其计算简图均可简化为图2-1-5所示结构。

图2-1-5 轴向拉伸和压缩的概念
1.轴力
根据内力的概念,我们知道内力可能沿任何方向作用,但如果内力沿着构件的轴线方向,我们就把这个内力称为轴力,用FN表示。区别于轴向力,轴向力是构件所受的外力,此外力沿着轴线方向;但轴力是构件内部的力,即内力。
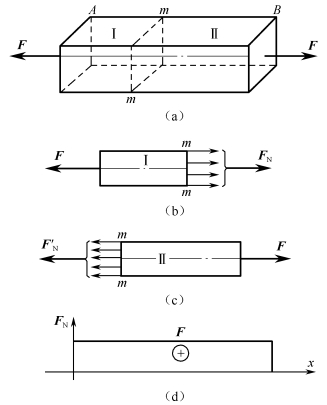
图2-1-6 拉(压)杆横截面上的内力
图2-1-6(a)所示为一受拉杆件的力学模型,为了确定其横截面的轴力,沿截面m—m把杆件截开,分为左、右两段,取其中任意一段为研究对象。杆件在外力作用下处于平衡,则左、右两段也必然处于平衡。左段上有力F和截面内力作用[见图2-1-6(b)],由二力平衡条件,该内力必与外力F共线,且沿杆件的轴线方向,则为轴力FN。由平衡方程可求出轴力的大小为

同理,右段上也有外力F和截面内力 ,[见图2-1-6(c)],满足平衡方程。因FN与
,[见图2-1-6(c)],满足平衡方程。因FN与 是一对作用力与反作用力,必等值、反向和共线。因此取左段求出的轴力FN,还是取右段求出的内力
是一对作用力与反作用力,必等值、反向和共线。因此取左段求出的轴力FN,还是取右段求出的内力 ,都表示m—m截面的内力。拉杆的轴力正负规定为:背离截面方向的轴力为正,指向截面的轴力为负。
,都表示m—m截面的内力。拉杆的轴力正负规定为:背离截面方向的轴力为正,指向截面的轴力为负。
2.轴力图
为了形象地表明各截面轴力的变化情况,以杆的端点为坐标原点,取平行杆轴线的坐标轴为横坐标x轴,称为基线,其值代表截面位置,取FN轴为纵坐标轴,其值代表对应截面的轴力值。正值绘在基线上方,负值绘在基线下方,绘制轴力随截面x变化的曲线图称为轴力图,如图2-1-6(d)所示。
例2-1-1 杆件受力如图2-1-7所示,画出该杆件的轴力图。
解:(1)内力分析。在AB段任取截面m—m假想将杆截开,设取左段为研究对象[见图2-1-7(b)],假定该截面上的轴力为FN1,且为正。由平衡方程
![]()
得
![]()
负号表示FN1的实际方向与所设的方向相反,截面受压。
同理,在BC段任取截面n—n假想将杆截开,设取左段为研究对象[见图2-1-7(d)],以FN2代表该截面上的轴力,且为正。由平衡方程
![]()
得
![]()
(2)绘制轴力图。杆AB间所有截面的轴力都相等,都等于FN1,FN1为负,所以AB之间的轴力图为一在基线下方的水平直线;杆BC间所有截面的轴力都相等,都等于FN2且为正,所以BC之间的轴力图为一在基线上方的水平直线,如图2-1-7(c)所示。
由上例可知,杆件任一截面的轴力FN(x),等于截面一侧左段(或右段)杆件上轴向外力的代数和。左段向左(或右段向右)的外力产生正轴力,反之产生负轴力。
例2-1-2 一杆及其受力情况如图2-1-8(a)所示,F1=16kN,F2=10kN,F3=20kN,作杆的轴力图。
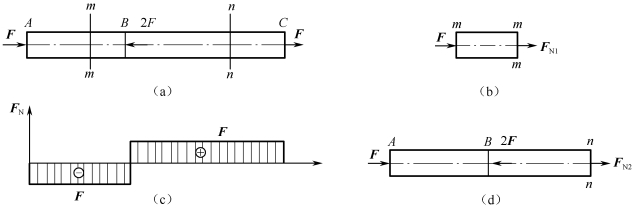
图2-1-7 例2-1-1图
解:(1)求约束反力。
由平衡方程FD-F3-F2+F1=0,得FD-20kN-10kN+16kN=0,求得FD=14kN
(2)内力分析。
求AB段轴力,假想在AB段任一截面1—1处截断,取右段[见图2-1-8(b)],并设轴力FN1为正。由平衡方程得
![]()
结果为正,故FN1为拉力。
求BC段轴力,假想在BC段任一截面2—2处截断,取右段[见图2-1-8(c)],设轴力FN2为正。由平衡方程得
![]()
结果为正,故FN2为拉力。
若取左段[见图2-1-8(d)],设轴力FN2为正。由平衡方程得
![]()
结果与取右段相同。
求CD段轴力,假想在CD段任一截面3—3处截断,取左段[见图2-1-8(d)],并设轴力FN3为正。由平衡方程得
![]()
结果为负值,故FN3为压力。(https://www.xing528.com)
(3)作轴力图。AB段轴力16kN,轴力图为在基线上方的水平直线;BC段轴力为6kN,轴力图为在基线上方的水平直线;CD段轴力为-14kN,轴力图为在基线下方的水平直线。
3.拉(压)杆的应力
同种材料制成粗细不同的两根直杆,在相同轴向拉力的作用下,杆内的轴力相同。随着拉力增大,细杆将首先被拉断。这说明只凭内力不能判断构件的强度,杆件的强度不仅取决于内力的大小,而且与截面面积的大小有关,即构件的强度取决于内力在截面上分布的密集程度。为此引入应力的概念。内力在截面上的集度称为应力,垂直于截面的应力称为正应力,平行于截面的应力称为切应力。
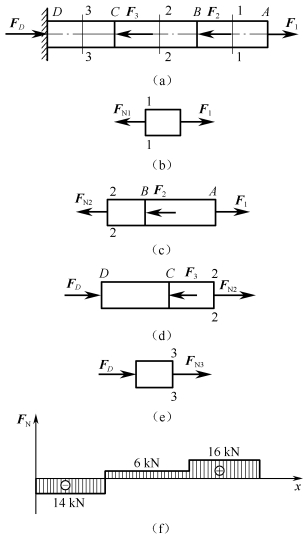
图2-1-8 例2-1-2图

图2-1-9 拉(压)杆横截面上的应力
4.拉(压)杆横截面上的应力
图2-1-9(a)所示为一等截面直杆,假定在未受力前在该杆侧面作相邻的两条横向线ab和cd,然后使杆受拉力F作用发生变形,如图2-1-9(b)所示,并可观察到两横向线平移到a′b′和c′d′的位置且仍垂直于轴线。这说明,杆件的任一横截面上各点的变形是相同的,即变形前是平面的横截面,变形后仍保持为平面且仍垂直于杆的轴线,称为平面假设。根据这一假设,横截面上所有各点受力相同,内力均匀分布,方向垂直于横截面,如图2-1-9(c)所示。
![]()
式中,FN为轴力;A为杆的横截面面积。由式(7-1)知,正应力的正负号取决于轴力的正负号,若FN为拉力,则σ为拉应力;若FN为压力,则σ为压应力,并规定拉应力为正,压应力为负。
5.拉(压)杆的强度计算
为保证拉(压)杆在外力作用下能够安全、可靠地工作,必须使构件横截面的应力小于或等于构件材料的许用应力。当构件各截面的应力不等时,应使构件截面上的最大工作应力小于或等于材料的许用应力。这一条件称为强度设计准则,即

式中,[σ]为许用应力。应用式(7-2)可以解决以下三类计算问题。
(1)校核强度。已知作用外力F、横截面积A和许用应力[σ],计算出最大工作应力,验算是否满足强度准则,从而判断构件是否能够安全、可靠地工作。
(2)设计截面尺寸。已知作用外力F、许用应力[σ],由强度准则计算出截面面积A,即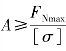 ,然后根据要求的截面形状,设计出构件的截面尺寸。
,然后根据要求的截面形状,设计出构件的截面尺寸。
(3)确定许可载荷。已知构件的截面面积A、许用应力[σ],由强度准则计算出构件所能承受的最大内力FNmax,即9FNmax≤[σ]A,再根据内力与外力的关系,确定出杆件允许的最大载荷F。

离合器踏板
例2-1-3 汽车离合器踏板如图2-1-10所示,已知踏板所受压力为FQ=400N,拉杆1的直径D=9mm,杠杆臂长L=330mm,l=56mm,拉杆的许用应力[σ]=50MPa。试校核拉杆1的强度。
解:(1)计算拉杆1上的拉力FP。

图2-1-10 例2-1-3图
由平衡方程∑MO(F)=0 可得 FQL-FPl=0
![]()
(2)校核拉杆1的强度。
拉杆1两端受到FP=2357N的拉力作用发生拉伸变形,拉杆1中间各截面的轴力FN=FP=2357N,由强度条件可知
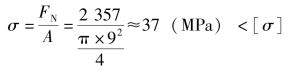
故拉杆1的强度足够。

图2-1-11 例2-1-4图
例2-1-4 如图2-1-11(a)所示,重物由钢丝和铜丝结构悬挂在C点,已知G=200N,铜丝和钢丝的许用应力分别为[σ]1=100MPa和[σ]2=240MPa,α=30°。求铜丝和钢丝的最小直径d1和d2。
解:(1)受力分析,绘制受力图如图2-1-11(b)所示。
(2)列平衡方程,求钢丝和铜丝的拉力。
铜丝所受的拉力为FN1=G=200N
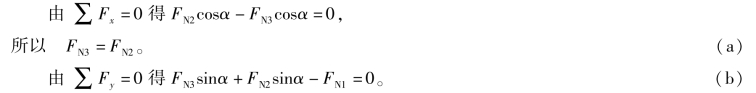
将式(a)代入式(b)解得
![]()
(3)求铜丝和钢丝的最小直径d1和d2。
由强度条件得
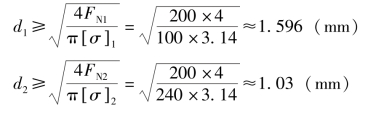
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




