当空间任意力系平衡时,它在任意平面上的投影所组成的平面任意力系也是平衡的。因而在机械工程中,常将空间力系投影到三个坐标平面上,画出构件受力图的三视图,分别列出它们的平衡方程,同样可解除所求的未知量。这种将空间问题简化为三个平面问题的研究方法,称为空间问题的平面解法。本方法适合于求解轮轴类构件的平衡问题。
在应用空间力系的平衡方程解题时,其方法和步骤与平面力系相似,即先确定研究对象,进行受力分析,作出受力图,然后建立合适的坐标系,列出空间力系平衡方程并解出待求的未知量。
例1-5-5 某转轴如图1-5-12(a)所示。已知带紧边拉力FT=5kN,松边拉力Ft=2kN,带轮直径D=160mm,齿轮分度圆直径为d=100mm,压力角(齿轮啮合力与分度圆切线间夹角)α=20°,求齿轮圆周力Ft、径向力Fr和轴承的约束反力。
解:由图1-5-12可知,转轴共受8个力作用,为空间任意力系。对于空间力系的解法有两种:一是直接应用空间力系的平衡方程求解;二是将空间力系转化为平面力系求解,即把空间的受力图投影到三个坐标平面,画出主视、俯视、侧视三个方向的受力图,按平面力系讨论,分别列出它们的平衡方程,同样可解出所求的未知量。本题用两种方法分别求解。
方法一:
(1)受力分析。取传动轴为研究对象,画出受力图,如图1-5-12(a)所示。
(2)建立坐标系。建立图1-5-12(a)所示坐标系。
(3)列方程求解。由式(1-5-8)写出平衡方程。
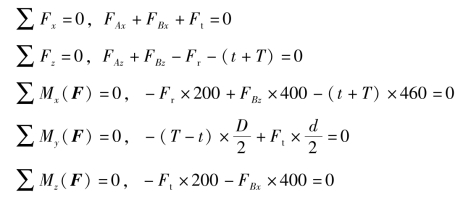
解得(https://www.xing528.com)
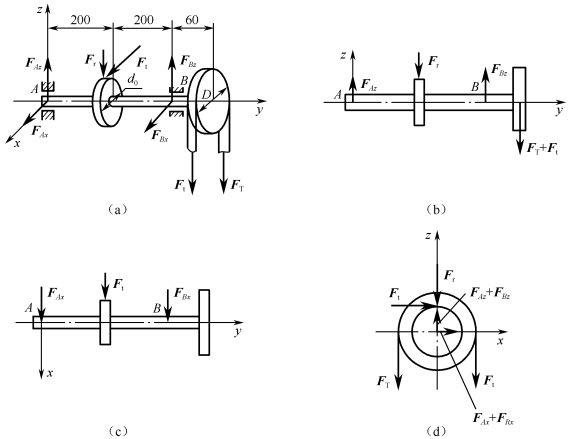
图1-5-12 转轴的受力分析
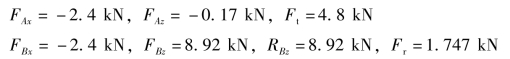
方法二:
(1)受力分析。取传动轴为研究对象,并画出它的分离体在三个坐标平面投影的受力图,如图1-5-12(b)、(c)、(d)所示。
(2)建立坐标系。按所在的平面建立坐标系,如图1-5-11(b)、(c)、(d)所示。
(3)列方程求解。分别在xz、yz、xy面按平面力系平衡问题进行计算。
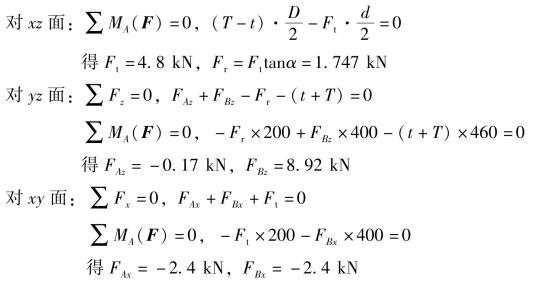
比较这两种方法可以看出,后一种方法把空间力系问题转化为平面力系问题,较易掌握,尤其适用于轮轴类构件的平衡问题的求解。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




