力的投影与分解

1.空间力系的概念

空间力系是各力的作用线不在同一平面内的力系。这是力系中最普遍、最一般的情形。许多工程结构和机械构件都受空间力系的作用，如车床主轴、起重设备、高压输电线塔和飞机的起落架等所受的力均属于空间力系。设计和分析这些结构时，都要应用空间力系的简化和平衡理论。

空间力系的主要类型有：各力的作用线汇交于一点时，称为空间汇交力系，如图1-5-2（a）所示；当各力作用线相互平行时，称为空间平行力系，如图1-5-2（b）所示；若各力的作用线在空间任意分布，既不全部汇交也不全部平行，则该力系称为空间任意力系，如图1-5-2（c）所示。

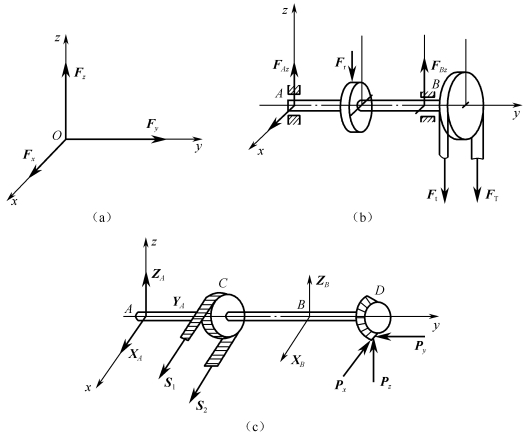
图1-5-2　空间力系

2.力在空间直角坐标轴上的投影

1）直接投影法

力在空间直角坐标轴上的投影定义与在平面力系中的定义相同。若已知力与轴的夹角，就可以直接求出力在轴上的投影，这种求解方法称为直接投影法。

设空间直角坐标系的三个坐标轴如图1-5-3所示，若力F与x、y、z轴正向的夹角α、β、γ为已知，由图1-5-3（a）可知，力F在三个坐标轴上的投影等于力的大小乘以该夹角的余弦，即

图１ -５ -３　直接投影法

力在轴上的投影为代数量，其正负号的规定：从力的起点到终点若投影后的趋向与坐标轴正向相同，力的投影为正；反之为负。而力沿坐标轴分解所得的分量则为矢量。虽然两者大小相同，但性质不同。这是因为力在平面上的投影不能像在轴上的投影那样简单地用正负号来表明，而必须要用矢量来表示。本章中的黑体F表示力F是一个矢量，不仅代表其大小，还代表其方向。

2）二次投影法

当已知力与一个坐标轴的夹角和该力在垂直于该轴的平面的投影与另一轴的夹角时，可采用二次投影法，即先将力投影到一个坐标轴上和该平面上，然后再将这个过渡量进一步投影到所选的坐标轴上。

若已知力F与z轴的夹角为γ、力F在Oxy平面上的投影Fxy与x轴正向的夹角为φ，则力F在x、y、z三轴的投影为

力F的大小、方向为

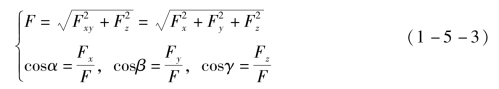
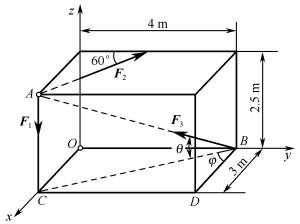
图1-5-4　例1-5-1图

例1-5-1　在长为4m、宽为3m、高为2.5m的长方体上作用有三个空间力，如图1-5-4所示，其中F1＝500N，F2＝1000N，F3＝1500N，求各力在3个坐标轴上的投影。(www.xing528.com)

解：依题意有

（1）F1与z轴平行，故采用直接投影法即可得到

（2）F2与坐标平面Oxy平行，故采用直接投影法即可得到

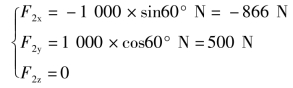
（3）F3为空间力，可采用二次投影法求解。

首先将F3投影到z轴得到F3z，投影到坐标平面Oxy上得到F3xy，然后再将F3xy投影到x轴和y轴上。

由图1-5-4可知，

第一次投影：

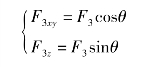
第二次投影：

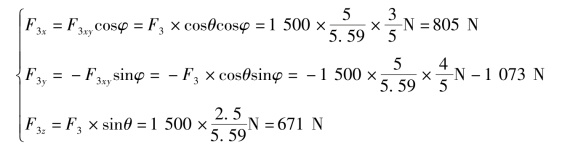
3.力在空间直角坐标轴上的分解

一个空间力可分解为互相垂直的三个分力。例如有一个力F，取空间直角坐标系Oxyz（见图1-5-3），以F为对角线作平行正六面体，根据力平行四边形法则，先将力F分解为两个分力，即沿z轴方向的分力Fz和垂直于z轴平面内的分力Fxy。然后进一步将Fxy分解为沿x轴方向的分力Fx和沿y轴方向的Fy。三个分力Fx、Fy和Fz的大小分别等于力F在x、y、z轴上的投影的绝对值。

例1-5-2　图1-5-5（a）所示为斜齿圆柱齿轮，传动时受到啮合力F的作用，已知F＝7kN，α＝20°、β＝15°，求F的三个分力圆周力Fy、径向力Fr和轴向力Fx。

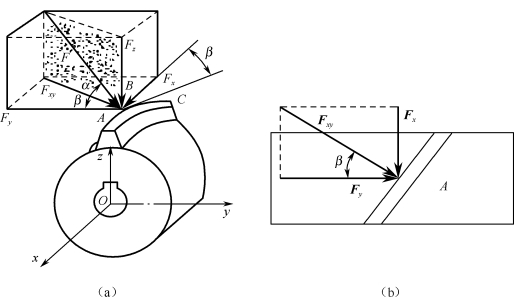
图1-5-5　例1-5-2图

解：建立以力F为对角线的正六面体可得图1-5-5（a）所示直角坐标系Oxyz，分别将啮合力F向平面坐标Oxy和z轴分解，得到Fxy和径向力Fr；再将Fxy向x、y轴上分解，分别得到轴向力Fx和圆周力Fy，如图1-5-5（b）所示。

圆周力：Fy＝Fxycosβ＝Fcosαcosβ＝6.35kN

径向力：Fr＝-Fsinα＝-2.39kN

轴向力：Fx＝Fxysinβ＝Fcosαsinβ＝1.70kN