简化平面任意力系

1.平面任意力系向一点简化

各力的作用线位于同一平面内，既不平行又不汇交于一点的力系，称为平面任意力系。如图1-4-2（a）所示，设作用于刚体上A1，A2，…，An点的平面任意力系F1，F2，…，Fn。在力系所在平面内任选一点O，称为简化中心。根据力线平移定理将力系中各力向O点平移，于是原力系就简化为一个平面汇交力系F1′，F2′，…，Fn′和一平面力偶系M1，M2，…，Mn[见图1-4-2（b）]。

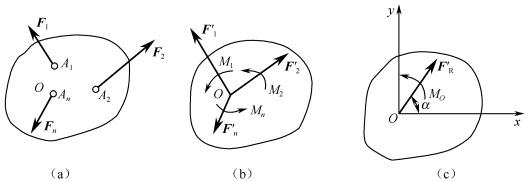
图1-4-2　平面任意力系的简化

1）力系的主矢

平移力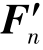，，…，组成的平面汇交力系的合力，称为平面任意力系的主矢。由平面汇交力系的合成可知，主矢等于各分力的矢量和，作用在简化中心上[见图1-4-2（c）]。主矢的大小和方向为

式中　α——主矢与x轴间所夹锐角，主矢的指向由∑Fx和∑Fy的正负决定。

2）力系的主矩MO

附加力偶M1，M2，…，Mn组成的平面力偶系的合力偶矩MO，称为平面任意力系的主矩。由平面力偶系的合成可知，主矩等于各附加力偶矩的代数和。由于每一附加力偶矩等于原力对简化中心的力矩，所以主矩等于各分力对简化中心力矩的代数和，作用在力系所在的平面上[见图1-4-2（c）]，即

综上所述，平面任意力系向平面内任一点简化，得到一主矢和一主矩MO，主矢的大小等于原力系中各分力在两个坐标轴上投影的代数和的平方再开方，作用在简化中心上，其大小和方向与简化中心的选取无关。主矩等于原力系中各分力对简化中心之矩的代数和，其值与简化中心的选取有关。

2.平面任意力系简化结果的讨论

平面任意力系向平面内任一点简化，得到一主矢和一主矩，但这并不是力系简化的最终结果，简化结果通常有以下4种情况。

（1）。由力线平移定理的逆过程可知，主矢和主矩MO也可以合成为一个力FR，这个力就是平面任意力系的合力。所以，力系简化的最终结果是合力FR，且大小和方向与主矢相同，其作用线与主矢平行，并且两者相距d＝MO/（见图1-4-3）。

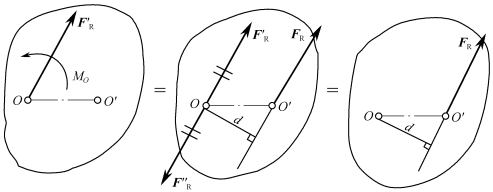
图1-4-3　平面任意力系的简化结果

（2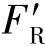）≠0，MO＝0。因为MO＝0，则主矢就是力系的合力FR，其作用线通过简化中心O。

（3）＝0，MO≠0。此时，表明原力系与一个力偶系等效，主矩大小与简化中心的选取无关。(www.xing528.com)

（4）＝0，MO＝0。物体在该力系作用下处于平衡状态，原力系为平衡力系。

例1-4-1　图1-4-4所示为一平面任意力系，每方格边长为16cm，其上A、B、C点的作用力分别为F1＝F2＝16N，F3＝F4＝16N。试求力系向O点简化的结果。

解：（1）选O点为简化中心，建立图1-4-4（a）所示坐标系，求力系的主矢和主矩。

图1-4-4　例1-4-1图

主矢的大小

主矢的方向

主矩的大小

主矩的转向为逆时针方向。

力系向O点的简化结果如图1-4-4（b）所示。

（2）由于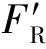≠0，所以力系可合成为一合力FR，即

合力FR的作用线到O点的距离d为

如图1-4-4（c）所示，力系的合力FR的作用线通过A点。