力的平移定理简介及应用

设力F作用于刚体上的A点，如图1-3-13（a）所示，根据加减平衡力系公理，若在O点加上一对平衡力F′、F″，如图1-3-13（b）所示，与原力F等效。力F与F″又形成一对力偶，其力偶矩为M＝Fd＝MO（F）。另一力F′则可看做是力F平移至O点的结果，如图1-3-13（c）所示。

由推证可得：作用于刚体上的力可平移至该刚体上的任一点，但必须附加一力偶，该力偶的矩等于原力对平移点O之矩，此即为力的平移定理。

图1-3-13　力的平移定理

如图1-3-14所示，用丝锥攻螺纹时，要求双手用力均匀，这时丝锥只受一个力偶作用。若两手用力不均或单手用力[见图1-3-14（a）]，则将力平移至丝锥中心后，将得到一个力和一个力偶[见图1-3-14（b）]，该力偶固然能起到攻螺纹的作用，但该力F′将使丝锥发生弯曲，极易使其折断，故应当避免。

图1-3-14　丝锥

【任务实施】

平面连杆机构在图1-3-15（a）所示位置平衡，已知O1A＝40cm，O2B＝60cm，α＝45°，β＝90°，作用在摇杆O1A上的力偶矩M1＝10N·m，不计杆自重，求力偶矩M2的大小。

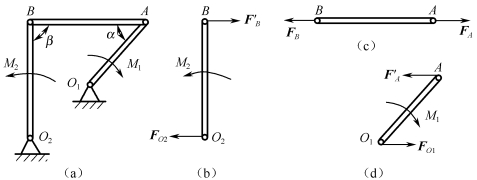
图1-3-15　平面连杆机构的力偶

解：（1）受力分析。连杆AB为二力构件，其受力如图1-3-15（c）所示。由作用力与反作用力公理可确定，O1A、O2B在A、B点的力、的方向。

根据力偶只能与力偶平衡，O2B杆上作用有力偶M2，所以作用在O2B杆O2和B两点的力FO2和一定为一对力偶，绘制O2B杆的受力图如图1-3-15（c）所示。

同理，O1A杆上作用一个力偶M1，所以作用在杆O1、A两端点上的力FO1、F′A一定为一对力偶，绘制O1A杆的受力图如图1-3-15（d）所示。

（2）列平衡方程求解。

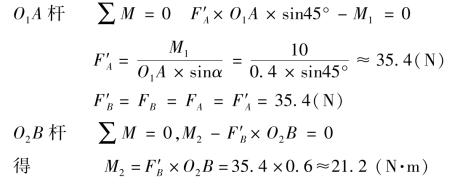(www.xing528.com)

【任务小结】

本任务的主要内容是平面力偶系的平衡问题及其在实际工程中的应用。

1.力对点之矩

力使物体产生转动效应的量度称为力矩。

2.合力矩定理

合力对某点的力矩等于力系中各分力对同点力矩的代数和。

3.力偶及其性质

一对大小相等、方向相反、作用线平行的两个力称为力偶。

性质1：力偶在坐标轴上的投影为零。力偶只能用力偶来平衡。

性质2：力偶对其作用平面内任一点的力矩恒等于其力偶矩。

4.力线平移定理

作用于刚体上的力，可以平移到刚体上的任一点，得到一平移力和一附加力偶，其附加力偶矩等于原力对平移点的力矩。

【实践训练】