力对点的矩及合力矩定理

1.力对点之矩的概念

力对点之矩，是力使物体绕某点转动效应的度量。经验告诉我们，力使刚体绕某点转动的效应，不仅与力的大小及方向有关，而且与该点到该力的作用线的距离有关。例如，用扳手拧紧螺母时，扳手绕螺母中心O转动（见图1-3-2），螺母的转动效应除与力F的大小和方向有关外，还与点O到力作用线的距离d有关。距离d越大，转动的效果就越好，且越省力；反之则越差。显然，当力的作用线通过螺母的转动中心时，则无法使螺母转动。由此，我们引入平面内力对点之矩的概念，用以度量力使物体绕一点转动的效应。

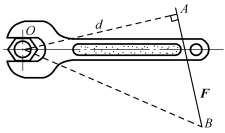
图1-3-2　力对点之矩的概念

平面力F对O点之矩是一个代数量，O点称为矩心，矩心到力作用线的垂直距离d称为力臂。力F对O点之矩用符号MO（F）表示

由式（1-3-1）可知，力矩的大小等于F与O点到力作用线的垂直距离d的乘积，其正负规定为：力使物体绕矩心有逆时针转动效应时，力矩为正，反之为负。力矩的单位是N·m或kN·m。

2.合力矩定理

如图1-3-3所示，由力的可传递性原理，将作用于刚体上A点的力F可以沿其作用线移动到矩心O到力F作用线的垂足B点，而不改变其作用效应。将作用在B点的力可以分解为正交分力Fx、Fy。

图1-3-3　合力矩定理

由图1-3-3可知，合力F和两分力Fx、Fy对O点的矩分别为

由上式可知

上式表明：合力对某点的力矩，等于各分力对该点力矩的代数和。这就是合力矩定理。该定理不仅适用于两个分力的情况，而且适用于多个分力的情况；不仅适用于平面力系，而且适用于空间力系。将上式写成一般通式为

因此，求一个力对某点的力矩，一般采用以下两种方法：

（1）用力和力臂的乘积求力矩。这种方法的关键是确定力臂d。需要注意的是，力臂d是矩心到力作用线的距离，即力臂一定要垂直力的作用线。

（2）用合力矩定理求力矩。工程实际中，有时力臂d的几何关系较复杂，不易确定时，可将力在力的作用线和矩心所确定的平面内，正交分解为两个分力，然后应用合力矩定理求力对矩心的矩。(www.xing528.com)

例1-3-1　如图1-3-4所示，直齿圆柱齿轮的齿面受一压力角α＝20°的法向压力Fn的作用，Fn＝1kN，齿面分度圆直径d＝160mm。试计算力Fn对轮心O之矩。

图1-3-4　直齿圆柱齿轮

解：（1）直接计算。如图1-3-4（a）所示。

（2）按合力矩定理计算。将力Fn分解为径向力Fr与圆周力Ft，Fr＝Fsinα，Ft＝Fsinα

由式（1-3-2）得

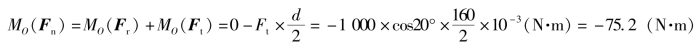
计算结果为负号，表示力矩使齿轮顺时针旋转。

例1-3-2　如图1-3-5所示，货箱重为G，求水平力F应为多少时货箱才能平衡。

解：（1）将力F分解为与货箱两边相平行的分力F1与F2，F1＝Fcosα，F2＝Fsinα。

（2）将力G分解为与货箱两边相平行的分力G1与G2，G1＝Gsinα，G2＝Gcosα。

（3）根据式（1-3-2），得

（4）若要使货箱平衡则需

所以

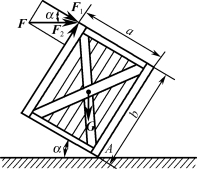
图1-3-5　例1-3-2图