力的分解与投影技巧

1.力的分解

由力的平行四边形公理可知，作用在刚体上，作用线交于一点的两个力，可以合成为一个合力，反过来，围绕一个力作平行四边形，可以把一个力分解为两个力，如图1-2-2所示。力的分力是矢量，有大小、方向和作用点。

根据矢量分解公式有

若将力分解为两个相互垂直的分力，则称为正交分解。如图1-2-3所示，Fx和Fy即力F的两个正交分力。

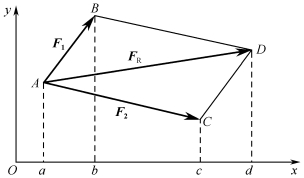
图1-2-2　力的分解与力的投影

图1-2-3　力的正交分解

由图1-2-3可知，力的两个正交分力为

2.力的投影

如图1-2-3所示，在力F作用线所在平面内任取直角坐标系Oxy，过力F的两端点A和B作x，y轴的垂线，得垂足a、b及a′、b′，带有正负号的线段ab与a′b′分别称为力F在x，y轴上的投影，记作Fx、Fy。

力在轴上的投影是代数量，投影有大小和正负。其正负号的规定为：从始端A的投影a（或a′）到末端B的投影b（或b′）的指向与坐标轴的正向相同时，投影为正，反之为负。

投影与力的大小及方向有关，若力F与x轴所夹的锐角为α，则该力在x和y轴上的投影分别为

由式（1-2-2）、式（1-2-3）可知，力在两个直角坐标轴上的投影和力沿两个直角坐标轴方向的正交分力大小相等。若已知力F在坐标轴上的投影Fx和Fy，也可求出该力的大小和方向角α。

式中　α——力F与x轴所夹的锐角，力F方向由Fx，Fy的正负号决定。

注意：力在坐标轴上的投影不一定等于力沿轴的分力，只有当力向直角坐标轴投影时，其投影值与它沿同一坐标轴的分力在数值上相等。(www.xing528.com)

例1-2-1　如图1-2-4所示，试分别求出各力在x轴和y轴上的投影。已知F1、F2、F3、F4、F5、F6大小均为100kN，方向如图1-2-4所示。

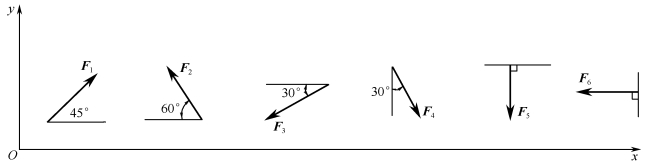
图1-2-4　例1-2-1图

解：由式（1-2-3）可得出各力在x，y轴上的投影。

（1）各力在x轴上的投影：

（2）各力在y轴上的投影：

3.合力投影定理

由力的平行四边形公理可知，作用在刚体上，作用线交于一点的两个力，可以合成为一个力，其合力符合矢量加法法则，如图1-2-2所示，作用在A点的两个力F1、F2，其合力FR等于F1、F2的矢量和。在力系作用面内建立平面直角坐标系Oxy，将合力FR及各分力F1、F2分别向x、y轴进行投影得FRx＝ad，F1x＝ab，F2x＝ac。

由图1-2-2知

故

同理可得

将上述关系式推广至由n个力组成的平面汇交力系，可得

即力系的合力在某一轴上的投影等于各分力在同一轴上投影的代数和，这就是合力投影定理。