微光分辨力理论研究：新发现与未来展望

1.原理

微光夜视技术是在黑夜或暗处条件,实现光电图像信息相互转换、增强、处理和显示等物理过程的技术,微光像增强器(夜视仪)是具有代表性的技术产品。三代微光像增强器[1]由光电阴极、微通道板(Microchannel Plate,MCP)和荧光屏组成,其质量好坏主要取决于总体极限分辨力,故分辨力理论计算模型的精确性很大程度上影响其生产效率、质量及优化方向。在微光像增强器各个部件中,对于GaAs负电子亲和势(Negative Electron Affnity,NEA)光电阴极的研究比较深入,目前研究对象主要为均匀掺杂和变掺杂NEA GaAs阴极,已有不少文献对这两种阴极的电子发射特性做了研究[2～7]。从研究结果来看,无论是均匀掺杂还是变掺杂其极限分辨力都在800 lp/mm以上[8～10],远大于现有的微光像增强器的极限分辨力,可知阴极并不是影响微光像增强器分辨力的主要部件,需要将其各部分联系进行整体研究。YAN Lei等[11]提出一种使用蒙特卡洛方法来计算微光像增强器调制传递函数[12,13](Modulation Transfer Function,MTF)的研究成果,其采取的方法是计算出各个部分的MTF再将其依次相乘来计算出总的MTF,而阴极MTF一般取为1,所得结果没有考虑阴极的影响,且由于阴极内部电子运动情况复杂,之前的研究普遍将阴极电子出射角度按照朗伯体分布处理[14,15],导致结果会损失一部分精度,误差率在10%以上。WU Mei-juan等提出基于蒙特卡洛方法的模型[16],但其同样将阴极电子出射角度按照朗伯体分布处理,虽然模拟结果与实验结果相差较小,但实验数据[17]的精度并不高,故其模型可靠性无法得到保证。

本文考虑了阴极的影响,基于电子在阴极内部运动模型仿真得出的出射分布,建立电子从阴极面发射到荧光屏的运动模型,包括前、后近贴及MCP通道运输模型。通过仿真得到电子运输轨迹及荧光屏上的落点圆斑,最后用蒙特卡洛方法得出MTF及其对应的微光像增强器极限分辨力。本文研究对微光像增强器系统设计具有指导意义,其工作原理示意如图5.22所示。

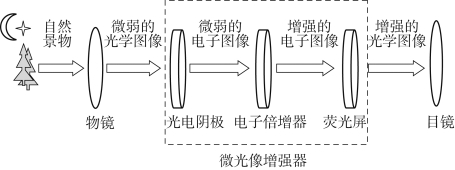
图5.22　工作原理示意

2.阴极体内电子运输模型

电子运输模型包括电子在阴极内,前、后近贴及微通道板通道内的运输模型。首先研究GaAs阴极体内的运输模型[10～18]。

考虑到强电场作用、声子散射以及势垒表面反射等各种因素的作用,电子在阴极内部的传输较为复杂。本研究略去了次要因素,只考虑影响电子阴极出射分布的两个主要因素:一个是弹性散射;另一个是晶格振动造成的能量损失,其设置为与电子移动的轨迹距离呈线性关系。

设GaAs材料掺杂Be原子,Ga0.5N-1 As0.5NBe为均匀掺杂光电阴极的基本结构单元,其中N为基本结构单元中Ga原子和As原子浓度与掺杂原子Be的浓度之比,利用卢瑟福散射理论来模拟光电阴极体内光电子散射,得出其散射公式为

式中:E0是光电子散射前的能量,单位为eV;b e是Be原子到光电子运动路径延长线的垂直距离,单位为nm。

根据电子在均匀掺杂GaAs阴极的运动散射理论公式,建立电子在阴极体内的运动仿真模型。考虑不同波段(400～900 nm)的光所激发的光电子数量在阴极不同位置有所差异,根据不同波段激发的光电子数与吸收位置的关系,通过模拟阴极体内光电子的运输过程,仿真得出电子的出射角度。取光电阴极发射层厚度为2.3μm,窗口材料GaAlAs厚度为1.5μm,光电阴极Be掺杂浓度为1.2×1 019 cm-3,得出光电阴极电子出射角度分布,与朗伯体分布对比,如图5.23所示。其中电子出射角度α从-90°到90°以步长3°变化,n/N为出射角度α的电子数与总电子数比值。

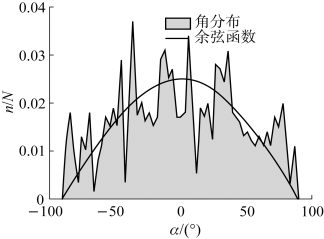
图5.23　阴极电子出射角分布

图5.23表明电子出射角分布与朗伯体分布接近,但仍存有较大的浮动差异,将其分布数据保存,作为理论模型的阴极电子出射分布函数处理。

GaAs光电阴极电子的出射能量分布模型目前较为流行的有Beta分布模型[14]及Maxwell分布模型[19]。但由于在像增强器近贴系统中Maxwell分布模型表现较差,故本模型选用较符合实际的Beta分布[20],即

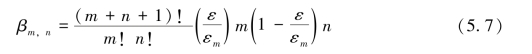
对于均匀掺杂GaAs阴极来说,取m=1,n=8时比较符合实际情况。

3.阴极体外电子运输模型

(1)微通道板内电子运输模型。

与电子在阴极内部的运输模型类似,微通道板内电子的运输过程也较为复杂,不仅要考虑管壁材料电子发射特性,还需考虑末端电极、管壁电荷[21]对电子轨迹的影响,为了方便建模,本文只考虑非异常工作情况下的主要因素。光电子运输到MCP发射材料表面与其有一定的入射角γ,其次级发射电子能量En可表示为

式中:Em为次级发射电子的最大能量。

MCP通道内壁中次级电子发射前几乎各向同性,基本可认为不同发射角度对应的光电子数服从余弦分布。通道壁发射的次级电子数目表示为

式中:N(En,ε)为不同发射能量的光电子数目[22]。

(2)近贴系统电子运输模型。

近贴系统适用于阴极与MCP入射端及MCP出射端与荧光屏之间,可以近似看成由纵向均匀电场构成,由于在运动过程中只在纵向受力,期间形成抛物线轨迹,易求得落点速度及位置物理信息。当电子以初速度v0与法线夹角θ0射出并纵向位移L距离时,其在z、r方向的速度与位移可表示为

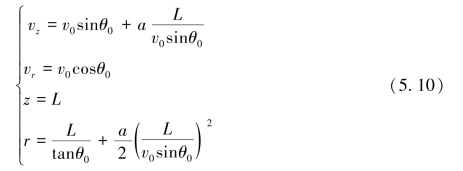(www.xing528.com)

式(5.10)可以确定电子在荧光屏上落点分布情况,由此计算调制传递函数[23],即

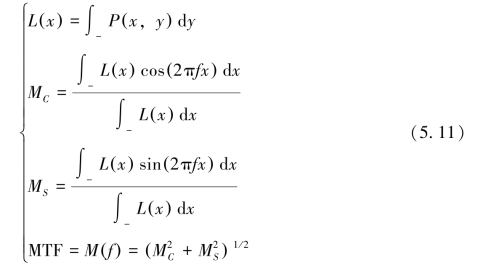
式中:P(x,y)是荧光屏像面上的光强度;L(x)为线扩散函数。

对线扩散函数做离散傅里叶变换,计算得到调制传递函数。

4.仿真结果

为了便于对比,设置与文献[16]相同的参数。设前近贴距离D1=150μm、MCP长度距离D2=254μm、第二近贴距离D3=400μm、前近贴电压V1=800 V、微通道板两端电压V2=1 000 V、后近贴电压V3=5 000 V,微通道板通道直径d由6μm变化到12μm,步长为2μm。模拟光电阴极受激出射电子,光电子的角度变化范围为-89°～89°,步长为2°,能量变化范围为0.2～1.0 eV,步长0.03 eV,得到电子运动轨迹如图5.24所示。

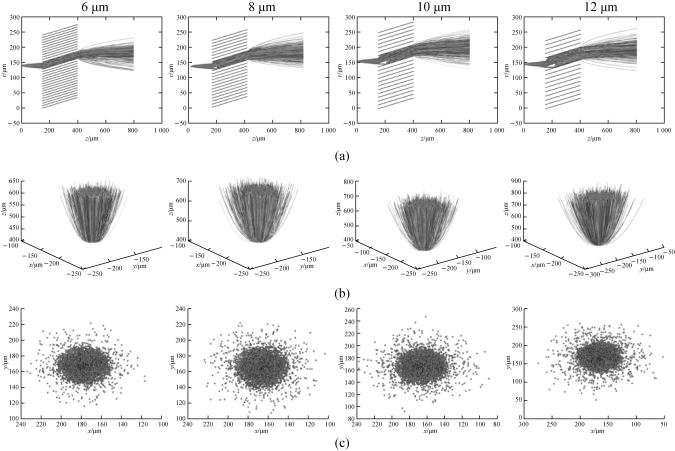
图5.24　不同MCP管径的电子运输轨迹仿真

(a)二维电子轨迹;(b)后近贴三维电子轨迹;(c)荧光屏电子分布

图5.24(a)以二维方式展示了阴极某点出射电子在前、后近贴及MCP管壁中的运动,直到荧光屏处消失;随着MCP通道直径的增加,其通道出口处的电子束会趋于发散,如图5.24(b)所示;最终其在荧光屏形成的电子圆斑也会依次增大,如图5.24(c)所示。由荧光屏上电子圆斑的分布情况,计算每种像增强器对应的MTF曲线,如图5.25所示,显然在相同的MTF下,微通道板通道直径越小,其所对应的空间频率越大,取MTF=0.3即可求得对应极限分辨力。

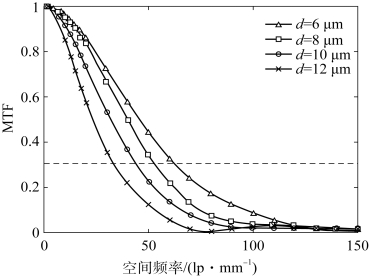
图5.25　不同参数对应的MTF曲线

5.实验及结果对比

如图5.26所示,用实验来对理论模型进行验证,仪器包括光源、平行光管、USAF1951靶、像增强器和CCD相机,实验使用的是RES-1分辨率测试靶(部分透明),由NEWPORT公司提供。卤素钨灯发出白光束,经过中性滤光片及可变光阑后才到达平行光管(F=1 000),在穿过平行光管后,光束以2 933 K的色温穿过测试靶并将分辨力靶图案投射在被测像增强器的阴极入射面上,最后通过观察CCD相机(2 416万像素)上线对的数量,在靶标分辨力查找表找到对应的分辨力。

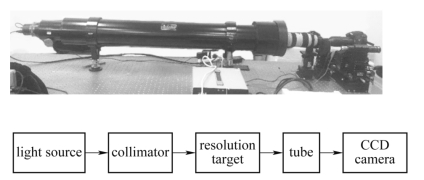
图5.26　实验装置

光束的光强为1×10-4～1×10-3 lx,且有效光照区域的光强不均匀度不超过1.5%,可以保证结果的有效性。测试了4组不同型号的像增强器(北方夜视公司提供),其MCP的通道直径从6μm到12μm以2μm步长依次增加,其他参数如阴极参数、电压、距离和MCP长度参数与仿真所用参数保持一致,观测结果如图5.27所示。

随着通道直径的增加,可识别的线对数量不断减少,在通道直径达到12μm时不能区分第7单元的任何线对。而在通道直径减小至6μm时,已经能辨认第7单元的所有线对。通过靶标分辨力查找表,得到了4个像增强器的极限分辨力,与本文模拟结果进行对比,如表5.10所示。

图5.27　像增强器能清晰辨认的对线数图片

(a)识别对线数(6μm);(b)识别对线数(8μm);(c)识别对线数(10μm);(d)识别对线数(12μm)

表5.10　仿真结果与实验结果

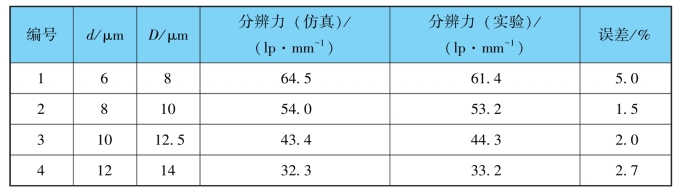
由表5.10可知分辨力测量结果与实验结果的误差非常小,最大误差仅为5.0%,远小于已有模型结果的10%以上的误差。将参考文献[16]中的结果与本文实验结果进行比对并计算误差,与模拟结果比较如图5.28所示。

图5.28分别用“(1)”和“(2)”指代本文模型与参考文献[16]模型,横坐标为像增强器型号。图5.28(a)结果显示本文模拟结果较参考文献[16]更贴近测量结果,参考文献[16]中的模拟结果与本文实验结果对比其最大误差可达10.7%,如图5.28(b)所示。且本文模型随着MCP管径参数的改变,所得分辨力的大小变化一致,证明该模型拥有精确性和较好的泛化能力。

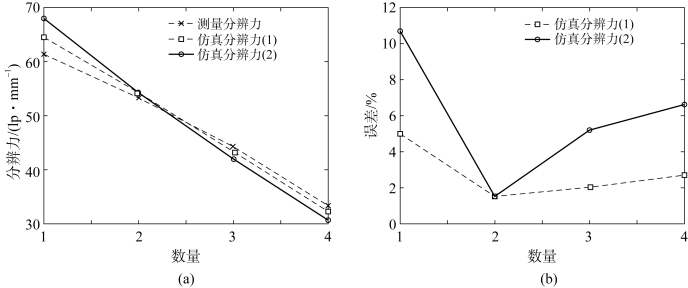
图5.28　仿真和实验分辨力结果

(a)仿真和实验分辨力;(b)仿真分辨力误差