探究理想积分球特性的研究

基于漫反射原理,设计一种基于球面的反射面,即理想的积分球,这样就能使得光源发出的光在球面的内壁达到无穷次的漫反射。理想积分球是封闭的空腔圆球,球内表面涂有白色中性的漫反射涂层,理想积分球要符合3个条件:①它是内部空心的球体;②球体内没有任何吸收光线的物体;③内壁涂层反射比应该是中性的,如硫酸钡[30～32]。理想的积分球原理示意如图1.53所示。

图1.53　理想积分球原理示意

在图1.53中L是光源,光源L可以放在理想积分球内的各个位置。设理想积分球的圆心为O,理想积分球内表面的漫反射涂层的反射比为ρ,理想积分球的半径为R,光源L的光通量为φ。

在理想积分球内壁上的任一点B的照度E由两部分的照度叠加而成:一部分是光源L第一次照射在点B时得到的照度,另一部分是光源L照射在理想积分球内壁上的除点B以外的所有点(其中一点如A点)后,经过漫反射照射在点B所得到的照度。漫反射到B点的照度包括一次漫反射得到的照度,两次漫反射得到的照度,以至无穷次反射之后所得到的照度。

光源L第一次照射在点B时得到的照度为

式中:Ed为光源L第一次照射在理想积分球内壁上的点B时得到的照度(lx);φ为光源L的光通量(lm);R为积分球的内壁半径(m)。

第一次漫反射后照射在点B时得到的照度直至第无穷次漫反射后照射在点B时得到的照度为

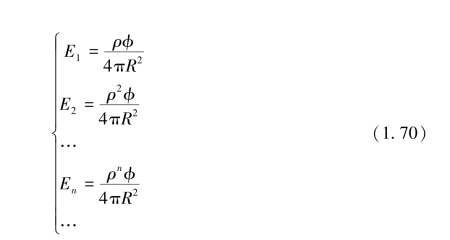(www.xing528.com)

式中:Ei(i=1,2,…,n,…)为每次漫反射后照射在理想积分球内壁上的点B时的照度(lx);ρ为积分球内壁漫反射层的反射比。

则理想积分球内壁上的点B的照度为

式中:E为理想积分球内壁上的点B的照度(lx)。

式(1.71)的第一项就是光源L直接照射在理想积分球的照度。根据光源的各向异性,直接照射在点B所得到的照度与光源的方向有关系,这个直接照射在点B所得到的照度是一个随方向改变而变化的变量。为了使得点B所得到的照度不受这种光源各向异性的影响,可以在光源L与点B之间设置一个挡光屏,挡住光源L的直射光,带挡光屏的积分球原理如图1.54所示。

图1.54　带挡光屏的积分球原理图

理想积分球加了挡光屏之后,则式(1.71)转化为

由式(1.72)可知,光源L发出的光经过带挡光屏的积分球内壁无穷次的漫反射之后,在积分球内壁部分区域会存在均匀的照度。积分球内壁上均匀照度区域的照度仅与3个量有关系,即光源L的光通量φ、积分球的半径R以及积分球内表面的漫反射涂层的反射比ρ。