分析传统与新型热电子面发射源

1.传统热电子面发射源的理论计算与局限性分析

现有的MCP清刷设备(只适用于φ50mm以下的MCP)一般采用的是加热钽灯丝的热电子面发射源(电子枪)来产生均匀电子束。根据MCP的清刷机理可知,电流密度与电子束均匀性是热电子面发射源的两大核心指标,现围绕这两大指标对传统热电子面发射源进行理论上的建模分析。图1.34为传统热电子面发射源的结构剖面图[21]。

图1.34　传统热电子面发射源的结构剖面图

1,2—热电子面发射源外壳;3—真空腔室转盘;4—待清刷MCP;5—第二阳极;6—电子散射网;7—灯丝;8—接线座;9—屏蔽盘。

如图1.34所示,该外围电场的结构设计参照了电子光学透镜,第二阳极的电压电位可在-10 000～0 V之间调节,6、7、8、9同电位,为第一阳极,电位可在-10 000～0V之间调节。调节第一阳极与第二阳极的电压可改变该热电子面发射源内部电场分布,从而控制发射电子的运动轨迹,用于得到清刷需要的电子束。热电子面发射源的电子发射密度与均匀性在根本上是由产生发射电子的灯丝所决定的,该灯丝采用了电子逸出功与热导率均较小的钽丝作为材料的平面螺旋型灯丝,下面对灯丝的电子发射密度与均匀性进行理论分析。表1.4给出了钽的热电子发射相关参数[22～23]。

表1.4　钽的电子发射参数表

根据李查生-德施曼公式[24],纯金属在零电场的情况下的热电子发射密度为

式中:J为发射电流密度(A/cm2);A0为发射常数理论值(A·cm-2·K2),数值为120.4;φM为所用金属的逸出功(eV);T为金属温度(K);k为玻耳兹曼常数。

根据传统热电子面发射源的结构可知,平面螺旋型灯丝在真空系统中加热时处在封闭的电场中,而外加电场对金属的热电子发射有影响,现用J0来表示有外加电场下的电子发射密度。根据量子力学原理,并不是所有能量高于表面势垒的电子都能逸出金属,它们仍有被反射回金属的可能。由此引进一个平均反射系数,所以平均透射系数为。这样就可以得到

而式(1.42)中逸出功φM是温度的函数,单位为eV。设逸出功随温度的变化近似为线性关系,即

式中:α为温度影响系数(eV/K);T为温度(K),φOM为初始功函数(eV)。

将式(1.43)与式(1.44)代入式(1.42)可得到

由理论计算可得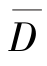约为0.98。根据实验结果,对于钽而言,α≈(6～7)×10-5 eV/K,所以式(1.45)可简化为

从式(1.45)到式(1.46)中用A代替了A0,其中A为实验实测得的发射常数(也称李查生常数)。这是由于发射常数A中包括了平均透射系数和逸出功的温度系数影响,因而其值与理论值A0有较大的偏离。根据相关资料,实测得A值约为55 A·cm2·K2。

传统热电子面发射源采用的是平面螺旋型灯丝,其造型在形状上与阿基米德螺旋线比较相像。通过实际测量,该灯丝相邻两圈间的间距都是相等的,约为1mm,用于制作灯丝的细钽丝直径d为0.3mm,整个灯丝面的直径D约为10mm。根据灯丝的几何特征,将灯丝实物抽象为理论模型,如图1.35所示,以便对灯丝进行数学建模与理论计算。

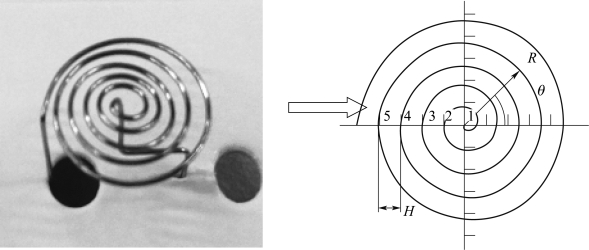
图1.35　平面螺旋型灯丝数学建模示意

根据平面螺旋型灯丝平面示意,图1.35中R是角度为θ时第n圈灯丝的半径,H为相邻两圈灯丝间的距离。现可对灯丝单圈长度进行计算,假设第n圈的灯丝长度为Ln,则有

则第n圈灯丝的电子填充面积Sn为

而灯丝半径R与间距H的关系为

由式(1.46)、式(1.47)、式(1.48)可推导得到平面螺旋型灯丝第n圈的电子发射密度J e为

式(1.50)仅在相邻两圈灯丝距离H较小时成立(H的极限值可由实验测得)。简化式(1.50)可得到

式(1.51)即为平面螺旋型灯丝第n圈的电子发射密度公式,从中可以看出灯丝电子发射密度Je只与灯丝的直径、温度、间距有关。依据该公式,将灯丝的直径及温度参数代入即可计算出传统热电子面发射源灯丝的电子发射密度。所以根据灯丝外围电场对电子的作用得出电子的输出面积与灯丝发射面积的比例关系即可计算出该热电子面发射源的电子发射密度。

由式(1.51)可以看出,平面螺旋型灯丝(将灯丝间距控制在理论范围之内)的空间任何一点的电子发射密度与其空间位置无关,在灯丝外界条件已经确定的情况下,灯丝的电子发射密度一致,也就是说这样形状的灯丝面电子发射具有良好的均匀性。

受限于目前的灯丝制造工艺,加之灯丝在长期使用的过程中由于高温加热会导致一定的变形,使得平面螺旋型灯丝并不能严格保持在同一水平面内。假设灯丝由于制造工艺或者长期受热变形后灯丝的截段正视图如图1.36所示,假设微小的一段长度为d m,该段切线与水平线(理想水平灯丝)的夹角为α。

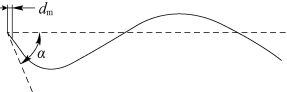
图1.36　变形灯丝截段正视图

理想状态下,假设水平灯丝的对应段长度为d l,则可认为有如下关系为

对于该小段而言,电子发射面积是相同的,所以容易得到该小段变形灯丝的电子发射密度J m的计算公式为

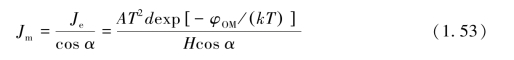
不妨将完整的平面螺旋型灯丝看成由N个d m小段组成,由于α的值在不断的变化之中,所以对于变形的灯丝而言,其每小段的电子发射密度都不相同,这将造成平面螺旋型灯丝平面的热电子发射分布不均,发射电子的均匀性完全取决于α角的数值变化。

根据对传统热电子面发射源的研制经验,灯丝在工作时需要通过2～5 A的电流,灯丝温度达到2 000 K以上。在长时间使用的情况下,灯丝会出现烧蚀、发热变形的问题,这样累积的变形加剧了灯丝发射电子的不均匀性。而目前的加工工艺,灯丝在加工过程中重复精度差,不具备百分之百的复制性,这就导致了不同热电子面发射源间的发射电子均匀性存在差异。

2.新型热电子面发射源的理论计算与研究

鉴于传统热电子面发射源技术的局限性,需要研制适合大面积MCP电子清刷测试系统的新型热电子面发射源。金(Au)阴极作为光电阴极,其发射稳定度高,可多次暴露于大气之中而不改变其发射特性,且光电流密度分布均匀[25]。金阴极在外界紫外光照射的条件下能产生发射电子,并且金阴极在尺寸上并没有限制,所以可利用紫外光照射金阴极产生发射电子的原理来研制新型热电子面发射源。

(1)金阴极介绍。

金阴极是指以石英玻璃材料为基底,石英表面附有金薄膜的具有光电发射特性的阴极。薄膜指1×10-10～1×10-6 m厚的金属、化合物膜层,其物理制备方法有阴极溅射和真空蒸发[26]。金阴极采用了真空蒸发的制备方法,其制备过程如下:将载有高纯度金粉(或丝)的钼舟置于真空腔室内,使其正对石英基片;首先对蒸发源进行严格的除气处理,并将石英基片加热到200℃以上,在真空度达到4×10-3 Pa后,采用真空蒸散法即可实现在石英基片上形成金薄膜。金薄膜属于纯金属层,形成后无须进行任何处理,其化学与热学稳定性好,常温状态下不易被氧化[27～28]。相关研究表明,蒸涂好的膜层在净室内多次暴露于大气后光电流起伏变化不超过1%,金阴极实物图如图1.37所示。

图1.37　金阴极实物图

(2)新型热电子面发射源入射光响应光谱计算。(www.xing528.com)

为了利用金阴极获得较为理想的发射电子束,需要对金阴极的光谱响应特性进行理论分析。金阴极发射电子的原理是其紫外发射特性,即利用一定频率的紫外光照射金阴极使其产生发射电子。

根据量子力学理论,常温下金属内部的电子服从费米(Fermi)分布定律[29～30],即

式中:d N与d Z分别表示在能量区间(W+d W)内粒子数目及量子态数;k为玻尔兹曼常数(J/K);T为温度(K);常数;W f为处于费米能级的电子具有的能量,对于金阴极而言W f=5.5 eV。

对于金属中具有最小初始动能的电子而言,电子在吸收光子能量时处于原子的最低能级上,所以电子必须吸收逸出功与费米能级能量之和(金属表面势垒)的能量才能逸出金属表面,即

式中:为电子的最小初动能(eV);h为普朗克常数,其值为4.14×10-15 eV·s;v1为具有最小初动能的电子需要逸出时所需要入射光的频率(Hz);Wa为金属表面势垒(eV);φ为金属逸出功函数(eV);W f为电子所在的费米能级能量(eV)。

对于金属中具有最大初始动能的电子而言,电子在吸收光子能量时处于原子的最高能级上,并且就在金属表面。所以电子只需吸收能够克服逸出功的函数的能量即可逸出,即

式中:为电子的最大初始动能(eV);ν2为有最大初始能量的电子逸出所需要的入射光频率(Hz)。

以上两种情况是金属内部电子的两种极端情况,对于具有最小初动能的电子来说,初始动能约为0。对于大部分电子而言,其初始能量大小介于最小动能与最大动能之间。所以结合式(1.55)与式(1.56)可得到金属内电子逸出的入射频率ν服从的关系为

根据国外相关文献的研究,金阴极在理想的真空环境中其逸出功函数为4.9 eV,而经常暴露大气后的金阴极其逸出功函数将降至4.3 eV,并以该逸出功函数稳定工作。考虑到清刷测试系统的实际工况,金阴极将不可避免地多次暴露在大气之中,所以可以认为该金阴极的逸出功函数为4.3 eV。图1.38中实线曲线为实验测得的逸出功函数为4.9 eV的金阴极的光谱响应特性曲线[24]。其中横坐标E ph表示入射光子的能量,纵坐标QE表示归一化的量子效率。

图1.38　金阴极的光谱响应特性曲线

从图1.38中实测曲线可以清楚地看出,该金阴极具有明显的选择性光电效应,具有光电效应的入射光子能量绝大部分分布在式(1.57)的计算范围之内(4.9～10.4 eV),与理论计算相吻合。此外,可以注意到在入射光线能量小于4.9 eV的能量段,金阴极有微小的光电效应。理论上,根据爱因斯坦定律,当入射光子能量小于电子逸出功时,无论光强如何、照射时间多长,都不会有光电子产生。而实际上,爱因斯坦定律只是温度T=0时的近似定律,当T≠0时,只要传感器的灵敏度够高,即使入射光子能量小于电子逸出功,也能测得光电子信号,并不存在一个使电子发射截止的阈值频率。从图1.38中的实测曲线还可以看出,金阴极的光电流发射密度具有一个明显的峰值,其对应的电子能量为5.72 eV,在电子能量超过5.72 eV后,金阴极的光电流发射密度急剧下降。这是由于金阴极内部电子在不同能级上分布数量不同而造成的。金阴极在吸收光子能量后逸出到真空能级以上的自由电子随着频率增高而增大,但自由电子吸收光子的概率在入射光频率较高时却随着频率增高而减小[24]。受到这两个因素的共同影响,出现了如图1.38所示的金阴极选择性光电效应。

至于金阴极选择性光电效应的峰值对应的入射光子能量,目前还没有相关的理论可以精确计算。根据对金属电子吸收光子能量逸出的分析,同时考虑到电子在向金属表面运动时由于相互碰撞会损失掉一部分能量,可得到金阴极内电子逸出时能量满足的关系为

式中:为逸出电子的初始能量(eV);v为具有该电子逸出能量的入射光频率(Hz);E s为该电子向金属表面运动由于碰撞损失掉的能量(eV)。

式(1.58)给出了金阴极内一般电子逸出时能量所需要服从的法则,可以看出,对于逸出功函数为4.9 eV与4.3 eV的金阴极在工作时,其他工作环境完全一致,因此其他变量均可认为不发生改变,只是金阴极的逸出功函数发生了改变。由于目前还没有任何实验对逸出功函数为4.3 eV的金阴极进行光谱响应特性的测试,但根据对公式的分析,可以推断得到逸出功函数为4.3 eV的金阴极近似光谱响应特性曲线如图1.38中虚线所示。该曲线所反映的金阴极选择性光电效应为新型热电子面发射源入射紫外光的波长选择提供了理论指导。

入射光的波长选择可根据光子能量计算公式计算得到,该公式为

式中:h为普朗克常数(eV·s);c为光速(m/s);λ为波长(m)。

经过计算可得,逸出功函数为4.3 eV的金阴极对波长为242 nm的紫外光响应将达到峰值状态,若对QE值处于50%以上的入射光波长进行计算,可知紫外光源选取波长约为225～261 nm的波段紫外光比较合理。

而根据金阴极发射稳定度高,且光电流密度分布均匀的特性,理论上只要保证入射光的均匀性,即可得到均匀的发射电子束。至于入射光的均匀性,可通过对紫外光源在形状上的特殊造型来保证。鉴于光电发射的相似性,对于紫外光源的几何形状的设计,根据上一小节的理论推导,平面螺旋造型是一种理想的选择。

(3)发射电子运动轨迹的理论推导。

新型热电子面发射源在解决发射电子的来源问题后,需要对发射电子的轨迹进行计算,为发射电子的加速电场设计及热电子面发射源的结构设计提供理论指导。现假设阴极B与阳极A的空间关系及外界条件如图1.39所示。

图1.39　电子轨迹理论计算模型

如图1.39所示,A代表阳极,B代表阴极,对它们分别施加U a与U b的电压(U a-U b＞0),单位为V,A与B之间的距离为L。E为电场矢量,电子的入射角为α,电子到达阳极后与y轴的距离为H,单位为m。根据以上条件可知,A与B之间将形成均匀电场,且其沿y轴方向上的电位为

当入射电子以E0的初始能量入射时,它的入射角为α,所以电子将在均匀电场中形成抛物线形状的轨迹,根据电子在该电场中的运动规律(电子自身重力忽略不计)可得该曲线上任意一点c的坐标为

式中:t为电子到达点c的时间(t);Vx、Vy分别为电子入射时初速度在x、y轴方向上的分量(m/s);a为电子在该电场中的加速度(m/s2)。

所以根据能量关系,有

式中:e为电子电荷量(C);m为电子质量(kg);Ex、Ey分别为电子入射初始能量E0在x、y轴方向的能量分量(eV)。

将式(1.62)代入式(1.61)化简后得到电子轨迹的运动方程为

当电子运动到阳极时,即x=H,可得

在电子轨迹计算时,在能量上有关系式(U a-U b)e≫Ex及(U a-U b)e≫Ey,所以有

又根据电子速度的关系Vx=V0 sinα可得

所以将式(1.66)代入式(1.65)可得

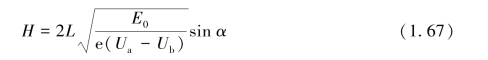
在具体计算时,由于能量的单位为eV,所以在忽略量纲的前提下,可将e视作1,略去不写。而根据发射电子在整个平面各个方向的角度分布(-π/2～π/2),可以得到新型热电子面发射源结构尺寸设计所需计算的电子最大弥散圆半径r max的最终计算公式为

式中:L为阴极与阳极间的距离(m);E0为电子入射初始能量(e V);U a为阳极电压(V);U b为阴极电压(V);电子e电量视为单位1,在公式中已省略。

考虑到金阴极电子发射在数量上与能量上均服从郎伯余弦分布,因此绝大部分发射电子均集中在阴极平面的法向方向附近,这样的电子分布会造成弥散圆半径内的部分区域内电子密度与能量严重失衡,如果待清刷MCP处于这个面积内,将造成MCP的清刷不均匀,这样不仅达不到预期的清刷效果,而且会破坏被清刷MCP的均匀性。因此,在进行新型热电子面发射源的设计时,应尽量控制弥散圆的半径,或者使分布不均的电子不落在待清刷MCP的区域内。从式(1.68)中可以看出,只需保证(U a-U b)≫E0以及将距离L控制在一个比较小的范围内,就可以基本消除电子弥散带来的影响。