热电子面发射源的电场分布和轨迹计算

在确定了灯丝造型的基础上,由于热电子发射的能量为1 eV,激发荧光粉需要几千电子伏特的能量,才能使其发光,所以需要设计电子加速场,根据测试系统测试荧光屏发光均匀性、发光效率和余辉的需要,电子加速场要能够改变热电子的轨迹,使其具备均匀、汇聚和淹没的特性,我们设计了第一阳极、第二阳极的电压分别在-10 000～0 V任意可调的负高压电源,考虑操作安全,转盘和真空外壳电压为0 V,所以设计采用负高压电源;荷兰DEP公司早期像增强器荧光屏测试仪中热电子发射源的结构尺寸,如图1.10所示,它是点发射源,采用正高压,转盘与外壳之间绝缘,采用目视方法判断荧光屏发光的均匀性,存在人为误差,精度不高,不具备其他功能,所以该设备已经落伍。

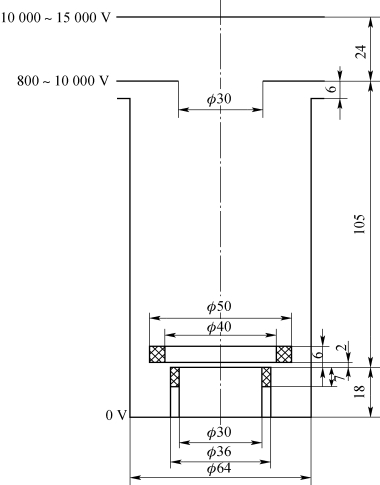
图1.10　DEP公司的热电子发射源的结构

为了控制热电子面发射源发射电子的轨迹,参照电子光学透镜的设计,初步设计出电子发射源的结构,如图1.11所示。图中1为真空部件中的转盘,上面一次可以放置28个直径分别为18mm和25mm的像增强器裸屏(荧光屏),2为荧光屏,电位为0 V,3为第二阳极,电位可在-10 000～0 V之间调节,4为真空外罩,电位为0 V,5为热电子面发射源外壳,6为电子散射网,7为灯座,8为灯丝接线,9为屏蔽盘,6、7、8、9同电位,为第一阳极,电位可在-10 000～0 V之间调节。

其结构属于轴对称静电场结构,下面对其电场分布和电子轨迹进行理论分析和计算。

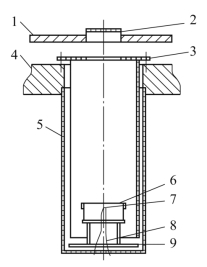
图1.11　热电子面发射源的初步结构

1—转盘;2—荧光屏;3—第二阳极;4—真空外罩;5—热电子面发射源外壳;6—电子散射网;7—灯座;8—灯丝接线;9—屏蔽盘。

1.轴对称静电场的数值计算

在旋转对称静电场的情形下,选用(z,r,θ)圆柱坐标系,并且使z轴与旋转对称轴重合。由于旋转对称性,电位v只是z和r的函数,所讨论的问题在大多数情况下,可以归结为在给定的边界所包围的封闭区域内,求解轴对称型的拉普拉斯(Laplace)偏微分方程为[15～19]

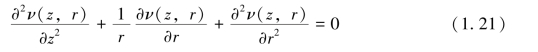
式(1.21)中:z、r分别为轴向和径向坐标。

对于轴上点的电位可简化为数值方法中常用的有限差分法和有限元法两种。有限差分法为

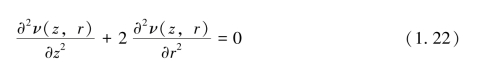
在有限差分法中,把求解区域划分为许多(有限个)正方形或矩形的网格,需要确定函数(电位)值的节点就配置在网格交点上,并用相邻节点的差分来代替拉普拉斯方程中的偏微分,用差商来代替微商,用差分方程来代替偏微分方程,最后建立了所有节点上的电位所应满足的高阶线性代数方程组,求解这个代数方程组,定出各节点上的电位数值,就得到了求解区域的电位分布。所有这些计算过程都可由计算机来完成。只要网格划分得足够细,就能得到足够精确的数值解。

图1.12表示步长为h的等距正方网格。分两种情况:一种是由1、2、3、4点的电位值计算P0点的电位,它的差分公式为

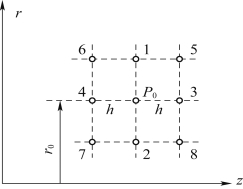
图1.12　等距五点网格图

另一种是由5、6、7、8点的电位计算P0点的电位,差分方程为

一般情况下使用式(1.23)计算,有时用式(1.24)计算子区间边界。

如图1.13所示,轴上点等距三点差分公式为

图1.13　等距三点网格图

如图1.14所示,轴外点不等距五点差分公式为

图1.14　不等距五点网格图

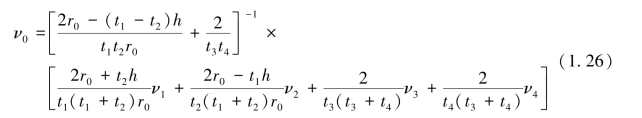
如图1.15所示,轴上点不等距三点差分公式为

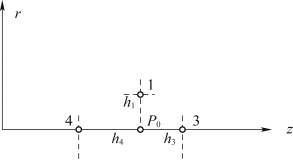
图1.15　不等距三点网格图

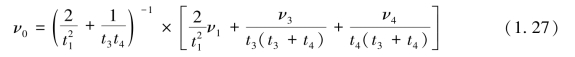
利用差分公式计算电位分布是在封闭边界所围区域内划分的网格节点上进行。由于以轴对称作为前提,因而只需在半个子午面上划分网格并进行计算,大大减少了准备和计算的工作量。

由于节点所处的位置不同,可能要用到上述的不同差分公式。为了便于计算机记忆和识别,需对各点注以标号,以便机器计算到某点时自动提取标号对应的差分公式,这为计算的实施提供了方便。全部节点标号的集合称作逻辑尺,全部节点所赋初值,边界坐标及边值,连同各节点对应的标号称作准备数据表。可见,划分网格,建立逻辑尺及设计填写数据表是计算前必作的准备工作。

差分方程给出后,通常不采用直接求解的方法,而采用迭代方法。为了加快收敛速度,减少迭代次数,通常采用Seidel—Liebmann迭代法。

当给定系统的边界条件和网格节点的初值后,由轴线开始作为第一排,使Z按间隔n由轴线的起点至最远的边界进行逐点计算,完成一排后向Y方向顺序推进一排,如此往复,直至完成子午面上全部网格节点为止。完成一遍的逐点计算后,用新的电位值取代原电位值,再进行新一遍的迭代计算,这样反复地迭代下去,直至两遍的全部节点的电位差值小到满足要求为止。

为了表示迭代过程中电位值的运用,将五点差分及三点差分公式按等距和不等距的格式列在下面,具体公式为

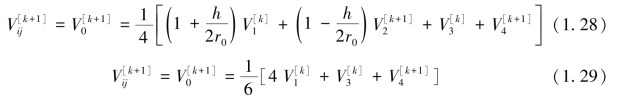
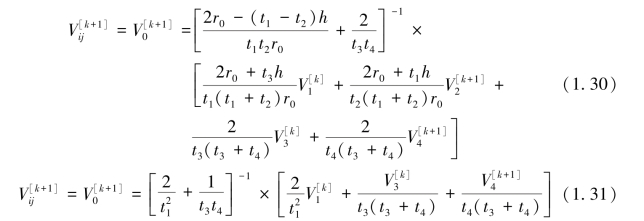
从式(1.28)～(1.31)可以看出,此种迭代方法是将每次算出的新的结果立即取旧值并写入内存,所以对Vij作第K+1次计算时,V1和V3用的是第K次的结果,而V2和V4则用本次(即K+1次)计算的结果。这样,与用4个全部是第K次值的简单迭代法相比,不仅可节省一倍的内存,还可以加速收敛过程。

2.电场计算结果

在理论的指导下,还需要通过试验找到第一阳极和第二阳极需要多少电压,才能使热电子均匀或汇聚或淹没;所以按照初步设计,加工出热电子面发射源的试验品,在真空系统中放置标准荧光屏,分别调节第一阳极、第二阳极电压,得出荧光屏发光的3种典型图像,得到特征电位值。

荧光屏发光不均匀时,第一幅图第一阳极电压值为-4 000 V,第二阳极电压值为0 V,电位分布图为凸电子光学透镜,根据凸电子光学透镜所在位置,热电子具有发散特性,计算出的轴对称静电场电位分布如图1.16所示。横坐标为热电子面发射源直径,单位为mm;纵坐标为热电子面发射源高度,单位为mm。

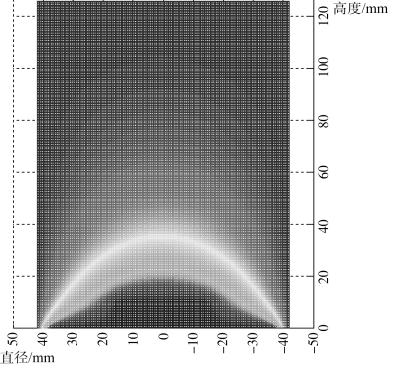
图1.16　发散的电场电位分布图

荧光屏发光基本均匀时,第一阳极电压值为-4 000 V,第二阳极电压值为-2 000 V,计算的电位分布图为两个凸电子光学透镜,灯丝面源直径为5 mm,为了让电子均匀分布在不小于直径为40 mm的圆面上,所以两个凸电子光学透镜焦距不同,根据凸电子光学透镜所在位置,热电子在电场中先发散后汇聚的轨迹特性,最后形成均匀分布的特性,如图1.17所示。横坐标为热电子面发射源直径,单位为mm;纵坐标为热电子面发射源高度,单位为mm。

图1.17　均匀的电场电位分布图

荧光屏发光汇聚成点时,第一阳极电压值为-4 000 V,第二阳极电压值为-3 990 V,电位分布图为凸电子光学透镜,根据凸电子光学透镜所在位置,热电子具有汇聚特性,计算出的轴对称静电场电位分布如图1.18所示。横坐标为热电子面发射源直径,单位为mm;纵坐标为热电子面发射源高度,单位为mm。

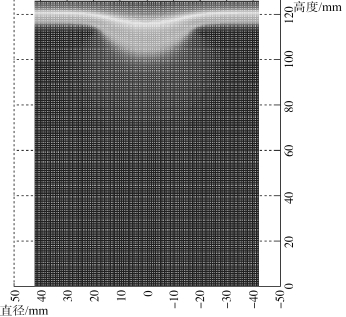
图1.18　汇聚的电场电位分布图

3.电子子午轨迹的计算

旋转对称场中电子轨迹服从子午轨迹方程,依据所求出的电位分布,就可以计算出在给定的初始条件(即电子自阴极面发射出来时的初始位置、初始方向和逸出时的初电位)下,电子轨迹微分方程或运动微分方程的解。电子发射示意如图1.19所示。

子午轨迹是子午平面内的平面曲线,方程为

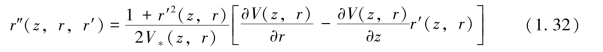
式中:V*(z,r)=V(z,r)+ε为规范化电位。

计算的初始条件为

(www.xing528.com)

图1.19　电子发射示意

在计算数学中,常微分方程的数值求解方法很多,各有特点,这些方法都可以用来求解电子运动方程。在电子光学问题中,目前流行的是使用方法稳定、普适性强且能较好达到精度要求的龙格—库塔法(Runge—Kutta)来求解电子运动方程[20]。计算二阶常微分方程的数值公式为

其中,

为了从轨迹的第n点(zn,rn)推算出下一点(zn+1,rn+1),应由式(1.36)求出k1、k2、k3和k4,然后代入式(1.34)和(1.35)即可。可见,计算轨迹的关键是精确地求出4个k值。下面简述其步骤。

计算k1:首先用插值的方法求V*(zn,rn),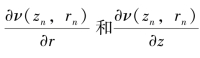,然后用zn,rn和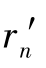作自变量解出式(1.34)等式右侧的函数,简称右函数。

计算k2:修改自变量,新的自变量为

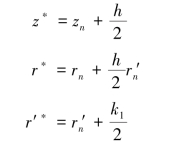
计算k3:首先修改自变量,新的自变量为

代入式(1.34)求出右函数,乘以h就得到k2。

计算k4:修改后新的自变量为

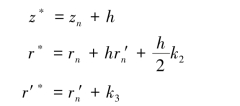
同样代入公式(1.34)求出与其对应的右函数,乘以h就得到k4。

这样由式(1.36)代入式(1.34)和(1.35)就可得到z=(n+1)h点的解。然后以zn+1、rn+1和作自变量用同样的步骤计算下一点的k1、k2、k3和k4,从而求出z=(n+2)h的解,如此往复,直至求得最后一点的电位值。

当用轨迹微分方程进行电子轨迹的追踪计算时,无论是近轴方程,或是实际轨迹方程,在阴极面附近都存在着奇异性。为了解决此问题,通常用近似方法求出第一点,以此为起点,用龙格—库塔法计算推进。

龙格—库塔法由起始点可推算出下一点,并依序推进。但由(1.32)可看出,在r″(z)的表达式中,分母存在V*(z)=V(z)+ε,当z=0时,V*(0)=ε,是个很小的量,对像增强器而言,所有阴极上的点都处在奇异的邻域内,不能求出r″,因此不能求出第一点。

注意:对电子枪而言是否存在奇异性应由具体结构及供电情况而定,在尚未清楚的情况下,暂且按存在处理。

为了解决此问题,通常用近似方法求出第一点,以此为起点,用龙格—库塔法计算推进。

计算第一点的近似方法:假定第一点与阴极发射电子处的距离足够近,认为在此范围是均匀场,轨迹呈抛物线形式;而在离轴远些的区域,考虑到非均匀场的影响,对轨迹作了适当的修正(体现在下式中的V″(z)),式为

式(1.37)和(1.38)中z只限于由阴极至第一点的区间,如图1.20所示。

图1.20　起点计算示意

在求解轨迹方程时,轨迹在每一步的落点往往不在网格节点上,为此通常采用拉格朗日插值法依据网格节点的电位值求得轨迹落点电位值及偏导数。

用拉格朗日九点插值公式计算电位的公式为

其中,

由(1.39)分别对r、z求导得到各项偏导数为

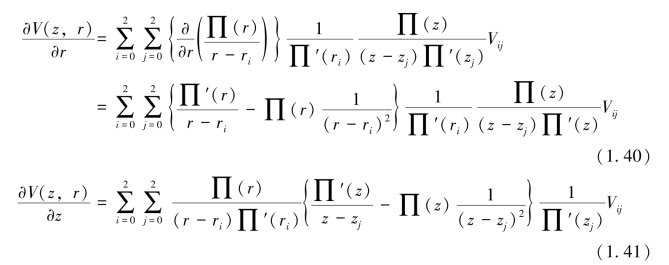
由式(1.39)(1.40)及(1.41),依据网格节点电位可求得非节点的任一点(z,r)的电位及偏导数,如图1.21所示。

图1.21　依据网格节点电位求非节点的任一点的电位及偏导数

4.电子轨迹的计算结果

热电子面发射源是轴对称结构,横坐标为热电子面发射源直径向距离,单位为mm,纵坐标为热电子面发射源轴向距离,单位为mm。计算结果如图1.22、1.23、1.24所示。

电子轨迹计算:起点电子初能量取0.1 eV,热电子发射角度取-90°～+90°,每增加5°计算一个轨迹,散射网的直径为30mm,图中坐标(-15～+15)mm,每隔1mm算一个发射点,假设电子均匀,由于盘状螺旋灯丝源半径为2.5 mm,所以在直径为5mm的范围,采用每隔0.5mm算一个发射点计算。

图1.22对应图1.16的电场分布——第一阳极电压值为-4 000 V,第二阳极电压值为0 V,左边图1.22(a)为电子轨迹分布,横坐标为热电子面发射源直径,单位为mm;纵坐标为热电子面发射源高度,单位为mm。右边图1.22(b)为荧光屏接收面直径方向分布的电子统计图,横坐标为热电子面发射源直径,单位为mm;纵坐标为电子数,平均值为35.877 677,荧光屏的发光直径是12 mm,热电子具有发散特性。

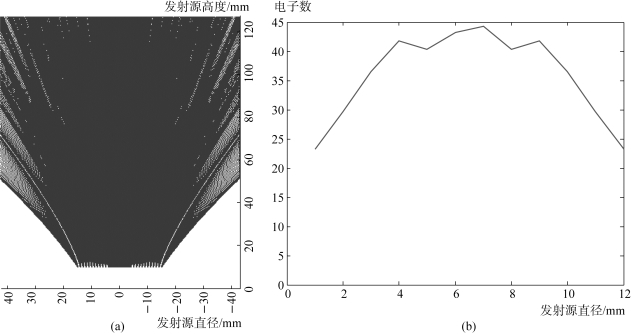
图1.22　热电子面发射源发散时电子轨迹和数量分布图

(a)电子轨迹分布;(b)电子数量分布

图1.23对应图1.17的电场分布——第一阳极电压值为-4 000 V,第二阳极电压值为-2 000 V,左边图1.23(a)为电子轨迹分布,横坐标为热电子面发射源直径,单位为mm;纵坐标为热电子面发射源高度,单位为mm。右边图1.23(b)为荧光屏接收面直径方向分布的电子统计图,横坐标为热电子面发射源直径,单位为mm;纵坐标为电子数,平均值为24.787 540,荧光屏的发光直径是12 mm,热电子具有均匀特性。

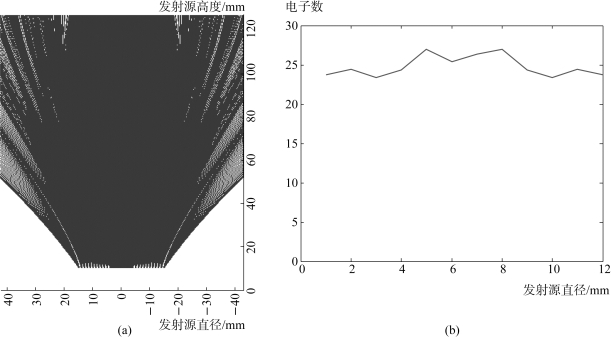
图1.23　热电子面发射源均匀时电子轨迹和数量分布图

(a)电子轨迹分布;(b)电子数量分布

图1.24对应图1.18的电场分布——第一阳极电压值为-4 000 V,第二阳极电压值为-3 990 V,左边图1.24(a)为电子轨迹分布,横坐标为热电子面发射源直径,单位为mm;纵坐标为热电子面发射源高度,单位为mm。右边图1.24(b)为荧光屏接收面直径方向分布的电子统计图,横坐标为热电子面发射源直径,单位为mm;纵坐标为电子数,平均值为74.346 028,荧光屏的发光半径是6mm,中心亮斑半径是3.088 154 mm,热电子具有汇聚特性。

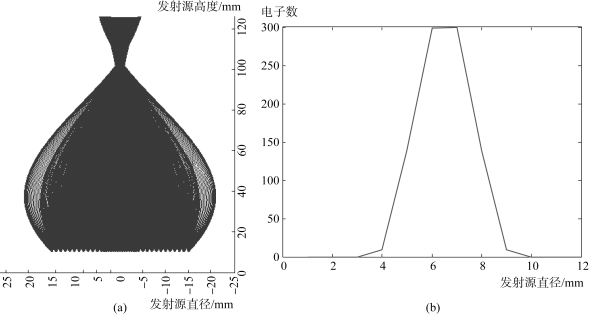
图1.24　热电子面发射源汇聚时电子轨迹和数量分布图

(a)电子轨迹分布;(b)电子数量分布

总之,在固定第一阳极电压为-4000V后,分别计算第二阳极电压为0V、-1000 V、-1 200 V、-1 500 V、-2 000 V和-3 990 V的电子轨迹以及荧光屏接收电子的分布数量,并将接收电子数量在荧光屏直径上的分布绘制成图1.25,图的横坐标为荧光屏接收面直径,单位mm,纵坐标为直径方向电子数,图右上角中b为第二阳极电压。

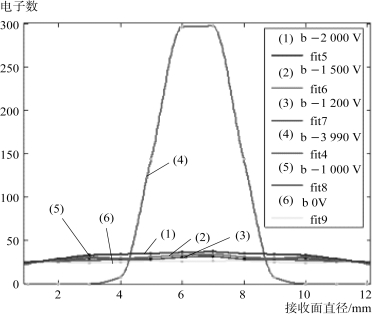
图1.25　不同电压下荧光屏接收面直径方向的电子分布图

从图中可以看出第二阳极电压在-2 000～0 V时,电子分布变化不大,-2 000 V时最好;第二阳极电压在-2 300～-4 000 V时,电子分布开始汇聚,-3 990 V时汇聚成点,中心亮斑半径是1.686 412mm,如图1.26所示。

第二阳极电压由-3 990 V(荧光屏亮)增加到-4 010 V(荧光屏不亮)是一个瞬间过程,激发电子淹没在第二阳极桶内,满足荧光屏余辉测试时瞬间截断激发电子轰击荧光屏的要求,称为电子的淹没特性。

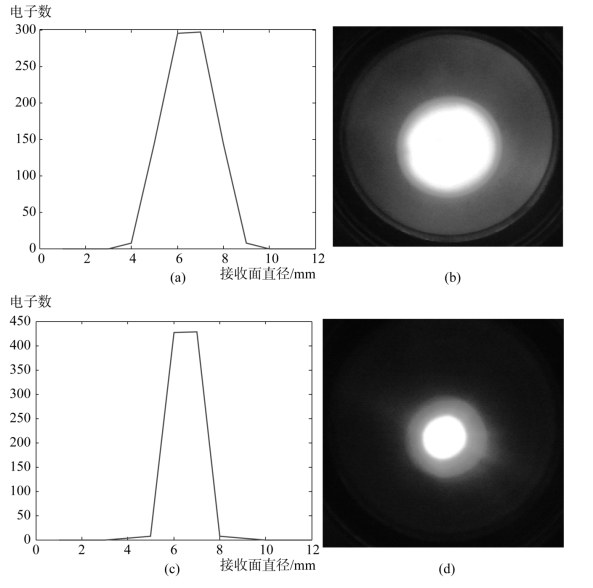
图1.26　荧光屏接收面直径方向的电子分布及数码照片

(a)第二阳极电压为3 990 V的电子分布图;(b)第二阳极电压为3 990 V的数码照片;(c)第二阳极电压为4 010 V的电子分布图;(d)第二阳极电压为4 010 V的数码照片