热电子面发射源的理论分析

1.真空系统中电子发射特性

在真空系统(1×10-5 Pa)中,钽丝与钨丝电子发射特性基本相同,钽丝在常温下便于弯曲,不易氧化,钨丝在常温下刚度较高,不易弯曲,如果用钨丝做造型则需要高温,但高温容易氧化,必须在真空环境下做造型,所以选用在常温下具有更好的稳定性和可塑性的钽丝做电子发射源。现分析钽丝的电流发射密度J0与温度T的关系,在0电位电场时,其理论热电子发射公式为[1]

式(1.1)中:A0为发射常数的理论值,钽丝为55 A/(cm2·K2);φm为所用金属的逸出功,钽丝的φm=4.19 eV;k为玻耳兹曼常数(1.380 649×10-23 J·K-1)。

钽丝在1 600～2 000 K时才有热电子发射,综合考虑灯丝温度和电源的功率,经过试验,φ0.3mm的灯丝比较合适,在这个温度范围,钽丝的电流发射密度与温度的关系如图1.1所示,温度对钽丝的热电子发射有非常大的影响,因此有必要对热电子发射源进行热平衡分析。

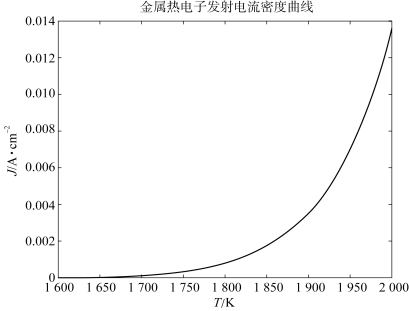
图1.1　钽丝热电子发射电流密度与温度关系曲线

2.热电子面发射源造型理论模型的建立

为了进一步分析荷兰DEP公司的电子发射源,现建立3种造型的电子发射源数学模型。近似条件假设:灯丝初始状态温度相同。灯丝的热传导需要时间,假如灯丝初始状态等温,那么只要灯丝各点接收到的热辐射能量相等,由于灯丝吸收热辐射系数不变(取决于它的材料),灯丝各处温度就相同,也就不用考虑热传导对灯丝温度的影响。所以在初始温度相同的前提下,我们分析热辐射的均匀性。现在考虑在直径为D=8mm的面积上分布4圈螺旋灯线,分别建立3种灯丝的热辐射方程,同时把螺旋灯丝假设为间隔相同的4个同心圆,因不考虑热传导就假设灯丝是不相通的同心圆,因为是圆周对称的,所以不妨就以横截面上的一个点来建立数学模型,以便简化计算。灯丝材料为钽丝,辐射能量为Ea,吸收能量为Eb[2]。

钽丝在1 600～2 000 K的温度下,全法向平均有效发射率为ε=0.213,全波长吸收平均系数为α=0.438。

灯丝是均匀的细圆柱钽丝,体积设为V=S·L,S(mm2)是灯丝的横截面面积,L(mm)为灯丝的长度,La为计算A点热平衡处的灯丝长度,Lb为对A点有热辐射的灯丝长度,灯丝螺旋线水平距离为,斯忒藩-玻耳兹曼常数σ=5.670 32×10-8(W·m-2·K-4),灯丝温度为T(K)。

E1、E2、E3、E4分别为灯丝每圈的热量增量的平均值。L1、L2、L3、L4为灯丝每圈的周长,H为灯丝的间距取1mm。灯丝单位长度的热增量公式为

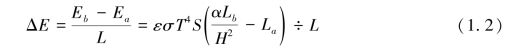
热增量单位为J/mm,令Q=εσT4 S则建立下面的方程。

(1)平面螺旋灯丝。

灯丝的平面和纵断面如图1.2所示,在电子发射源直径D=8 mm的条件下,由式(1.2)推导灯丝每圈热量增量公式。

图1.2　平面螺旋灯丝的平面和纵断面图

(a)平面图;(b)纵断面图

对于圈1,它的热量增量为它吸收圈1、圈2的热辐射能量减去它向外辐射的能量,由图示圈1断面两点距离为2H,所以公式中第一项系数为(2H)2,具体见式(1.3);推导圈2时,对它有辐射的是1和3,4被3挡住所以不考虑;推导圈3时,对它有辐射的是2和4;推导圈4时,对它有辐射的是3;灯丝每圈的平均热量增量方程为

(2)锥形螺旋灯丝。

如图1.3所示,θ为圆锥角,H11、H12、H13、H14、H22、H23、H24、H33、H34、H44分别为灯丝间的径向距离,计算条件底圆直径为8 mm。由式(1.2)推导时,图中标1的圈的能量增量为1、2、3、4圈对它的辐射能量之和减去1圈向外辐射的能量;其他每圈类似推导。灯丝每圈的平均热量增量方程为

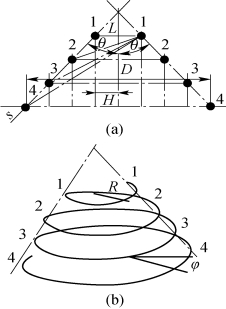
图1.3　锥形螺旋灯丝的平面和纵断面图

(a)平面图;(b)纵断面图

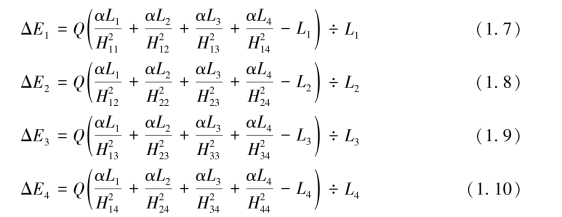
分别计算θ=30°、45°、60°时的热量增量的平均数据。

(3)半球形灯丝。

假设螺旋灯丝横断面均匀分布在直径为8mm的半圆上,θ为灯丝间的圆心角,θ=22.5°,如图1.4所示。H11、H12、H13、H14、H22、H23、H24、H33、H34、H44分别为灯丝间的弦长。由式(1.2)推导时,图中标1的圈的能量增量为1、2、3、4圈对它的辐射能量之和减去1圈向外辐射的能量;其他每圈类似推导。灯丝每圈的平均热量增量方程为

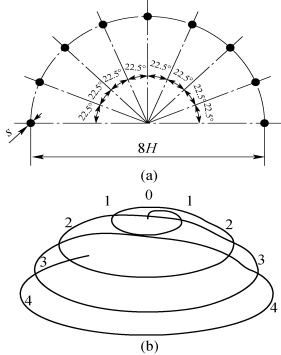
图1.4　半球形灯丝的平面和纵断面图

(a)平面图;(b)纵断面图

3.电子发射热平衡分析

通过编程计算式(1.3)(1.4)(1.5)(1.6)(1.7)(1.8)(1.9)(1.10)(1.11)(1.12)(1.13)(1.14),其典型数据如表1.1所示,其热量增量变化曲线如图1.5所示,图中纵坐标E表示灯丝每点能量的增加值,单位为J,横坐标D表示荧光屏直径,单位为mm,点划线表示荧光屏中心位置。

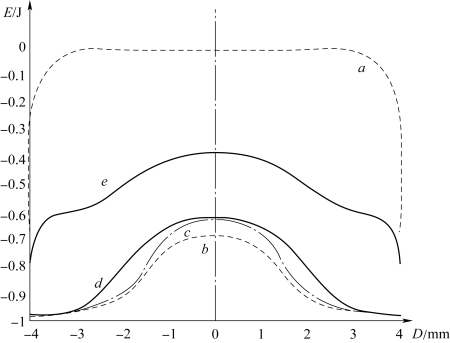
图1.5　3种灯丝的热量增量变化曲线(www.xing528.com)

a—平面螺旋灯丝;b—30°锥形螺旋灯丝;c—45°锥形螺旋灯丝;d—60°锥形螺旋灯丝;e—半球形灯丝。

表1.1　典型数据表　单位:J

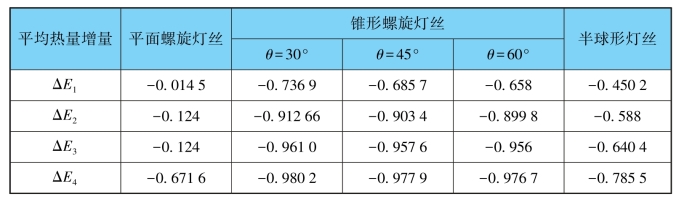
通过真空热辐射分析设计3种灯丝模型,分别是平面螺旋灯丝、锥形螺旋灯丝和半球形灯丝,并计算和综合比较得出结论:根据数据和曲线形状可以看到平面螺旋灯丝边界变化较大,但是中间温度非常平均,所以表面均匀性最好;半球形灯丝总体均匀性较好;锥形螺旋灯丝热发射的均匀性不太合理[3]。

4.电子发射源的热电子均匀性分析

下面分析前两种热电子发射源的热电子均匀性与造型的关系[4～5]。

(1)平面螺旋灯丝的热电子均匀性。如图1.6所示,平面螺旋灯丝单圈长度Lφ为

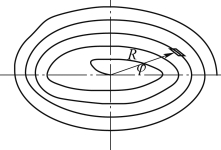
图1.6　平面螺旋灯丝示意

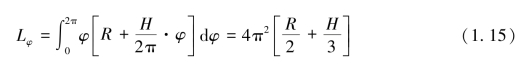
R的计算式为

R=r+(n-1)H

式中:r为内部第一圈圆的半径,n为圈数,H为灯丝每圈间距。

平面灯丝单圈的电子填充面积S(φ)为

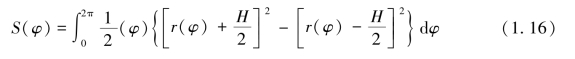
平面螺旋灯丝电子发射密度J S为

式中:d为灯丝直径,根据试验电流限制,取直径为0.3mm。

(2)锥形螺旋灯丝的热电子均匀性。如图1.3,R为圆锥底圆半径,R′为圆锥斜边长,θ为圆锥半锥角度,锥形螺旋灯丝长度L′(φ)为

锥形螺旋灯丝单圈的电子填充面积S(φ)为

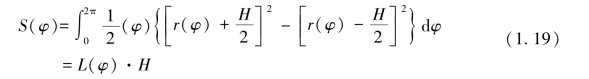
锥形螺旋灯丝电子发射密度J S为

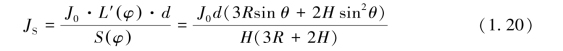
锥形螺旋灯丝每圈电子发射密度与锥角θ的关系如图1.7所示,图中1、2、3、4、5分别表示第1、2、3、4和第5圈灯丝电子发射密度与锥角θ的关系,第1圈是图中最下面的一条,依次类推;从图中看出灯丝电流密度汇交在θ=0 rad和θ=π/2两处,也就是说当θ=π/2时,灯丝的5圈电子发射密度相同;θ=0 rad是指灯丝成点发射源了,不存在密度计算;可以看出灯丝电子发射密度与锥角θ有关,当θ等于90°时,灯丝电子发射密度就是均匀的,进一步可以肯定最合理的灯丝为平面螺旋灯丝[6～14]。

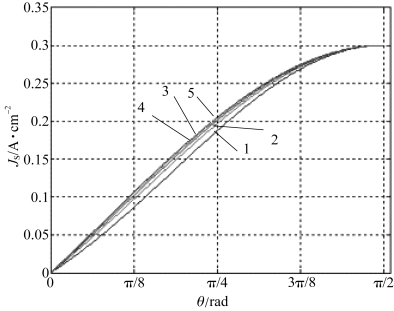
图1.7　电子发射密度与锥角θ的关系

5.实验结果及结论

在真空度为1×10-5 Pa的环境下,首先调节平面螺旋灯丝电流和电压,产生的热电子轰击荧光屏并使得其均匀性最佳;然后在同等条件下,试验了锥形螺旋灯丝和半球形灯丝,具体试验结果如图1.8和图1.9所示,采集图片顺序依次为1:平面螺旋灯丝、2:θ=75°锥形螺旋灯丝、3:半球形灯丝、4:θ=45°锥形螺旋灯丝,图1.9热电子轰击荧光屏发光图像的灰度Y值与直径X的关系曲线的1、2、3、4也是这个顺序。

图1.8　几种灯丝的热电子轰击荧光屏的图像

(a)1:平面螺旋灯丝;(b)2:θ=75°锥形螺旋灯丝;(c)3:半球形灯丝;(d)4:θ=45°锥形螺旋灯丝

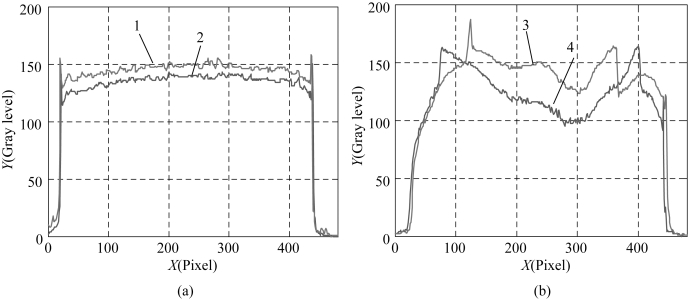
图1.9　热电子轰击荧光屏发光的图像的灰度Y值与直径X的关系曲线

(a)平面螺旋灯丝、θ=75°锥形螺旋灯丝;(b)半球形灯丝、θ=45°锥形螺旋灯丝

从图像以及其灰度曲线可以看出平面螺旋灯丝的均匀性最好,θ=75°锥形螺旋灯丝的均匀性与之接近,半球形灯丝的均匀性较差,θ=45°锥形螺旋灯丝的均匀性最差;进一步验证了下面的结论。

在真空系统中,热电子发射受温度的影响很大,通过对3种电子发射源造型的热平衡和热电子发射电流密度公式的推导、分析和实验验证,得出最合理的灯丝造型为平面螺旋灯丝。