11.1 根据实验测得的频率响应函数求出系统的模态参数(频率、模态向量、阻尼比)的过程称为实验模态分析。频率响应函数是根据输入和输出的关系来计算的,常用的方法有三种,现分述如下。
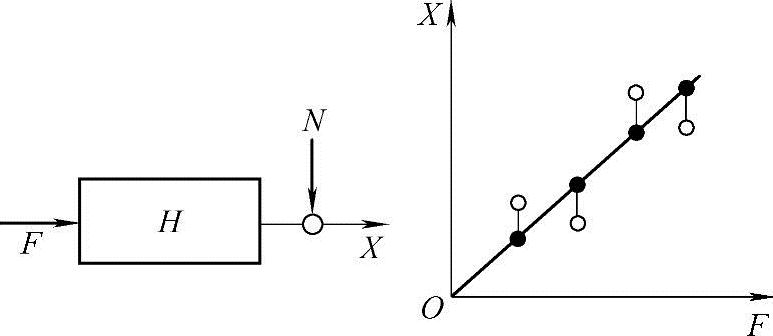
图11.1
(1)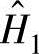 估计(设输出端有杂讯干扰,见图11.1):
估计(设输出端有杂讯干扰,见图11.1):
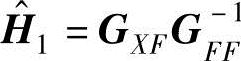
式中,GXF为输入和输出函数的互功率谱矩阵;GFF为输入函数的自功率谱矩阵。
 估计是一种欠估计,即
估计是一种欠估计,即 估计的频率响应函数值小于真实值。
估计的频率响应函数值小于真实值。
(2)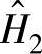 估计(设输入端有杂讯干扰,见图11.2):
估计(设输入端有杂讯干扰,见图11.2):

式中,GXF为输入和输出函数的互功率谱矩阵;GXX为输出函数的自功率谱矩阵。

图11.2
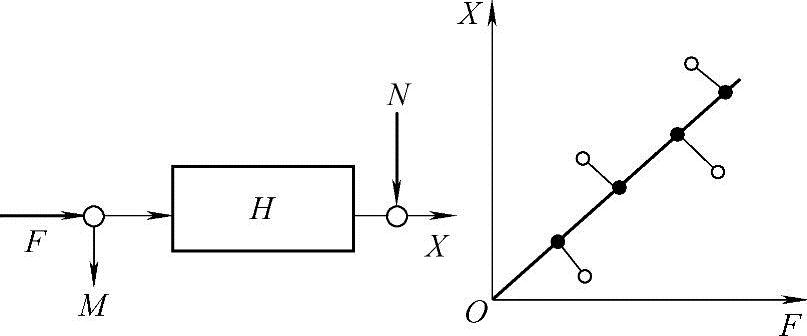
图11.3
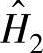 估计是一种过估计,即
估计是一种过估计,即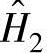 估计的频率响应函数值大于真实值。
估计的频率响应函数值大于真实值。
(3)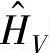 估计(设输入和输出端都有杂讯干扰,见图11.3):
估计(设输入和输出端都有杂讯干扰,见图11.3):
可以证明,频率响应函数矩阵可由如下矩阵的最小特征值所对应的特征向量求出:
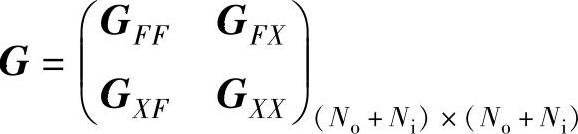
式中,No为输出自由度(即频率响应函数矩阵的行数);Ni为输入自由度(即频率响应函数矩阵的列数)。
 估计的频率响应函数界于
估计的频率响应函数界于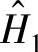 和
和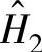 之间,是最好的估计。
之间,是最好的估计。
11.2 杂讯干扰对实测频率响应函数的影响可用相干函数来评估:
(1)常相干函数:
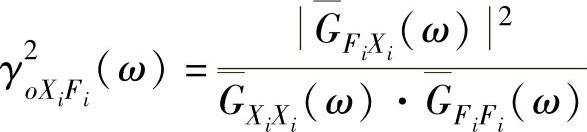
式中,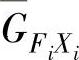 为输入和输出函数的互功率谱的平均值;
为输入和输出函数的互功率谱的平均值;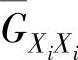 为输入函数的自功率谱的平均值。
为输入函数的自功率谱的平均值。
可以证明,常相干函数的值界于0和1之间。若其值接近1,说明输出完全是由输入引起的;若其值很小或接近于0,表明所测得的输出是由某种未被测量的输入引起的。
(2)多相干函数:

式中,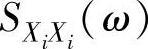 为输入函数的自功率谱;Snn(ω)为输出端杂讯干扰信号的自功率谱。
为输入函数的自功率谱;Snn(ω)为输出端杂讯干扰信号的自功率谱。
多相干函数的值界于0和1之间。若其值接近1,说明输出完全是由输入引起的;若其值很小或接近于0,表明所测得的输出是由某种未被测量的输入引起的。
(3)偏相干函数:
考虑信号X1,…,Xi,Xj,…。其中Xi和Xj之间的偏相干函数是在消去X1,…,Xg之后的相干函数,定义如下:
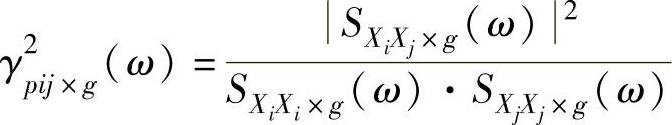
式中,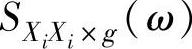 为Xi的自谱(不考虑X1,…,Xg的影响);
为Xi的自谱(不考虑X1,…,Xg的影响);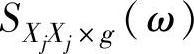 为Xj 的自谱(不考虑X1,…,Xg的影响);
为Xj 的自谱(不考虑X1,…,Xg的影响);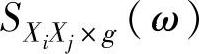 为Xi和Xj的互谱(不考虑X1,…,Xg的影响)。
为Xi和Xj的互谱(不考虑X1,…,Xg的影响)。
偏相干函数的值界于0和1之间。若其值接近1,说明所考虑的两个信号是相关的;否则是不相关的。
11.3 离散傅里叶变换(DFT)和快速傅里叶变换(FFT):

这些方程给出:①在N个离散频率点(mΔf)处的功率谱值SX(mΔf);②在N个离散时间点(nΔt)上的函数值x(nΔt)。
DFT将N个时域数据点转换成频域的N/2条谱线。FFT是进行DFT的快速算法,它要求数据点数N必须是2的整数次幂(如2,4,8,…,1024,2048等)。
以下关系成立。
采样时间间隔: Δt
频率分辨率: Δf
时间窗长度: 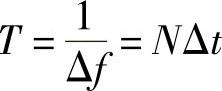
数据点数: 
最高频率: 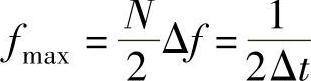
采样频率: 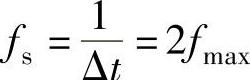
11.4 采样定理:为防止混迭,采样频率至少应等于所希望看到的最高频率的2倍。
11.5 实验模态分析的理论基础:频率响应函数矩阵和模态参数之间的关系可表示为
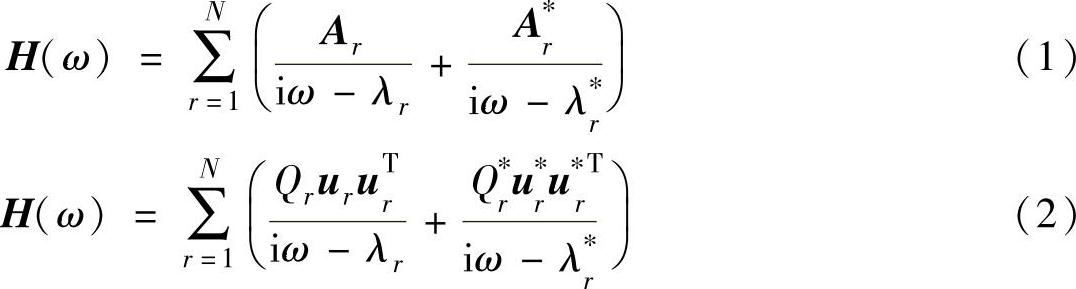
式中,λr=σr+iωr为系统的极点; ;σr为阻尼因子;ωr为有阻尼自然角频率;ω为角频率变量;Ar为模态r的留数矩阵;ur为模态向量;Qr为模态因子;∗为复共轭;N为模态数。
;σr为阻尼因子;ωr为有阻尼自然角频率;ω为角频率变量;Ar为模态r的留数矩阵;ur为模态向量;Qr为模态因子;∗为复共轭;N为模态数。
上式左边由实验测得,模态参数可通过求解式(2)而得到。方法是,先在时域里求系统的极点,再在频域中求模态向量。
11.6 模态参数估计的各种方法:由频率响应函数(FRF)矩阵求模态参数的方法有多种,但这些方法都能以自回归移动平均模型(简称ARMA)为出发点而导出。为此,首先将FRF矩阵通过逆傅里叶变换变成时域里的冲击响应函数(IRF)矩阵,再以各种方法求解。现分述如下。
(1)复指数法(Complex Exponential Algorithm,CEA) 用IRF矩阵的一个元素h的采样值构成ARMA模型:

式中,h(i)=h(i·Δt)为h的第i个采样值。
在以上分析中,对时间起点并无任何限制,我们可用h(1),h(2),…作为新的h(0),h(1),…建立ARMA模型,从而得到2N个方程:
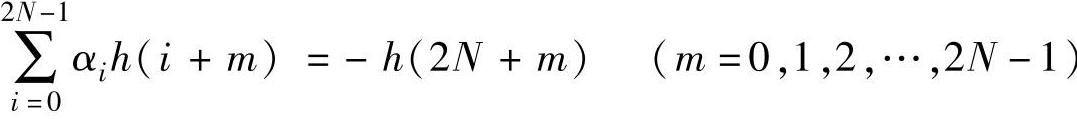
此处m表示时间延迟指标。写成矩阵形式为
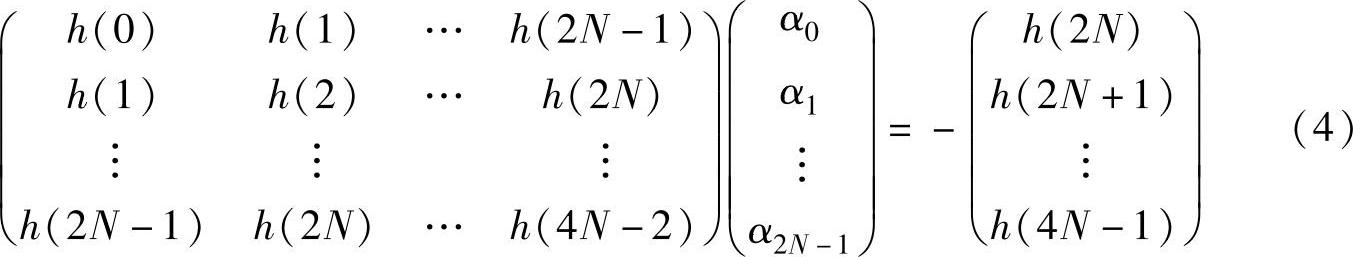
或

式中,h为陶布李兹(Toeplitz)矩阵。
由此解得

求出系数αi后,再求解下面的特征方程
α0+α1z1+…+z2N=0 (7)
求得特征值zr后,即可按下式求阻尼和角频率:
阻尼因子:  (https://www.xing528.com)
(https://www.xing528.com)
阻尼比: 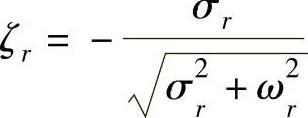
有阻尼自然角频率: 
(2)最小平方复指数法(Least-Squares Complex Exponential,LSCE) 用复指数法建立ARMA模型,使方程数目多于2N,即

或
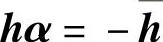
式中,矩阵h不是方阵。
ARMA系数由下式给出:

式中,h+是h的广义逆矩阵。求出系数αi后,特征根zr可按式(7)求得。
(3)多参考点时域法(Polyreference Time Domain,PTD) 用整个IRF矩阵的采样值构成ARMA模型,即

式中,

式中,n为矩阵列方向时间延迟次数;s为矩阵行方向时间延迟次数。
由此得ARMA系数矩阵:

式中,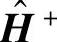 是
是 的广义逆矩阵。
的广义逆矩阵。
求出A后,特征根zr可通过解如下特征值问题而求得
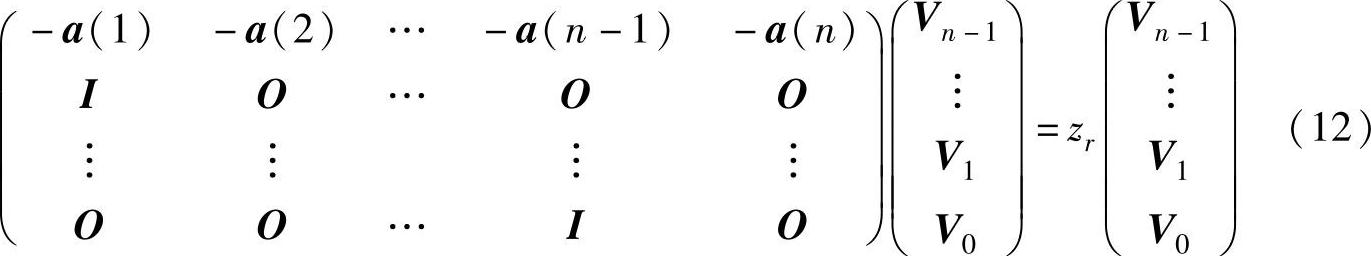
式中,a(n)(n=1,2,…)为方阵,其维数等于H矩阵的列数;I为和a(n)同维的单位矩阵;O为和a(n)同维的零矩阵;V0,V1等为和a(n)同维的列向量。
式(12)左边的第一个矩阵称为友矩阵。
(4)易布拉罕时域法(Ibrahim Time Domain,ITD) 用IRF矩阵的一列(例如,第q列)的采样值构成ARMA模型,即
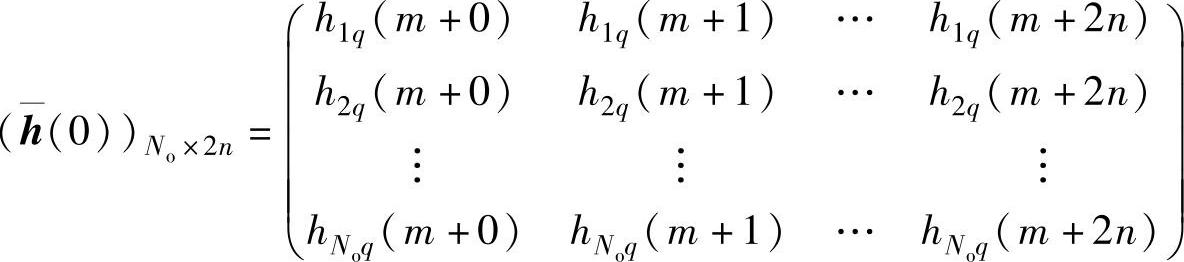

式中,No为输出自由度,即IRF矩阵的行数;n为要求的频率个数;q为输入自由度;m为时间延迟起点。
ARMA模型为
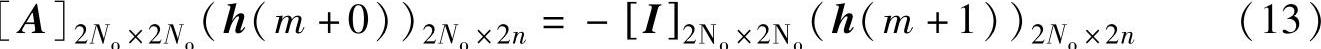
式中,
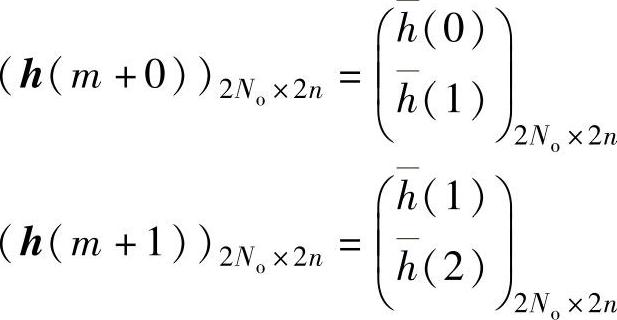
由此求得ARMA系数矩阵:
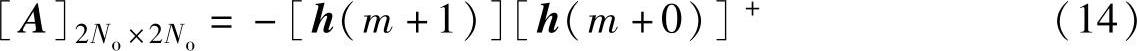
此处,[h(m+0)]+是[h(m+0)]的广义逆矩阵。
特征根可通过式(13)的Z-变换而求得。将z-1看成时间延迟算子,即在时域里延迟一步等于Z-域里乘以z-1。这样,由式(13)得特征值问题:
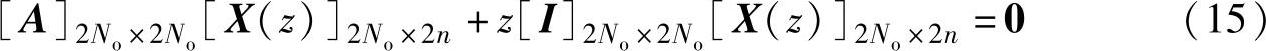
求得特征值zr后,即可按下式求阻尼和频率:
阻尼因子: 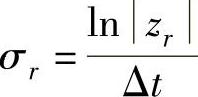
阻尼比: 
有阻尼自然角频率: 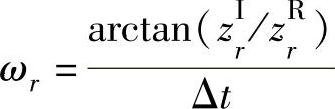
(5)特征系统实现算法(Eigensystem Realization Algorithm,ERA) IRF矩阵可表示为

式中, ;No为输出自由度,即IRF矩阵的行数;Ni为输入自由度,即IRF矩阵的列数;N为模态个数;
;No为输出自由度,即IRF矩阵的行数;Ni为输入自由度,即IRF矩阵的列数;N为模态个数;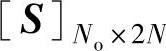 为模态矩阵;
为模态矩阵; 为模态参与矩阵。
为模态参与矩阵。
由[H(t)]的采样值构成广义汗克尔(Hankel)矩阵:
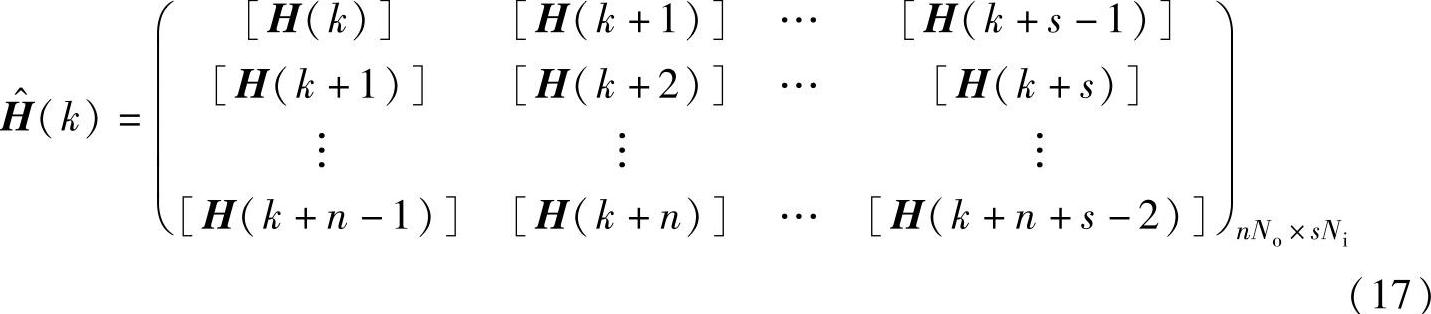
式中,[H(k)]=[H(kΔt)];Δt为采样周期;n为列方向的时间延迟数;s为行方向的时间延迟数。
注意,广义汗克尔矩阵可写成
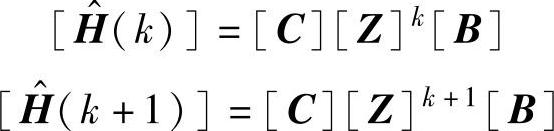
式中,

对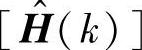 进行奇异值分解(SVD)得
进行奇异值分解(SVD)得
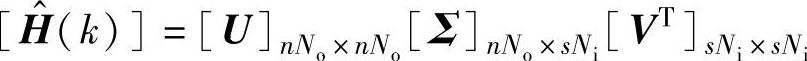
式中,[U]和[V]为正交矩阵;[Σ]为由奇异值构成的对角矩阵。
若非零奇异值的个数为m,则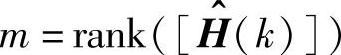 。令
。令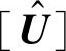 为
为 的前m列,则ARMA模型为
的前m列,则ARMA模型为
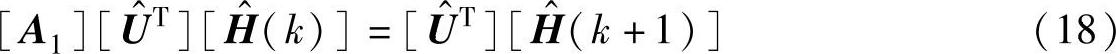
因为

由此得
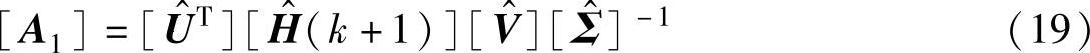
特征值问题为
[A1][ψ]=[ψ][Z] (20)
特征向量为

求得特征值zr后,即可按下式求阻尼和频率:
阻尼因子: 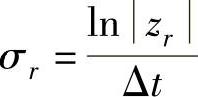
阻尼比: 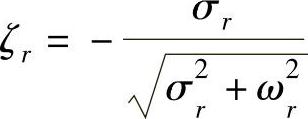
有阻尼自然角频率: 
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




