11.1 一单自由度系统的冲击响应函数的采样值如下：
h（0）=h（0·Δt）=0，h（1）=h（1·Δt）=1，h（2）=h（2·Δt）=0，h（3）=-1，Δt=1
用复指数法求系统的自然角频率和阻尼。
解：ARMA模型如下：
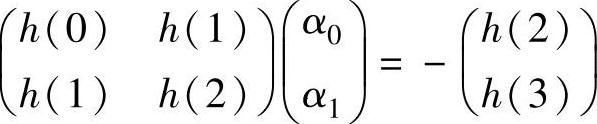
即
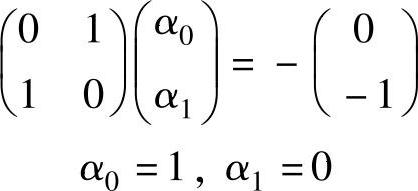
特征方程为
α0+α1z+z2=0
1+z2=0，z=±i
故阻尼因子和角频率分别为
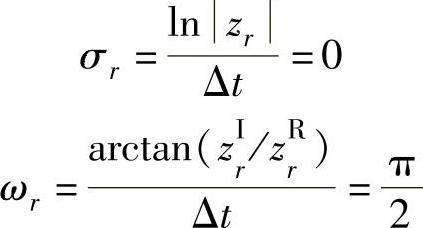
11.2 令系统的极点为λr=σr+iωr，证明：
模态质量：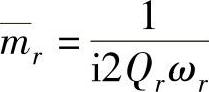 
，
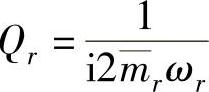
模态阻尼：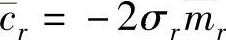 
模态刚度：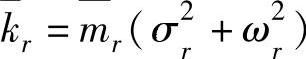 
证明：选取模态因子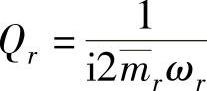
，则
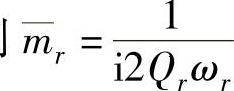。因
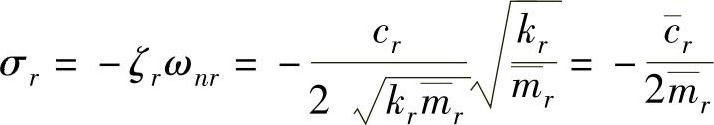
故模态阻尼可写成：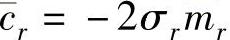
。最后，因
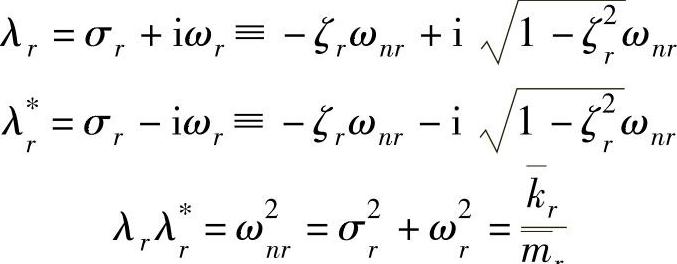
故模态刚度可写成：
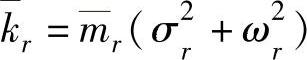
11.3 重复7.14题，按11.2题所示公式求：模态质量，模态阻尼和模态刚度。并证明，所得结果和用以下公式所得结果一致：STMS，STCS，STKS。
解：参考7.14题，系统的极点为
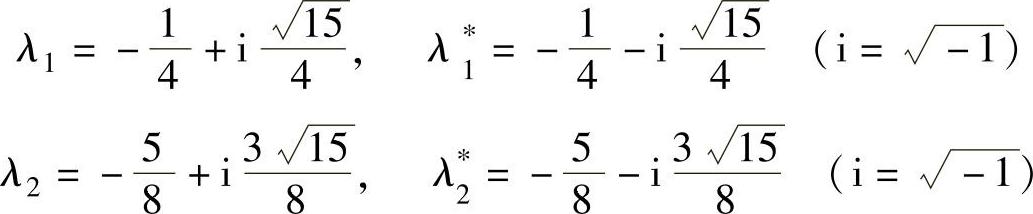
传递函数矩阵为
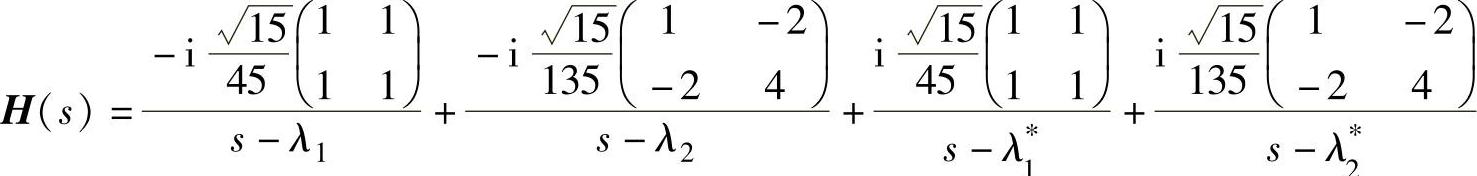
模态矩阵为
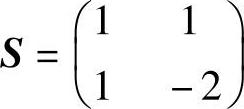
对应的模态因子为
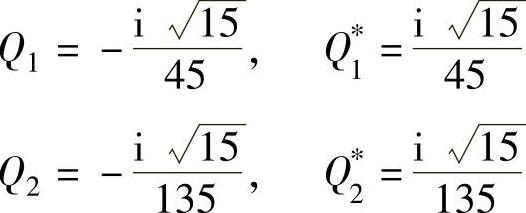
模态质量为
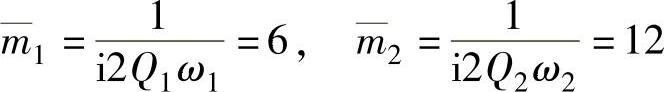
模态阻尼为
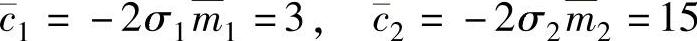
模态刚度为
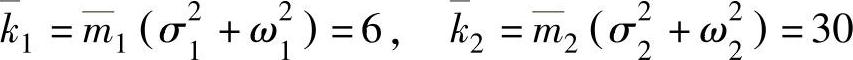
检验：质量矩阵，阻尼矩阵和刚度矩阵分别为
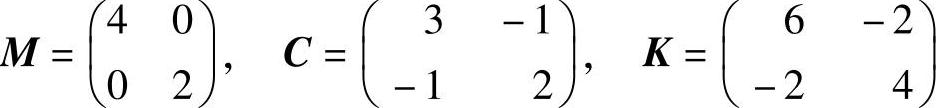
由此得
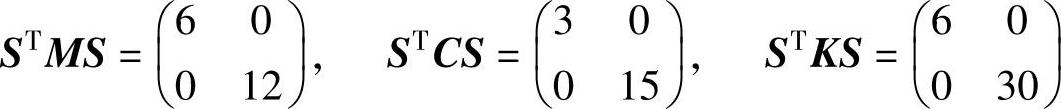
可见，所得结果和前面结果一致。
11.4 重复11.3题，选取模态因子使得相应的模态质量为1。
解：系统的极点为
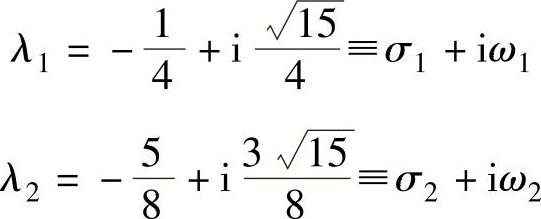
按11.2题所示公式，得模态因子：
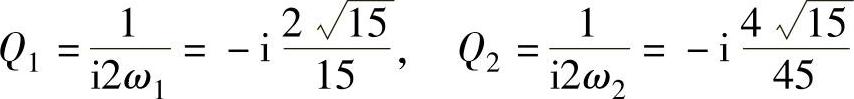
模态质量为
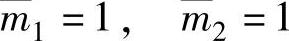
模态阻尼系数为
模态刚度为
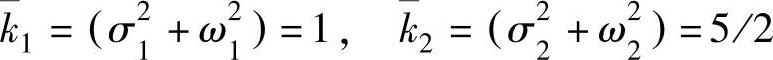
检验：未标准化的模态矩阵为
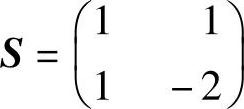
已知质量矩阵、阻尼矩阵和刚度矩阵为
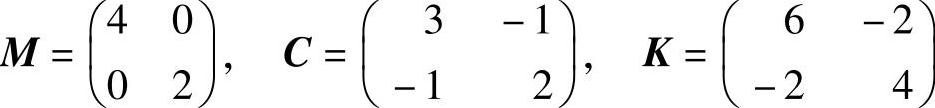
故
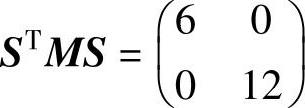
故标准化模态矩阵可写成
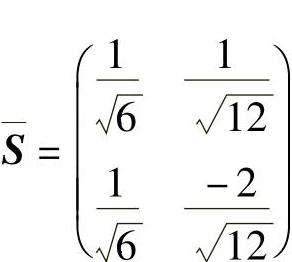
由此得模态阻尼系数和模态刚度：
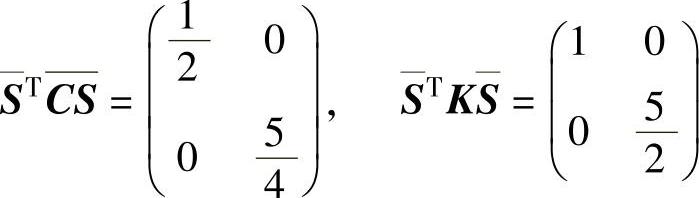
11.5 某系统如图11.4所示，其中m=10kg，c=20N·s/m，k=16000N/m。冲击响应函数的采样值列于表11.1中，求系统的极点，并和方程ms2+cs+k=0的根相比较。
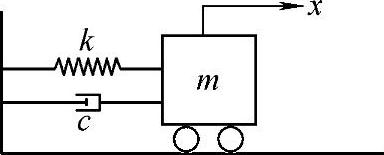
图11.4
表11.1 冲击响应函数的采样值
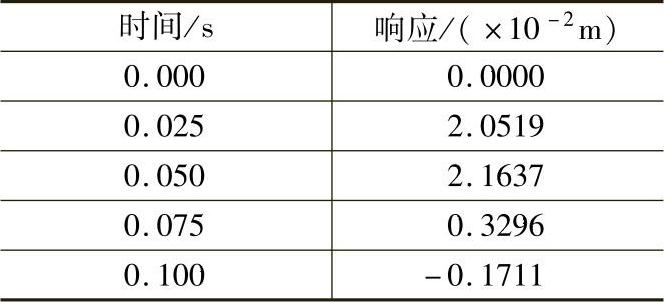
解：ARMA模型如下：
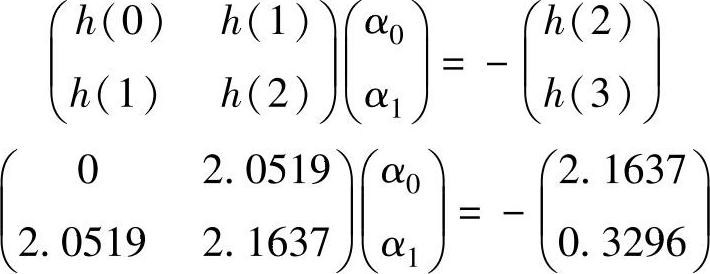
由此得
α0=0.9512，α1=-1.0544
特征方程为
α0z0+α1z+z2=0
由此得
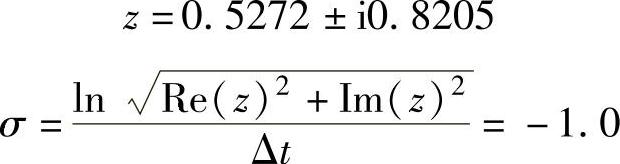
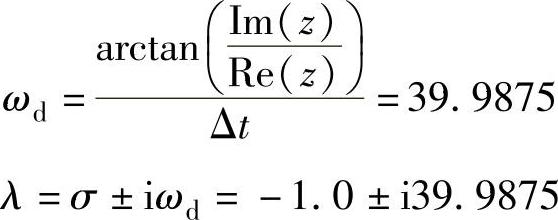
这和方程ms2+cs+k=0的根相同。
11.6 模态u1和u2之间的模态保证因子（Modal Assurance Criterion，MAC）定义如下：
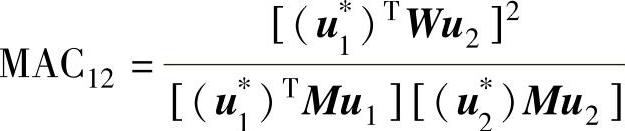
式中，W为加权矩阵；u∗1为u1的复共轭。
如果两模态是线性独立的，则MAC数为零，否则为1。试用7.14题的系统并用质量矩阵为加权矩阵求MAC11，MAC12和MAC22。
解：参考7.14题，有
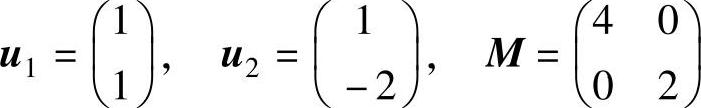
因此
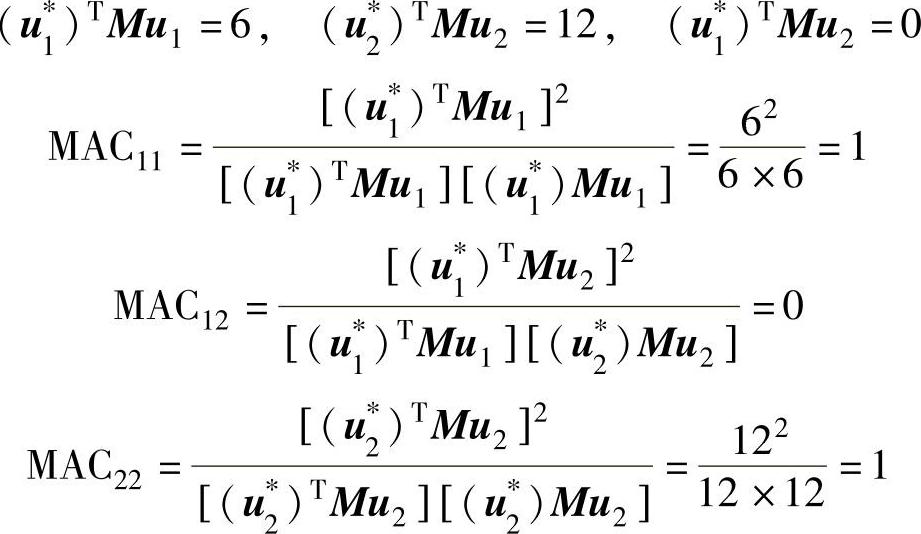
11.7 试用7.14题的系统证明：传递函数矩阵可写成：(https://www.xing528.com)
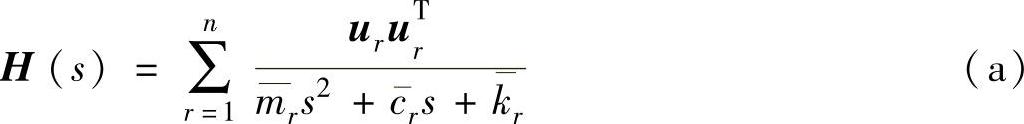
式中，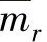
，
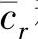和kr分别为模态质量、模态阻尼系数和模态刚度；ur为模态向量。
解：由7.14题知
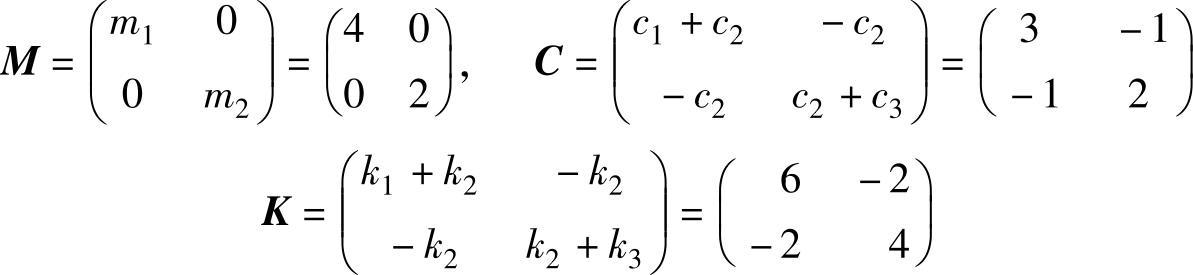
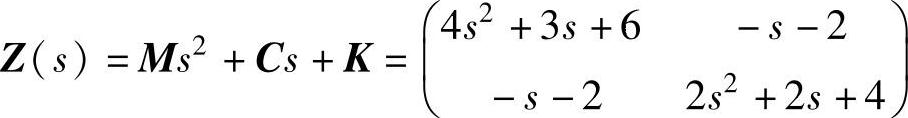
特征方程为|Z（s）|=0，即
8s4+14s2+33s2+20s+20=0
或
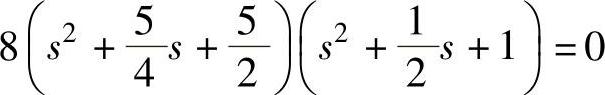
传递函数矩阵为
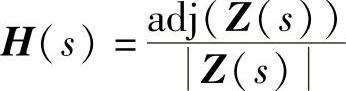
即
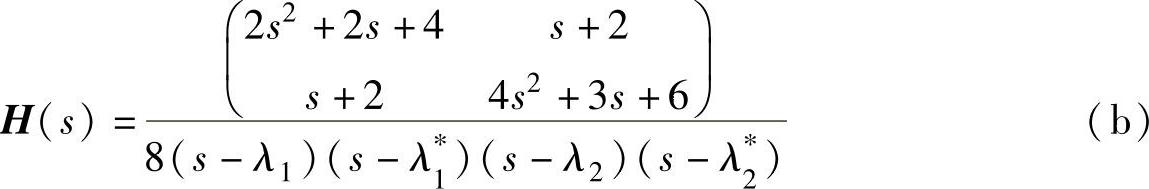
用留数矩阵的第一列求得模态矩阵为
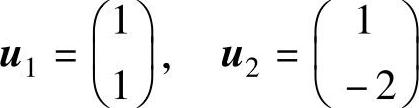
模态质量、模态阻尼系数和模态刚度如下（见11.3题）：
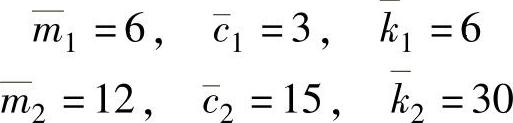
由式（a）得
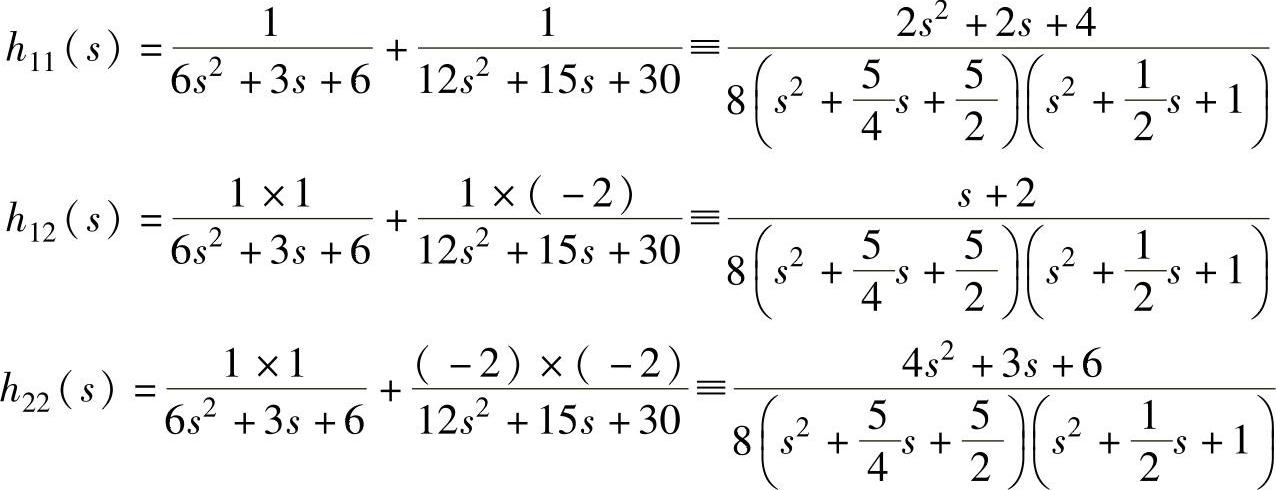
和式（b）相比较即知式（a）成立。
11.8 重复7.14题，求系统在时域里的响应。
解：由7.14题得
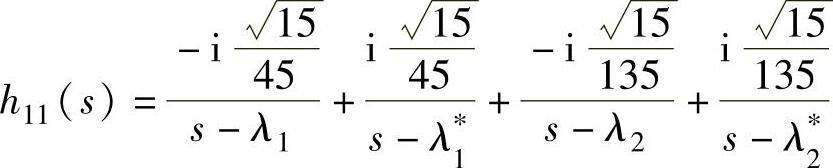
故
同理
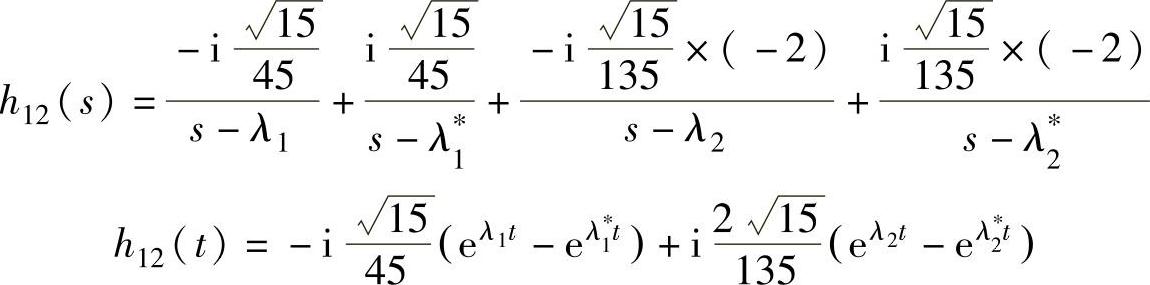
和
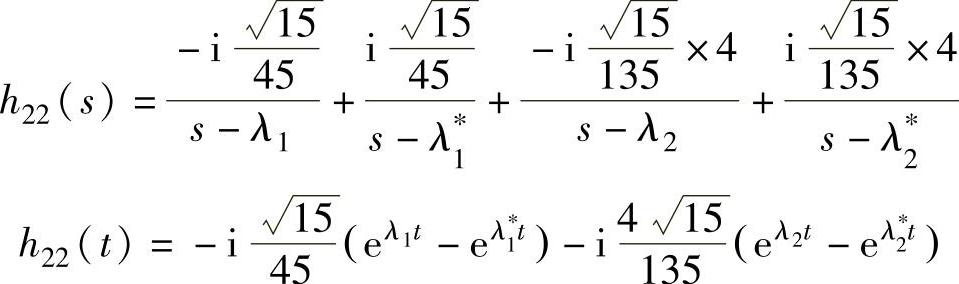
11.9 对某个二自由度系统，设“实验测得”的冲击响应函数矩阵如下所示，用CEA和PTD法求系统的模态参数。
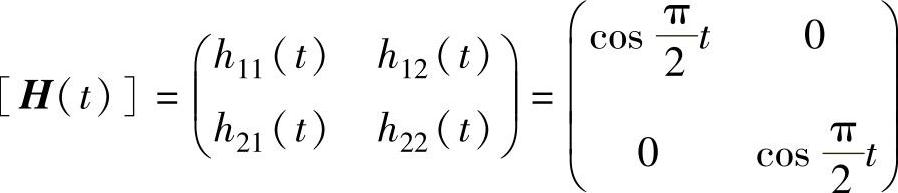
解：（1）CEA法：其基本思想是用冲击响应函数矩阵的一个元素构成AR-MA模型。我们取h11（t）和Δt=1，于是有
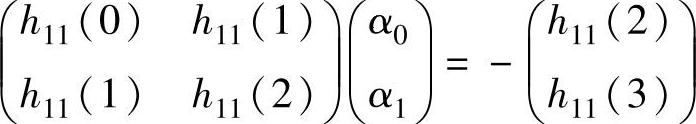
代入数值后，得
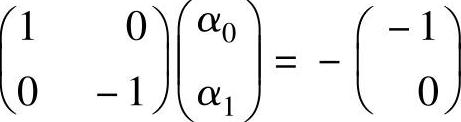
由此解得
α0=1，α1=0
特征方程为
α0z0+α1z1+z2=0
或
1+z2=0
由此解得特征根
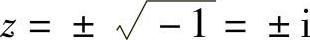
阻尼因子σ和自然角频率ω分别为
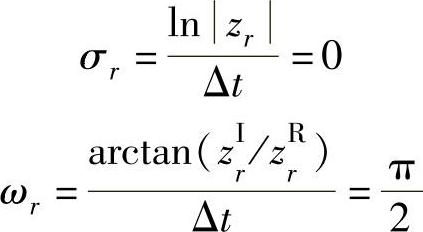
（2）PTD法：其方法是用整个冲击响应函数矩阵构成模型。取Δt=1，我们有
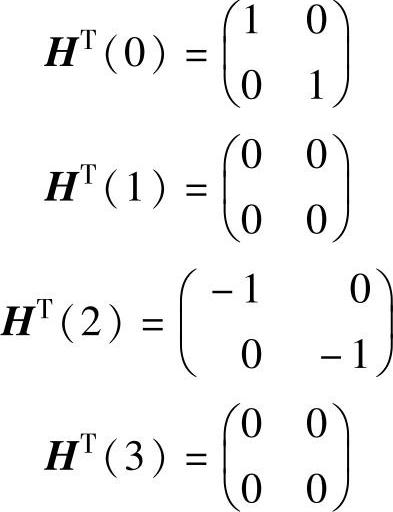
ARMA模型变为
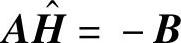
式中，
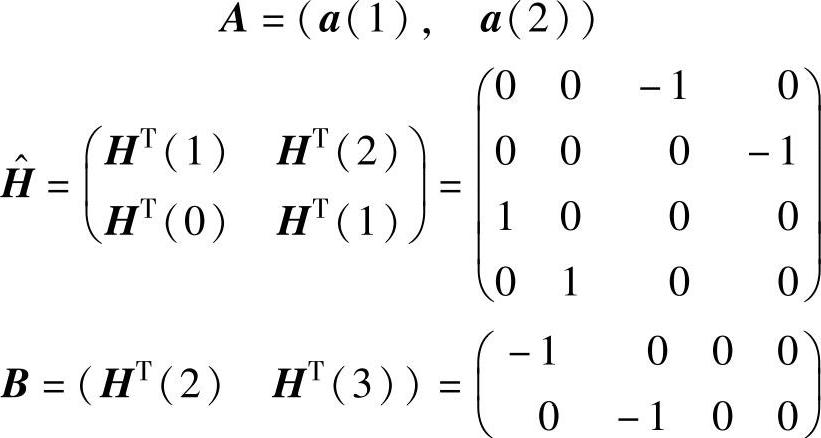
解得
a（1）=（O）2×2，a（2）=（I）2×2
相应的友矩阵为
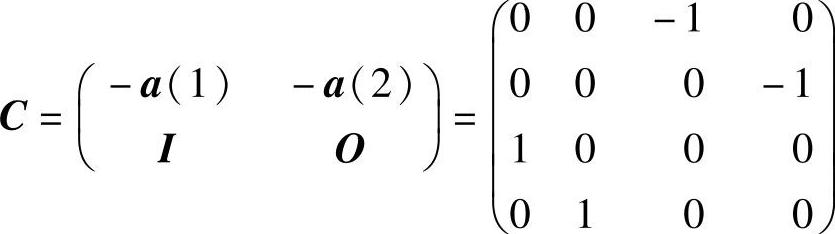
矩阵C的特征值为
z1，2=±i，z3，4=±i
由此可见，这和用CEA方法所得结果一致。
11.10 对某个二自由度系统，设“实验测得”的冲击响应函数矩阵如下所示，用ITD法求系统的模态参数。
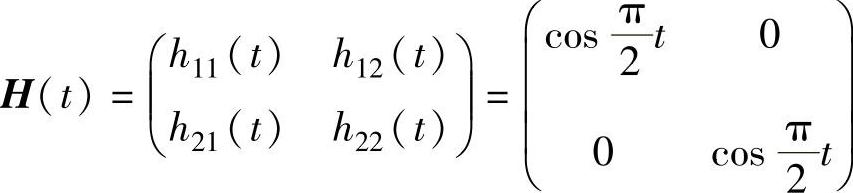
解：该方法是用冲击响应函数矩阵的一列构成ARMA模型。我们用第一列，并取m=0，n=2和Δt=1，于是有
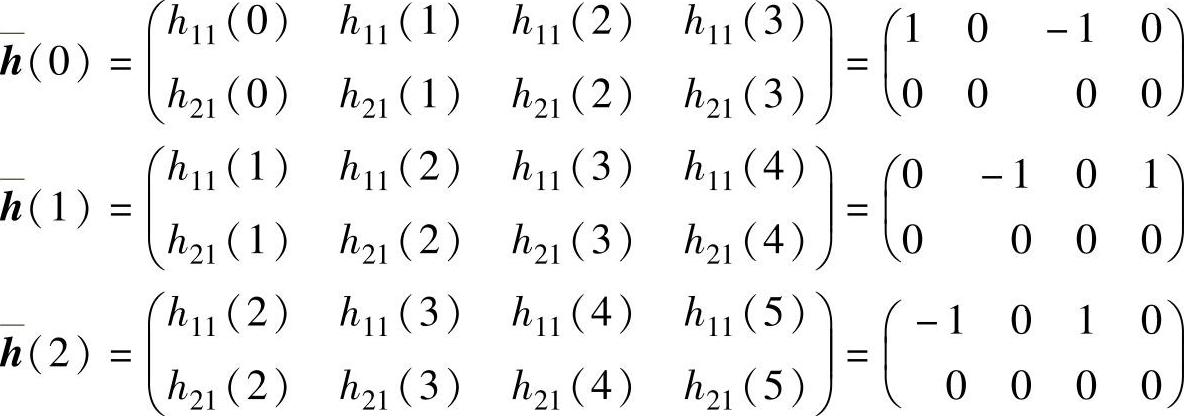
由此，得
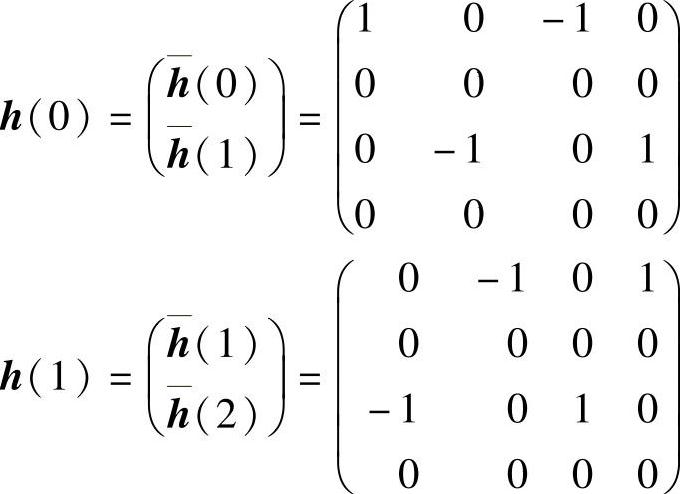
ARMA模型为
Ah（0）=-h（1）
由此解得矩阵A为
矩阵A的特征值为z1，2=±i和z3，4=0，故阻尼因子和自然角频率分别为
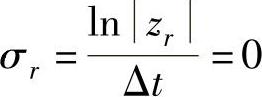
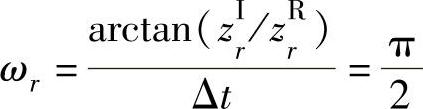
可见，这和用CEA和PTD方法所得结果一致。
11.11 对某个二自由度系统，设“实验测得”的冲击响应函数矩阵如下，用ERA法求系统的模态参数。
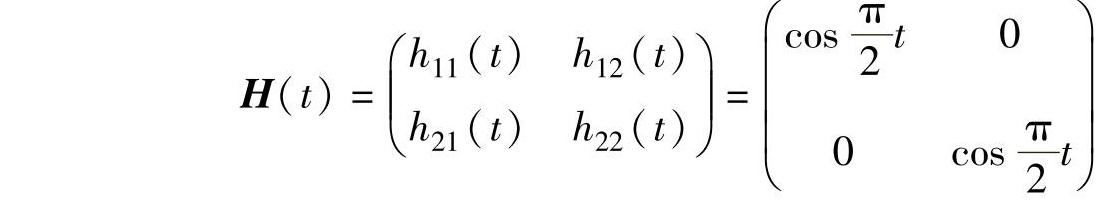
解：取Δt=1，先用整个响应函数矩阵构成广义汗克尔矩阵：
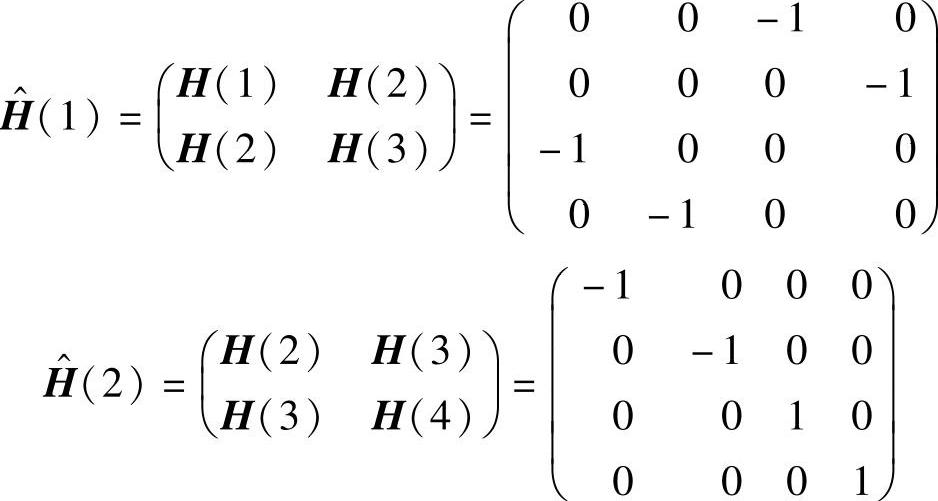
对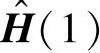
作奇异值分解（singular value decomposition，SVD），即
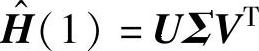
式中，U，Σ和V分别为
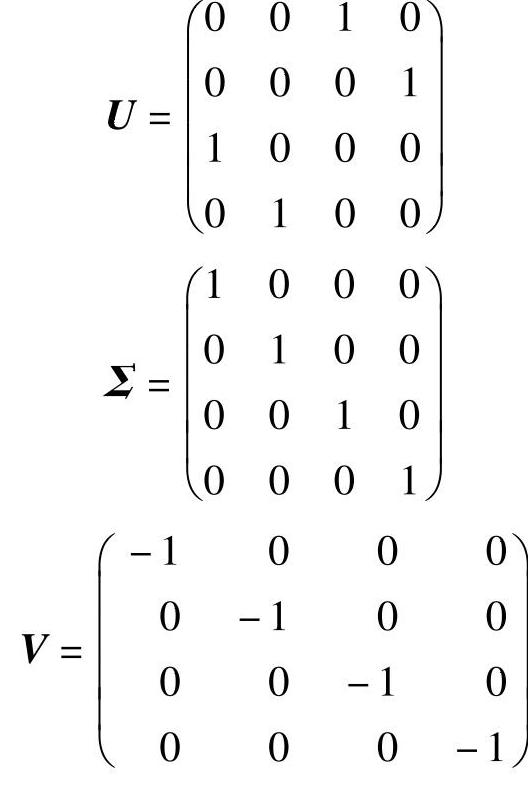
令矩阵A1为
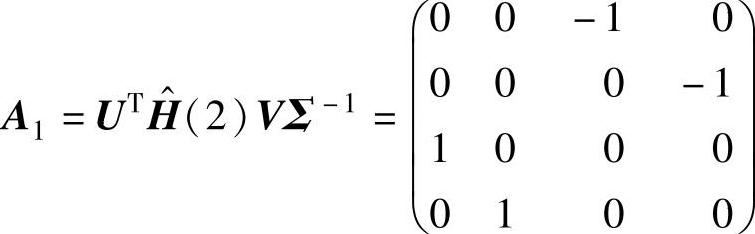
矩阵A1的特征值为z1，2=±i和z3，4=±i，故阻尼因子和自然角频率为
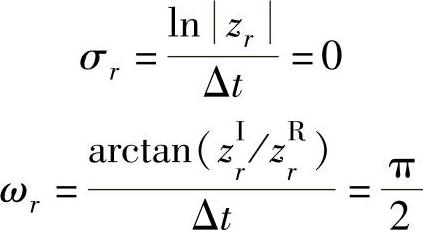
可见，这和用其他方法所得结果一致。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
