实验原理：求解q-τ关系下的K和qe，过滤实验操作技巧

广义地讲，过滤是借助于能将固体物截留而让流体通过的（过滤）多孔介质将固体物从液体或气体中分离出来的单元操作。工业上，过滤多指液固系统的分离。过滤过程的本质是流体通过固定颗粒层（滤饼）的流动，只不过在过滤过程中，固定颗粒层的厚度在不断增加，流体流动阻力也不断增大，因此，在推动力（压差）不变的情况下，单位时间内通过过滤介质的液体量也在不断减少。如果将单位时间内通过单位过滤面积的滤液量定义为过滤速率，即

式中　u——过滤速率，m/s；

V——通过过滤介质的滤液量，m3；

A——过滤面积，m2；

τ——过滤时间，s；

q——通过单位过滤面积的滤液量，m3/m2。

可以预测，在恒定压差下，过滤速率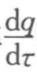和滤液量q与过滤时间有如图7-1所示的关系。

图7-1 过滤速率和滤液量与过滤时间的关系

尽管过滤是一个流体力学问题，但在过滤过程中，影响过滤速率的主要因素除了推动力（压差）大小、滤饼厚度外，尚有滤饼、悬浮液（含有固定颗粒的原料液）性质、悬浮液温度、过滤介质的阻力等诸多因素，因此，难以直接采用流体在圆管中流动的有关计算公式来计算过滤速率和阻力等问题。

如第1.2节中所阐述的那样，对于过滤问题，可以根据过程的本质和特征对实际过程做出适当简化，从而可以采用适当的数学方程（模型）进行描述。

比较过滤过程与流体通过固定床的流动可知，过滤速率即为流体经过固定床的表观速率u，同时，液体在细小颗粒构成的滤饼空隙中的流动属于低雷诺数范围。因此，可利用流体通过固定床压降的简化数学模型，寻求滤液量与时间的关系。

根据第1.2节的推导，在低雷诺数下，过滤速率可用康采尼（Kozeny）公式表示：

式中　K′——与滤饼空隙率、颗粒形状、排列方式等有关的常数，当Re′＜2时，K′＝5；

ε——滤饼的空隙率，m3/m3；

a——颗粒的比表面积，m2/m3；

Δp——压差，即过滤推动力，Pa；

μ——滤液黏度，Pa·s；

L——滤饼厚度，m。

根据物料衡算并考虑到过滤介质的阻力，可以导出过滤基本方程式：(www.xing528.com)

式中　γ——滤饼比阻，m﹣2，对可压缩滤饼，γ＝γ0（Δp）S，S称为压缩指数；

φ——悬浮液中的固含量，kg/m3清液；

μ——液体黏度，Pa·s；

qe——为形成与过滤介质阻力相当的滤饼层的虚拟滤液量。

为了简便起见，式（7-4）可改写为

或

式中的K、qe都称为过滤常数。

在恒压操作条件下，Δp为常数，对式（7-5）积分，可得

q2＋2qqe＝Kτ 　（7-8）

此即为恒压过滤方程。如若知道了K和qe，即可在过滤设备、过滤操作条件一定时，计算过滤一定的滤液量所需的操作时间；或者在过滤时间、过滤条件一定时，计算为完成一定生产任务所需的过滤设备（面积）的大小。通常前者称为操作计算，后者称为设计计算。

显然，只要做少量的实验，求得q-τ之间的关系，即可通过实验数据的处理得出K和qe。为此，将式（7-8）变换成如下形式：

实验时，只要保持过滤压力（差）不变，测得对应不同过滤时间所得到的滤液量，以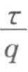对q在直角坐标系中作图，得一直线，读取直线斜率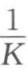和截距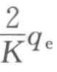，即可求得过滤常数K和qe，或者利用计算机直接对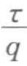和q的数据进行线性拟合，求得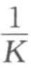和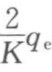，进而算得K和qe。

在组织实验时，由于过滤开始时刻在过滤介质上固体颗粒尚未形成滤饼，如若实验一开始即以恒压操作，部分颗粒就可能因在过滤推动力较大时穿过过滤介质而得不到清液。因此，在实验开始后，首先在较小压力下操作片刻，待固体颗粒在过滤介质上形成滤饼后，再在预定的压力下操作至结束。

如此，若在恒压过滤前的τ1时间内已通过了q1滤液量，则在τ1～τ和q1～q内将式（7-5）积分，整理后可得：

式（7-10）表明，q＋q1和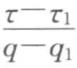为线性关系，采用与式（7-9）同样的处理方法，亦可方便地求得K和qe。

如果滤饼是可压缩的，则可在实验中改变过滤压力（差）△p，测得不同的K值，由K的定义式（7-7）两边取对数得

将K与△p在双对数坐标上标绘得一直线，直线的斜率为（1－S），由此可得滤饼的压缩指数S。将S代入式（7-11）可求出滤饼的比阻。

要说明的是，虽然△p是过滤的推动力，增大△p可使过滤速率增大，但过滤速率亦与过滤阻力有关。工业上，经常采用减小阻力的办法来强化过滤操作，例如采用性能良好的过滤介质，在原料悬浮液中添加硅藻土、活性炭等改善滤饼的结构，或加入其他有机的、无机的添加剂以减小悬浮液的黏度等措施，而这些也是过滤问题研究的重点内容。