函数误差的估计方法

在许多场合下，往往涉及间接测量的物理变量的误差估计问题。所谓间接测量的变量，就是本身不能直接被测量，但与其他直接可测的物理量之间存在着某种函数关系。由于直接可测变量的误差经过一系列函数运算，间接变量也产生了一定的误差，称为函数误差。显然，在直接变量与间接变量之间存在着误差传递过程。

3.5.1 函数误差的一般形式

设y＝f（x1，x2，⋯，xn），若自变量（即直接可测变量）x1，x2，⋯，xn的最大绝对误差分别为Δx1，Δx2，⋯，xn，按泰勒展开公式，函数y的最大绝对误差和最大相对误差分别为

其中称为误差传递函数。

由误差的基本性质和标准误差的定义，函数的标准误差为

3.5.2 某些函数误差的计算

（1）加法和减法

设y＝x1±x2±⋯±xn，且xi的标准误差为σi，则由式（3-10）和（3-12）得函数的最大误差为

函数的标准误差为

（2）乘法

设y＝x1，x2，⋯，xn，由式（3-11）得函数的最大相对误差：

（3）除法

设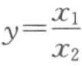，由式（3-11），得y的最大相对误差：

[例3] 若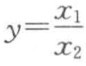，x1和x2的测量值分别为72.4和24.1，求y的最大相对误差和最大绝对误差。

解：由式（3-16）得，

（4）乘方或方根

设y＝xm，由式（3-12）得

（5）对数

设y＝lnx，由式（3-12）得

3.5.3 误差传递公式在间接测量中的应用

在实验研究过程中，对于间接变量的测定和误差分析，通常会遇到两类问题：一是当已知一组直接可测变量的误差后，计算间接变量的误差；二是预先规定间接变量的误差，计算各直接变量所允许的最大误差，从而为改进测定方式或选择适当的检测仪表提供依据。

[例4] 用量热器测定固体的比热容cp，可采用下式进行计算：

式中　M——量热器内水的质量，kg；

m——被测固体的质量，kg；

t0——测量前水的温度，℃；

T0——被测物体放入量热器前的温度，℃；

t2——测量时水的温度，℃；(www.xing528.com)

cp——被测固体的比热容，kJ/（kg·℃）；

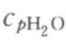——水的比热容，kJ/（kg·℃）。

测量结果如下：

M＝（250±0.2）g； m＝（62.31±0.02）g；

t0＝（13.52±0.01）℃；T0＝（99.32±0.04）℃；

t2＝（17.79±0.01）℃。

试求固体比热容的真值，并分析是否能提高测量精度。

解：先计算各直接变量的绝对误差和误差传递函数值。为方便计，令

t＝t2－t0＝4.27℃，T＝T0－t2＝81.53℃

则原方程可改写为

各变量的绝对误差为

ΔM＝0.2g；Δm＝0.02g，

Δt＝|△t2|＋|△t0|＝0.01＋0.01＝0.02（℃）

ΔT＝|△T0|＋|Δt2|＝0.04＋0.01＝0.05（℃）

各变量的误差传递函数为

函数的绝对误差：

Δcp＝8.41×10﹣4×0.2＋|﹣3.37×10﹣3×0.02 ＋4.92×10﹣2×0.02＋﹣2.58×10﹣3×0.05|＝1.3486×10﹣3≈1×10﹣3[J/（g·K）]

固体比热容的测量值为

固体比热容cp的真值为

cp＝（0.2101±0.001）J/（g·K）

如果要确定提高测量精度的可能性，须从分析各变量的相对误差方面考虑：

比较各变量的相对误差，现t的相对误差最大，是M的5.85倍，是m的14.63倍。显然，为了提高cp的测量精度，须改善t的测量精度，即提高测量水温的温度计精度。如采用贝克曼温度计，最小分度值为0.002℃，精度可达±0.001℃，t的相对测量误差变为

这样，在提高了t的测量精度后，各变量的测量精度就基本相当，cp的绝对测量误差为Δcp＝8.41×10﹣4×0.2＋|﹣3.37×10﹣3×0.02|＋4.92×10﹣2×0.002＋|﹣2.58×10﹣3×0.05|＝4.63×10﹣4≈5×10﹣4[J/（g·K）]

系统提高精度后，cp的真值为

cp＝（0.2101±5×10﹣4）J/（g·K）