建立与实际等效的数学模型及其在流体过滤中的应用举例

1.2.1 基本原理

数学模型法是将化工过程各变量之间的关系用一个（或一组）数学方程式来表示，通过对方程的求解可以获得所需的设计或操作参数。

按数学模型的由来，可将其分为机理模型和经验模型两大类。前者从过程机理推导得出，后者由经验数据归纳而成。习惯上，一般称前者为解析公式，后者为经验关联式。如流体力学中的泊谡叶（Poiseuille）公式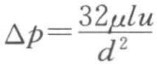：，即为流体在圆管中做层流流动的解析公式；而流体在圆管中湍流时摩擦系数的表达式，则为经验关联式。化学工程中应用的数学模型大都介于两者之间，即所谓的半经验半理论模型。本节所讨论的数学模型，主要指这种模型。机理模型是过程本质的反映，因此结果可以外推；而经验模型（关联式）来源于有限范围内实验数据的拟合，不宜于外推，尤其不宜于大幅度外推。在条件可能时还是希望建立机理模型。但由于化工过程一般都很复杂，再加上观测手段的不足、描述方法的有限，要完全掌握过程机理几乎是不可能的。这时，不得已提出一些假设，忽略一些影响因素，把实际过程简化为某种物理模型，通过对物理模型的数学描述建立过程的数学模型。

实际上，在解决工程问题时一般只要求数学模型满足有限的目的，而不是盲目追求模型的普遍性。因此，只要在一定的意义下模型与实际过程等效而不过于失真，该模型就是成功的。这就允许在建立数学模型时抓住过程的本质特征，而忽略一些次要因素的影响，从而使问题得到简化。过程的简化是建立数学模型的一个重要步骤，唯有简化才能解决复杂过程与有限手段的矛盾。科学的简化如同科学的抽象一样，都能深刻地反映过程的本质。从这一意义上说，建立过程的数学模型就是建立过程的简化物理图像的数学方程式。在过程的简化中，一般遵循下述原则：

（1）过程的本质特征和重要变量得以反映；

（2）应能适应现有的实验条件和数学手段，使得能够对模型进行检验，对参数能够估值；

（3）应能满足应用的需要。

一般地，所建立的数学模型含有若干模型参数，例如对代数模型

y＝f（x 1，x2，⋯ ，xn；b1，b2，⋯ ，bm）

其中x为自变量，即过程输入量；b为模型参数。

模型参数除极个别情况下可根据过程机理得到外，一般均为过程未知因素的综合反映，需通过实验确定。在建立模型的过程中要尽可能减少参数的数目，特别是要减少不能独立测定的参数，否则实验测定不易准确，参数估值困难，外推时误差可能很大。

1.2.2 建立数学模型的一般步骤

建立过程数学模型的一般步骤如下。

（1）对过程进行观测研究，概述过程的特征

根据有关基础理论知识对过程进行理性的分析。一是分析过程的物理本质，研究过程的特征；二是分析过程的影响因素，弄清哪些是重要变量必须考虑，哪些是次要变量一般考虑或者可以忽略。如有必要，辅之以少量的实验以加深对过程机理的认识和考虑变量的影响。变量分析可依第1.1节所介绍的方法，按物性变量、设备特征尺寸变量和操作变量三类找出所有变量。在此基础上，对过程物理本质做出高度概括。

（2）抓住过程特征做适当简化，建立过程物理模型

寻求对过程进行简化的基本思路是研究过程的特殊性，亦即过程物理本质的特征，然后做出适当假设，使过程得以简化，这是建立物理模型乃至数学模型最关键也是最困难的环节。要做到简化而不失真，既要有对过程的深刻理解，也要有一定的工程经验。所谓物理模型就是简化后过程的物理图像。所建立的数学模型必须要与实际过程等效，并且能够用现有的数学方法进行描述。

（3）根据物理模型建立数学方程式（组），即数学模型

用适当的数学方法对物理模型进行描述，即得到数学模型。数学模型是一个或一组数学方程式。对于稳态过程，数学模型是一个（组）代数方程式，对动态过程则是微分方程式（组）。对化工单元过程，所采用的数学关系式不外乎以下几种，即：

物料衡算方程；

能量衡算方程；

过程特征方程（如相平衡方程、过程速率方程、溶解度方程等）；

与过程相关的约束方程。

（4）组织实验、参数估值、检验并修正模型

模型中的参数须通过实验数据的拟合而确定，由此看出，在数学模型法中，实验目的不是为了直接寻求各变量之间的关系，而是通过少量的实验数据确定模型中的参数。

所建立的数学模型是否与实际过程等效，所做的简化是否合理，这些都需要通过实验加以验证。检验的方法有两种：一是从应用的目的出发，可从模型计算结果与实验数据（亦是工程应用范围）的吻合程度加以评判；二是适当外延，看模型预测结果与实验数据的吻合是否满意。如果两者偏离较大，超出工程应用允许的误差范围，须对模型进行修正。图1-2所示的是建立数学模型的工作程序框图。

图1-2 建立数学模型的程序框图

1.2.3 数学模型方法应用举例——流体通过固体颗粒床层的流动

在过滤、吸附等单元操作中，都涉及流体通过颗粒层流动的压降问题。流体通过颗粒层流动的复杂性在于流体通道几何形状不规则、纵横交联和曲折不定。如此复杂的流体通道几何边界和流体流动形态无法用严格的数学解析方法表述，所以解决流体在这些过程中的流动阻力问题，必须寻求有效的工程处理方法。

1.分析、概括过程的本质和特征

流体通过颗粒层的流动，就其流动过程本身来说是流体力学问题，这是过程的物理本质。问题的困难在于流体通道的复杂性。一般来说，构成颗粒床层的众多颗粒，不但颗粒大小不一、表面粗糙，而其几何形状也不规则，由这样的颗粒构成的流体通道，必然是不均匀的且纵横交联的网状通道。因此，不能直接利用流体在圆管中流动的有关公式计算流体通过颗粒床层的压降，必须根据过程的特征寻求简化的解决方法。

寻求简化途径的基本思路是研究过程的特殊性，即过程的特征，并充分利用特殊性对过程做出有效的简化。

不难想象，通过颗粒层的流体可以有两个极限，一是高速流动，另一个是极慢流动。在高速流动时，流体阻力主要是形体阻力，与流速有关；极慢流动又称爬流，此时流体阻力主要来自流体的黏性力，阻力的大小一方面与流体接触的表面积，即颗粒的总表面积有关，另一方面与流体在颗粒间的真实流速有关。在一定流量下，这一真实流速取决于流体在颗粒床层中流通孔道的大小，即颗粒床层的空隙容积。

在过滤过程中，流体通过的颗粒床层一般是由微细颗粒构成的滤饼，因而流体流速通常是很慢的，这就是过程的特殊性，亦即过程的特征。(www.xing528.com)

基于以上几方面的分析和认识，可以设想，如果能对颗粒床层的总表面积和空隙容积做出恰当的描述，就可以回避流体通道几何形状的复杂性这一困难，从而可对过程做出大幅度简化。

2.适当简化，建立过程的物理模型

基于对过程的物理本质和特征的深刻认识，可以将流体通过颗粒床层的流动简化为流体通过一束虚拟管径为de的平行圆管的流动，并且假定：

（1）管路的内表面积等于床层颗粒的总表面积；

（2）管路的流动空间等于颗粒床层的空隙容积。

根据以上描述，即可建立起过程的物理模型，如图1-3所示。

3.对物理模型进行数学描述，建立数学模型

根据物理模型的两点假设，可以推导出虚拟细管的当量直径。

等表面积

LA（1－ε）a＝nπde·Le　（1-1）

图1-3 流体在颗粒床层中流动过程的物理模型

等空隙容积

式中　L——颗粒层高度；

A——床层截面积；

a——颗粒的比表面积；

Le——模型床层高度；

de——模型细管当量直径；

n——模型细管数。

以上两式相除，即得：

由于实际床层与模型床层具有相等的空隙容积，在一定流量下，流体在两个床层内的停留时间相等，即：

Le为虚拟圆管的长度，L与Le一般并不相等，但应有下述关系：

Le＝C·L 　（1-6）

因此，流体通过模型细管的流速为

对于已建立的物理模型，可以应用流体在圆管中流动的有关流体力学理论加以数学描述：

将式（1-3）、式（1-6）、式（1-7）代入式（1-8），可得

令，于是

4.数学模型的实验检验与参数估值

以上的理论分析是建立在流体力学的一般知识和过滤操作中极慢流动相结合的基础上的，也就是将过程的一般性和特殊性相结合。这正是多数工程问题处理方法的共同点。忽视流动的基本原理就会走向纯经验的处理方法；抓不住极慢流动的特点，就找不到简化的途径，导致烦琐的处理方法。

应当指出，上述的过程分析和建模工作应在系统地进行实验前完成。当然，为了认识过程的机理，把握过程的特征，必要时不排除在理论分析前做一些初期认识性的实验，这其中也包括采用前人已有的经验。

“实践是检验真理的唯一标准。”上述的理论分析是否合理，所建立的模型能否与实际过程相符合，必须通过实验来加以检验，同时利用实验数据定量地确定模型参数。如果实验结果与模型不符，必须进行必要的修正。

前人对颗粒床层中的流体流动压降已做了大量实验，发现在Re′＜2的情况下，

式中，K′称为Kozeny常数，其值为5.0；Re′为床层雷诺数：

对于各种不同的颗粒床层，模型计算结果与实验数据误差不超过10％，证明所建立的模型是恰当的。