量纲理论指导下的实验研究方法优化

1.1.1 问题的提出

在化工过程中，当对某一单元操作过程的机理没有足够的了解，且过程所涉及的变量较多时，人们可以暂时撇开对过程内部真实情况的剖析而将其作为一个“黑箱”，通过实验研究外部条件（输入）与过程结果（输出）之间的关系及其动态特征，以掌握该过程的规律，并据此探索过程的内部结构和机理。在实验研究方法理论中，这种方法也称为“黑箱”法。如上所述，流体湍流流动过程可用图1-1所示的“黑箱模型”表示。

图1-1 研究湍流流动阻力的“黑箱模型”

实验研究的任务是要找出：hf＝f（u，d，l，ε，ρ，μ）的函数形式及式中的有关参数。

在“黑箱”法中，过程的输入变量必须是可控的，过程的输出结果必须是可测的。然而，正如前面所讲，用直接实验方法研究流体流动阻力将面临实验工作量很大和实验难以组织（例如无法分别改变ρ，μ）的困难，而量纲分析理论指导下的实验研究方法则可以轻而易举地解决这种困难，并能达到“由此及彼”“由小见大”的功效。

1.1.2 量纲分析理论

1.几个基本概念

（1）基本物理量、导出物理量

流体流动问题在物理上属于力学领域问题，在力学领域中，通常规定长度l、时间t和质量m这三个物理量为基本物理量，其他力学物理量，如速度u、压力p等可以通过相应的物理定义或定律导出，称为导出物理量。

（2）量纲、基本量纲、导出量纲、量纲一准数（量纲一数群）

量纲（Dimension）它是物理量的表示符号，如以[L]、[T]、[M]分别表示长度、时间和质量，则[L]、[T]、[M]分别称为长度、时间和质量的量纲。

基本量纲基本物理量的量纲称为基本量纲，力学中习惯上规定[L]、[T]、[M]为三个基本量纲。

导出量纲 顾名思义，导出物理量的量纲称为导出量纲，导出量纲可根据物理定义或定律由基本量纲组合表示，例如：

量纲一准数 又称量纲一数群，由若干个物理量可以组合得到一个复合物理量，组合的结果是该复合物理量关于基本量纲的指数均为零，则称该复合物理量为一量纲一准数，或称量纲一数群。如流体力学中的雷诺数：

2.几个重要的定理

1）物理方程的量纲一致性定理

对于任何一个完整的物理方程，不但方程两边的数值要相等，等式两边的量纲也必须一致。此即为物理方程的量纲一致性定理或称量纲一致性原则。物理方程的量纲一致性原则是量纲分析方法的重要理论基础。

如物理学中的自由落体运动公式：

等式左边s表示自由落体的距离，其量纲为[L]，等式右边第一项的量纲为[LT﹣1][T]＝[L]，第二项的量纲为[LT﹣2][T2]＝[L]，由此可见，方程两边的量纲是一致的。

此外，在化学工程中还广泛应用着一些经验公式，这些公式两边的量纲未必一致，在具体应用时应特别注意其中各物理量的单位和公式的应用范围。

2）π定理（Buckingham定理）

如果在某一物理过程中共有n个变量x1，x2，⋯，xn，则它们之间的关系原则上可用以下函数式表示：

f1（x1，x2，⋯ ，xn）＝0

如果规定了m个基本变量，则根据量纲一致性原则可将这些物理量组合成（n－m）个量纲一准数π1，π2，⋯，πn－m，则这些物理量之间的函数关系可用如下的（n－m）个量纲一准数之间的函数关系来表示：

f 2（π1，π2，⋯ ，πn－m）＝0

此即为Buckingham的π定理。π定理可以从数学上得到证明。

在应用π定理时，基本变量的选择要遵循以下原则：

（1）基本变量的数目要与基本量纲的数目相等；

（2）每一个基本量纲必须至少在此m个基本变量之一中出现；

（3）此m个基本变量的任何组合均不能构成量纲一准数。

3）相似定理

（1）相似的物理现象具有数值相等的相似准数（即量纲一准数）。

（2）任何物理现象的诸变量之间的关系，均可表示成相似准数之间的函数。

（3）当诸物理现象的等值条件（即约束条件）相似，而且由单值条件所构成的决定性准数的数值相等时，这些现象就相似。

以上也称为相似三定理。需要说明的是，相似准数有决定性和非决定性之分，决定性准数由单值条件所组成，若准数中含有待求的变量，则该准数即为非决定性准数。

准数函数最终是何种形式，量纲分析法无法给出。基于大量的工程经验，最为简便的方法是采用幂函数的形式，例如，流体流动阻力的量纲一准数关联式的形式为

式中，，称为欧拉准数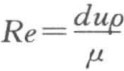；，称为雷诺准数或流体运动准数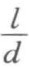；，称为几何相似准数。

其中常数C和指数a，b均为待定系数，须由实验数据拟合确定。

设有两种不同的流体在大小、长短不同的两根圆管中做稳定流动，且知此两种流动现象彼此相似。若令A和B分别表示这两种现象，则按相似第一定理，有

反之，对于流动现象A和B，分别以准数函数式表示：

若ReA＝ReB和，依相似第（3）定律，则A和B必为相似现象，且有

EuA＝EuB

相似定理在没有化学变化的化工工艺过程和装置的放大设计中有重要的作用，是工业装置经验放大设计的重要依据，一般，也称这种经验放大方法为相似放大。

1.1.3 量纲分析法

利用量纲分析理论建立变量的量纲一准数函数关系的一般步骤如下所述。

（1）变量分析：通过对过程的分析，从三个方面找出对物理过程有影响的所有变量，即物性变量、设备特征变量、操作变量，加上一个因变量，设共有n个变量x1，x2，⋯，xn，写出一般函数关系式：

F1（x1，x2，⋯，xn）＝0

（2）指定m个基本量纲，对于流体力学问题，习惯上指定[M]、[L]、[T]为基本量纲，即

m＝3

（3）根据基本量纲写出所有各基本物理量和导出物理量的量纲。

（4）在n个变量中选定m个基本变量。

（5）根据π定理，列写出（n－m）个量纲一准数

其中xA、xB、xC为选定的m（＝3）个基本变量，xi为除去xA、xB、xC之后所余下的（n－m）个变量中之任何一个，a、b、c为待定指数。

（6）将各变量的量纲代入量纲一准数表达式，依照量纲一致性原则，可以列出各量纲一准数的关于各基本量纲的指数的线性方程组，求解这（n－m）个线性方程组，可求得各量纲一准数中的待定系数a，b，c，从而得到各量纲一准数的具体表达式。

（7）将原来几个变量间的关系式F1（x1，x2，⋯，xn）＝0改以（n－m）个量纲一准数之间的函数关系表达式：

F2（π1，π2，⋯，πn－m）＝0

以函数F2中的量纲一准数作为新的变量组织实验，通过对实验数据的拟合求得函数F2的具体形式。

由此可以看到，利用量纲分析法可将n个变量之间的关系转变为（n－m）个新的复合变量（即量纲一准数）之间的关系。这在通过实验处理工程实际问题时，不但可使实验变量的数目减少，使实验工作量大幅度降低，而且还可通过变量之间关系的改变使原来难以进行或根本无法进行的实验得以容易实现。因此，把通过量纲分析理论指导组织实施实验的研究方法称为量纲理论指导下的实验研究方法。

1.1.4 量纲分析法应用举例

有一空气管路直径为300mm，管路内安装一孔径为150mm的孔板，管内空气的温度为200℃，压力为常压，最大气速为10m/s，试估计空气通过孔板的阻力损失为多少？(www.xing528.com)

为了测定工业高温空气管路中孔板在最大气速下的阻力损失，可在实验室中采用直径为30mm的水管进行模拟实验。现在需要解决的问题是：（1）在实验装置管路中模拟孔板的孔径应为多大？（2）若实验水温为20℃，则水的流速应为多少才能使实验结果与工业情况相吻合？（3）如实验测得模拟孔板的阻力损失为20mmHg[1]，那么工业管路中孔板的阻力损失为多少？

下面采用量纲分析法解决这一工程问题。

解：（1）变量分析

根据有关流体力学的基础理论知识，按物性变量、设备特征尺寸变量和操作变量三大类找出影响孔板阻力hf的所有变量。

物性变量：流体密度ρ，黏度μ；

设备特征尺寸：管径d，孔板孔径d0；

操作变量：流体流速u。

应说明的是，流体的温度亦是一操作变量，但温度的影响已隐含在流体的物性中（ρ和μ均为温度的函数），因而不再将温度视为独立变量，故在变量分析时不再计入。

因此hf＝f（ρ，μ，d，d0，u）

或f′＝（hf，ρ，μ，d，d0，u）＝0

（2）指定m个基本量纲

基本量纲为[M]、[L]、[T]，故m＝3。

（3）根据基本量纲写出各变量的量纲

（4）在n个变量中选定m个基本变量

总变量数n＝6，m＝3，可选择ρ、d、u为基本变量，该变量组合符合π定理中的规定。

（5）根据π定理，列出n－m＝6－3＝3个量纲一准数，即

（6）将各变量量纲代入量纲一准数表达式，并按量纲一致性原则，列出各量纲一准数关于基本量纲指数的线性方程，并解之。

对π1，有

可得

[M]：0＝a1

[L]：0＝2－3a1＋b1＋c1

[T]：0＝﹣2－c1

解上述线性方程组得：

将a1、b1、c1代入π1表达式得

π1＝hfu﹣2＝hf/u2

对π2，有

可得

[M]：0＝a2

[L] ：0＝1－3a2＋b2＋c2

[T]：0＝﹣c2

解上述线性方程组得

将a2、b2、c2代入 π2表达式得

[π2]＝d0d﹣1＝d0/d

对π3，有

可得

[M]：0＝1＋a3

[L]：0＝﹣1－3a3＋b3＋c3

[T]：0＝﹣1－c3

解上述线性方程组得

所以

或

（7）根据上述结果，可将原来变量间的函数关系f′（hf，ρ，μ，d，d0，u）＝0简化为

又可表示为

按此式组织模拟实验。注意到在上述量纲分析过程中并没有注明流体是气体还是水。因此，不论是气体管路还是水管，只要d0/d和Re相等，根据相似定理，方程左边hf/u2必相等。

按相似定理，模拟实验管路的孔板直径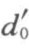应与实际气体管路孔板保持几何相似：

水的流速大小应保证实验管路中的Re与实际管路相等，即流体流动形态相似：

空气的物性：

μ＝2.6×10﹣5Pa·s

20℃水的物性：

ρ′＝1000（kg/m3）

μ′＝1×10﹣3Pa·s

代入上述相似式后，得水的流速为

模拟孔板的阻力损失：

实际孔板的阻力损失应与模拟孔板有如下关系：

所以

从这个例子可以看出，用量纲分析法处理工程问题，不需要对过程机理有深刻全面的了解。在该例中，原来hf与5个变量之间的复杂关系通过量纲分析法被简化为hf/u2与两个量纲一组合变量之间的函数关系，使得实验工作量大为减少，简化了实验。由于在模拟实验中保持了d0/d和duρ/μ与实际管路相等，因此可用常温下的水代替200℃的高温空气，用30mm的水管代替300mm的空气管道来进行实验。在实验物料上做到了“由此及彼”，在设备尺寸上达到了“由小见大”，实验结果解决了工业实际问题。

此外，应用量纲分析法，还解决了一般实验方法对于某些变量无法组织实验的困难。例如在该例中，如要分别考察ρ、μ对流动过程的影响，由于ρ、μ同时受温度的影响而变化，其实验难度之大是难以想象的。而由于ρ、μ、d和u共组于量纲一数群Re中，所以，无需想方设法改变ρ和μ，只需简单地调节u使Re改变即可，这是其他实验方法所不具备的独特优点。

应该指出的是，虽然量纲理论指导下的实验方法有上述诸多优点，但由于量纲分析法在处理工程问题时不涉及过程的机理，对影响过程的变量亦无轻重之分，因此，实验研究结果只能给出实验数据的关联式，而无法对各种变量尤其是重要变量对过程的影响规律进行分析判断。当过程比较复杂时，无法对过程的控制步骤或某些控制因素给出定量甚至是定性的描述。从根本上说，这种实验方法还是一种“黑箱”方法，其实验结果的应用仅限于实验范围，若将实验范围外延，其误差是难以预测的。此外，在分析过程的影响变量时，有可能漏掉重要的变量而使结果不能反映工程实际情况，也有可能把关系不大的变量考虑进来而使得问题复杂化。解决这一困难的途径除了要有扎实的基础理论知识外，掌握一定的工程经验也是十分重要的。

[1] 1mmHg＝133.322Pa。