史密斯预估补偿法的仿真分析优化

【例6-14】史密斯预估补偿法仿真分析仪。

史密斯预估补偿法仿真分析仪程序如shixz06_14所示。前面板和程序框图面板分别如图6-7-2和图6-7-3所示。

（1）前面板赋值及被控对象离散化模型

参见图6-7-3。用户在前面板上设置不超过5阶且不含延迟的连续被控对象。在“设定参数”控件簇内设置采样周期T，延迟时间tao和仿真拍数n_k。在“积分系数”控件中设置积分系数K_i。离散化程序段如下：

实例运行后被控对象连续模型（g0）

被控对象离散模型（gz1zp）

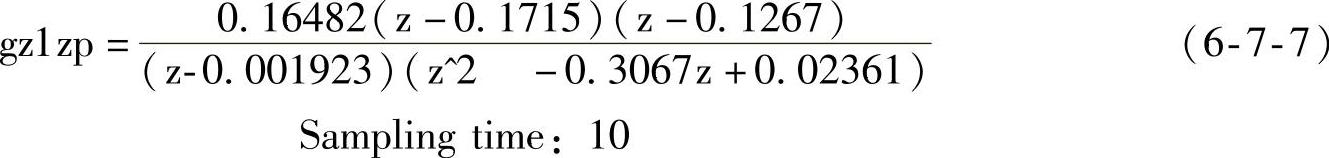
（2）常规PID调节器D（z）设计程序段

详见程序shixz06_12，不同之处在于由用户在前面板上设定积分常数K_i、程序计算比例系数K_p和微分系数K_d，只需两个相关方程。常规PID调节器（Dzzp）

显然，调节器Dzzp的两个零点抵消了被控对象构造gz1zp的两个极点。前已述及，积分常数K_i的数值对控制性能影响很大，仿真时应当从较小的数值逐渐调大。

图6-7-2 程序shixz06_14前面板图

（3）构造史密斯预估调节器式（6-7-3）的程序段(www.xing528.com)

注意程序中n0和n01的作用。运行得

图6-7-3 程序shixz06_14框图面板

含预估器的调节器（Dzb）数据示于前面板左下角的簇中，非最简约形式。

（4）研究图6-7-2两个示波器的曲线可以发现，系统的输出响应从第3拍开始，控制信号从第0拍开始，系统响应有延迟，调节器输出由于预估器的存在而补偿了这种延迟。

（5）积分系数对系统控制性能的强烈影响

将被控对象改变为

当其余参数保持不变时，控制系统不稳定，单位阶跃响应如图6-7-4a所示。在仿真仪连续运行模式下，不断减小积分系数K_i，系统将逐渐离开不稳定状态，当K_i=0.35时，系统单位阶跃响应如图6-7-4b所示。对比可知，积分系数K_i在PID调节器中的重要作用。

顺便提及，史密斯预估补偿法对系统参数变化的适应能力较强，读者可在仿真仪上进行研究。

图6-7-4 积分系数K_i对调节器控制性能的影响

程序shixz06-14a示出了使用阶梯波显示曲线的史密斯预估器算法，可供参考。